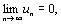- •Билет 1 Дифференциальные уравнения первого порядка
- •Дифференциальные уравнения первого порядка.
- •Доказательство единственности решения
- •Билет 2 Дифференциальные уравнения с разделяющимися переменными
- •Однородные уравнения первого порядка.
- •§ 6. Линейное уравнение первого порядка
- •1 Случай.
- •Метод решения Первый способ
- •Второй способ
- •§ 7. Уравнение в полных дифференциалах
- •Определение
- •Сходимость числовых рядов
- •Необходимый признак сходимости ряда
- •Радикальный признак Коши
- •Предельная форма
- •Доказательство
- •Примеры
- •Интегральный признак Коши
Предельная форма
Условие радикального признака равносильно следующему:
![]()
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
-
Если для ряда
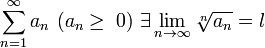 ,
то
,
тоесли
 ряд
сходится,
ряд
сходится,если l > 1 ряд расходится,
если l = 1 вопрос о сходимости ряда остается открытым.
Доказательство
1.
Пусть l <
1.
Очевидно, что существует такое ![]() ,
что l +
ε < 1.
Поскольку существует предел
,
что l +
ε < 1.
Поскольку существует предел ![]() ,
то подставив в определение предела
выбранное ε получим:
,
то подставив в определение предела
выбранное ε получим:
![]()
Раскрыв модуль, получаем:
![]()
![]()
(l − ε)n < an < (l + ε)n
Поскольку l +
ε < 1,
то ряд ![]() сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
сходится.
Следовательно, по признаку
сравнения ряд
тоже
сходится.
2. Пусть l > 1. Очевидно, что существует такое , что l − ε > 1. Поскольку существует предел , то подставив в определение предела выбранное ε получим:
Раскрыв модуль, получаем:
(l − ε)n < an < (l + ε)n
Поскольку l −
ε > 1,
то ряд ![]() расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
расходится.
Следовательно, по признаку
сравнения ряд
тоже
расходится.
Примеры
1. Ряд
![]()
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
![]()
2. Рассмотрим ряд
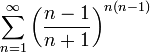
![]() ряд
сходится.
ряд
сходится.
Билет 20
Интегральный признак Коши
Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд
![]() сходится,
если сходится несобственный интеграл
сходится,
если сходится несобственный интеграл 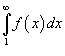 ,
и расходится, если
,
и расходится, если 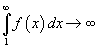 .
.
Пример
Определить, сходится или расходится
ряд 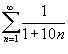 .
.
Решение.
Используем интегральный признак Коши.
Вычислим соответствующий несобственный
интеграл:  Таким
образом, данный ряд расходится.
Таким
образом, данный ряд расходится.
Пример
Показать, что обобщенный гармонический
ряд ![]() сходится
при p
> 1.
сходится
при p
> 1.
Решение.
Рассмотрим соответствующую функцию 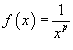 и
применим интегральный признак.
Несобственный интеграл равен
и
применим интегральный признак.
Несобственный интеграл равен  Видно,
что обобщенный гармонический ряд
сходится при значении p
> 1
Видно,
что обобщенный гармонический ряд
сходится при значении p
> 1
В зависимости от типа произведения применятся одна из трех формул:
![]()
![]()
![]()
Пример.
![]()
Пример.
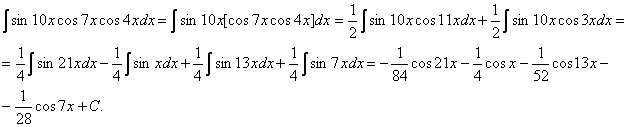
Определенный интеграл Основным методом решения задач, в которых требуется найти объем тела, ограниченного данной поверхностью, является введение соответствующих новых переменных, упрощающих интегрирование.
Билет 21.
Знакопеременные ряды |
Определение 5. Числовые ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными рядами. Ряды, все члены которых отрицательные числа, не представляют нового по сравнению со знакоположительными рядами, так как они получаются умножением знакоположительных рядов на –1. Изучение знакопеременных рядов начнём с частного случая – знакочередующихся рядов. Определение 6. Числовой ряд вида u1-u2+u3-u4+…+ +(-1)n-1.un+…, где un – модуль члена ряда, называется знакочередующимся числовым рядом.
Теорема 9. (Признак Лейбница) Если для знакочередующегося числового ряда
Выполняются два условия: Члены ряда убывают по модулю u1>u2>…>un>…,
то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Доказательство. Рассмотрим частичную сумму чётного числа членов ряда S2n=(u1-u2)+(u3-u4)+…+(u2n-1-u2n). По условию u1>u2>…>u2n-1>u2n, то есть все разности в скобках положительны, следовательно, S2n возрастает с возрастанием n и S2n>0 при любом n. С
другой
стороны S2n=u1-[(u2-u3)+(u4-u5)+…+(u2n-2-u2n-1)+u2n]. Выражение
в квадратных скобках положительно
и S2n>0,
поэтому S2n<u1 для
любого n.
Таким образом, последовательность
частичных сумм S2n возрастает
и ограничена, следовательно, существует
конечный Рассмотрим теперь частичную сумму нечётного числа членов ряда S2n+1=S2n+u2n+1. Перейдём в последнем равенстве к пределу при n→∞: S2n+1= S2n+ u2n+1=S+0=S. Таким образом, частичные суммы как чётного, так и нечётного числа членов ряда имеют один и тот же предел S, поэтому Sn=S, то есть данный ряд сходится. Теорема доказана.
Пример. Исследовать
на сходимость ряд Применим признак Лейбница. un=
un=
Оба условия признака Лейбница выполняются, следовательно, ряд сходится.
Замечания. 1. Теорема Лейбница справедлива и если условие un>un+1 выполняется, начиная с некоторого номера N. 2.
Условие un>un+1 не
является необходимым. Ряд может
сходиться, если оно не выполняется.
Например, ряд Определение 8. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин членов этого ряда, расходится, то говорят, что знакопеременный ряд сходится условно. Определение 9. Если сходится и сам знакопеременный ряд и ряд, составленный из абсолютных величин его членов, то говорят, что знакопеременный ряд сходится абсолютно. Пример. Установить
характер сходимости ряда Очевидно,
что данный ряд сходится по признаку
Лейбница. Действительно: Ряд,
составленный из абсолютных величин
членов данного ряда
Теорема 10. (Достаточный признак сходимости знакопеременного ряда или признак абсолютной сходимости) Пусть u1+u2+…+un+…= знакопеременный ряд и пусть сходится ряд, составленный из абсолютных величин его членов │u1│+│ u2│+…+│ un │+…= Тогда ряд (20) тоже сходится. Доказательство. Рассмотрим вспомогательный ряд (u1+│u1│)+(u2+│u2│)+…+(un+│un│)+…= Очевидно, 0≤ un+│un│≤2│un│ при всех n=1, 2, … . Ряд (21) сходится по условию, поэтому сходится ряд 2│un│, тогда по признаку сравнения сходится ряд (22). Ряд (20) представляет собой разность двух сходящихся рядов (22) и (21), поэтому он тоже сходится. Теорема доказана.
Замечание. Обратное утверждение неверно. Если данный ряд сходится, то ряд, составленный из абсолютных величин его членов, может и расходиться. Например,
ряд
Остаток ряда и его оценка Рассмотрим сходящийся числовой ряд
Вычисление
суммы ряда S= Определение 7. Если числовой ряд сходится, то разность Rn=S-Sn называется n-м остатком ряда. Таким образом, Rn представляет собой сходящийся числовой ряд: Rn= un+1+un+2+… . Заметим, что Rn= ( S-Sn)=S-S=0. Абсолютная погрешность при замене суммы ряда S его частичной суммой Sn равна |Rn|=|S-Sn|. Таким образом, если требуется найти сумму ряда с точностью до E>0, то надо взять сумму такого числа n первых членов ряда, чтобы выполнялось условие |Rn|<E. Однако в общем случае находить точноRn не удаётся.
Теорема 11. (Об оценке остатка знакочередующегося числового ряда) Если знакочередующийся числовой ряд сходится по признаку Лейбница, то его n-й остаток по абсолютной величине не превосходит модуля (n+1)-го члена ряда. Доказательство. Пусть ряд u1-u2+u3-u4+…+(-1)n-1.un+… сходится по признаку Лейбница. Тогда n-й остаток ряда Rn=±(un+1-un+2+un+3-…) сам является суммой знакочередующегося числового ряда и по теореме Лейбница |Rn|≤|un+1|. Теорема доказана.
Пример. Вычислить
с точностью до 0,01 сумму ряда Очевидно,
ряд сходится по признаку
Лейбница. u1= |