Примеры задач линейного программирования и их математическая формулировка. 2

Общая постановка задачи линейного программирования. 3

Графический метод решения задачи линейного программирования. 5

Алгоритмический метод. 6

Введение в симплексный алгоритм. 6

Область применимости. 7

Свойство сходимости. 9

Табличное представление. 13

Матричное представление 14

ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 15

Анализ чувствительности решения 17

Примеры задач линейного программирования и их математическая формулировка.

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах  -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств. Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

Математическая формулировка.

Нужно определить максимум линейной целевой функции (линейной формы)

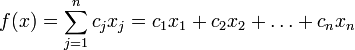
при условиях

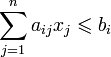 при  .

Иногда на   также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя её во всех остальных равенствах и неравенствах (а также в функции  ).

Такую задачу называют «основной» или «стандартной» в линейном программировании.

Транспортная задача.

Имеется некий однородный груз, который нужно перевести с   складов на   заводов. Для каждого склада   известно, сколько в нём находится груза  , а для каждого завода известна его потребность   в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния   от  -го склада до  -го завода известны). Требуется составить наиболее дешёвый план перевозки.

Решающими переменными в данном случае являются   — количества груза, перевезённого из  -го склада на  -й завод. Они удовлетворяют ограничениям:

Целевая функция имеет вид:  , которую надо минимизировать.

Максимальное паросочетание.

Рассмотрим задачу о максимальном паросочетании в двудольном графе: есть несколько юношей и девушек, причём для каждых юноши и девушки известно, симпатичны ли они друг другу. Нужно поженить максимальное число пар со взаимной симпатией.

Введём переменные  , которые соответствуют паре из  -того юноши и  -той девушки и удовлетворяют ограничениям:

с целевой функцией  . Можно показать, что среди оптимальных решений этой задачи найдётся целочисленное. Переменные, равные 1, будут соответствовать парам, которые следует поженить.

Общая постановка задачи линейного программирования.

Любое предприятие производит продукты, затрачивая ресурсы. Продукт  результат производства, то, что  выходит из производства. Это может быть материальный продукт (хлеб, машина, кирпич, дом, книга, видеокассета), либо услуга (транспортная, парикмахерская, предоставление в аренду жилья). Ресурс – то, что используется в производстве (труд, земля, сырье, техника). Причем ресурс  это не сам человек, земля или машина, а время использования их в производстве. Продукты и ресурсы в совокупности называются ингредиентами, под которыми понимается все, что имеет отношение к производству: ресурсы входят в производство, затрачиваются, продукты выходят из производства, создаются, порождаются.

Технологический способ – это обособленная, выделенная часть производства, использующая определенные ресурсы и производящая определенные продукты. Каждый технологический способ имеет идентификатор (имя или номер) и единицу измерения его мощности (интенсивности). Технологическим способом может быть отдельная технологическая линия, напр., конвейер по сборке автомашин, но это необязательно. Универсальное оборудование может выпускать различную продукцию, тогда технологическим способом будет производство на данном оборудовании какого-либо продукта, или целой группы продуктов, если они производятся вместе.

С каждым технологическим способом связан интерес человека, занятого планированием. Две противоположные постановки проблемы планирования:

а) при заданном наличии ресурсов произвести как можно больше продукции;

б) произвести заданное количество продуктов при наименьшем расходе ресурсов.

В просторечии задачу производства иногда формулируют следующим образом: произвести как можно больше продукции при наименьшем расходе ресурсов (максимизировать продукцию при минимальных издержках). Такая постановка проблемы невозможна, т. к. можно максимизировать или минимизировать только одну величину при ограничениях на остальные.

Введем обозначения:

j=1,…, n – номер технологического способа, его идентификатор;

i =1,…, m – номер ингредиента;

i=1,…, k  номер продукта, номера от единицы до k  присваиваем продуктам;

i = k + 1,…, m – номер ресурса,  ресурсам присваиваем номера от  k+1 до m;

a_ij  технологический коэффициент i-го ингредиента при единичной интенсивности использования j-го технологического способа;

a_ij при I ≤ k – выход( производство) i-го продукта при единичной интенсивности  j-го технологического способа;

a_ij при i > k – расход i-го ресурса при единичной  интенсивности использования j-го технологического способа;

b_i    ограничение на величину i-го ингредиента;

b_i при i≤ k - минимально допустимый объем производства i-го продукта; если такого ограничения нет, то b_i = 0;

b_i  при i > k - максимально допустимое значение расхода i-го ресурса; если такого ограничения нет, то b_i = ∞;

c_j  –  показатель качества плана при единичной интенсивности использования j-го технологического способа; это может быть обьем производства одного из продуктов, который нужно максимизировать, либо расход одного из ресурсов, который нужно минимизировать; это могут быть другие показатели, напр., выпуск продукции или прибыль (их нужно максимизировать) или издержки (необходимо минимизировать);

x_j – плановая интенсивность использования j-го технологического способа (переменная, неизвестная величина) .

           Условия задачи удобно записать в виде матрицы (рис. 4.3)

Приступим к созданию математической модели. Для определенности будем считать, что c_j   выпуск продукции в денежном выражении, который, естественно, нужно максимизировать. Будем последовательно собирать модель из элементов:

c_jx_j    плановый выпуск продукции j-м способом;

 –  плановый выпуск продукции в совокупности всеми способами; само выражение называется целевой функцией и ее нужно максимизировать; численная величина целевой функции называется критерием оптимальности;

a_ijx_j   плановая величина i-го ингредиента;

a_ijx_j при i ≤ k – плановый выпуск i-го продукта j-м способом;

 при i ≤ k - плановый выпуск i-го продукта всеми способами;

 при i ≤ k - нижняя граница выпуска i-го продукта; напомним, что если такого ограничения нет, то b_i = 0;

a_ijx_j  при i > k – плановый расход i- го ресурса j-м способом;

  при i > k - плановый расход i-го ресурса всеми способами;

    при i > k - ограничение по расходу i-го ресурса (нельзя израсходовать больше b_i).

Видно, что ограничения по продуктам (не меньше) и по ресурсам (не больше) имеют противоположный смысл. С целью упрощения записи желательно привести ограничения к одному виду. Для этого обе части ограничения по продуктам умножим на -1, а знак отношения сменим на противоположный (“не больше” заменим на “не меньше”).

Последнее ограничение – величина x_j не может быть отрицательной. Технологический способ либо используется, и тогда x_j > 0, либо нет, и тогда x_j= 0. Если же допустить, что x_j < 0, это означало бы, что технологический способ работает в обратном направлении. Напр., вместо производства бензина, керосина, мазута и других продуктов будет создаваться нефть из нефтепродуктов. В большинстве случаев это технически невозможно и в любом случае  экономически нецелесообразно.

Запишем математическую модель общей задачи линейного программирования.

Найти max при ограничениях:

  

        x_j ≥ 0.

Обратим внимание на то, что данную постановку задачи можно легко превратить в противоположную. Умножив на -1 целевую фукцию и ограничения по ингредиентам, получим.

Найти  min при ограничениях:

     

      x_j ≥ 0.

Обе постановки задачи эквивалентны. Модель составлена так, что на каждый ингредиент i имеется одно и только одно ограничение.

Может случиться так, что не по каждому ингредиенту (продукту или ресурсу) устанавливается ограничение. С другой стороны, по некоторым ингредиентам могут быть два ограничения  сверху и снизу. Пусть b_i  плановая величина i-го ингредиента ,  – нижняя допустимая граница значения b_i, а  верхняя граница. Тогда количество ограничений по таким ингредиентам удвоится:

Для общности будем считать, что всегда есть нижняя  и верхняя границы. По умолчанию = 0, а = ∞. В каждом конкретном решении значения  и уточняются.

Вектор ( x₁,…,x_j,…,x_n ) называется планом. Любой план, удовлетворяющий ограничениям, называется допустимым. При решении модели могут возникнуть три случая:

1) нет ни одного допустимого плана; в таком случае говорят,  что система ограничений несовместна, необходимо ослабить ограничения;

2) целевая функция не ограничена; это значит, что целевая функция несовместима с системой ограничений; необходимо пересмотреть модель, уточнив ограничения и целевую функцию;

3) система ограничений совместна и целевая функция на множестве допустимых решений ограничена; допустимый план, на котором целевая функция достигает экстремума (максимума или минимума в зависимости от постановки), называется оптимальным; оптимальных планов может быть множество ( более одного).