Табличное представление.

При переходе от одного пробного решения к следующему мы каж­дый раз выписывали все переменные x₁,x₂,…,x_n фигурирующие в рассматриваемой модели. Однако это, с одной стороны, громоздко, а с другой — не вызвано никакой необходимостью, поскольку в про­цессе вычисления используются лишь коэффициенты при незави­симых переменных. Теперь, когда понятна простая логика симплекс­ного алгоритма, объем сопутствующих записей можно существенно сократить, если весь вычислительный процесс представить в виде удобной таблицы, известной под названием симплекс-таблицы. Таблицы 3.9 и 3.10 представляют собой описание двух различных подходов к решению задачи, приведенной в разделе 3.4. В таблице 3.9. столбцы, соответствующие базисным переменным, имеют настолько тривиаль­ный смысл, что их без ущерба для однозначности понимания можно из упомянутой таблицы исключить. В результате получаем редуци­рованный вариант табличной записи, приведенный в таблице3.10. В этом случае после каждой итерации необходимо вводить одну допол­нительную строку, предназначенную для нового набора небазисных переменных.

Матричное представление

В данной главе, так же как и к следующей, при изложении сим­плексного метода и различных его модификаций каждое из уравне­ний модели записывается в явном виде. Если воспользоваться мат­ричными обозначениями, то математическая формулировка метода примет более компактный вид. Матричная запись линейной модели выглядит следующим образом:

Максимизировать сх (1)

при ограничениях:

Ax b (2)

x 0 (3)

В принятых обозначениях соответствующую симплекс-таблицу (4) на этапе первой итерации можно представить в виде

(4)

где- [⁰_Ui] — столбец с единицей на пересечении с i-й строкой и с нуля­ми на пересечении со всеми остальными строками. (Строке 0 в матри­це (4) принято отводить самую верхнюю позицию.) В еще более компактном виде вместо (4) будем иметь

(5)

где 0_pq — матрица с р строками и q столбцами, состоящая целиком из нулей, а I_т— m-мерная единичная матрица.

Выделим в (5) т столбцов, соответствующих пробному базису на этапе некоторой заданной итерации. Обозначим полученную таким образом матрицу через [ ^-C_B^B]. При этом первый столбец соответствует базисной переменной, фигурирующей в строке 1, второй столбец соответствует базисной переменной, фигурирующей в строке 2, и т. д. Тогда для данной итерации симплекс-таблица принимает следующий вид:

(6)

Нетрудно убедиться, что матрица (6) получена из матрицы (5) путем умножения последней слева на

= ^-1 (7)

Симплекс-критерий I (максимизация) сводится к нахождению наибольшего по модулю отрицательного матричного элемента в , т. е. в строке 0 матрицы (6). Предположим, что наибольший пo модулю отрицательный матричный элемент в соответствует х_j. Тогда, согласно крите­рию II, мы обращаемся в (6) к коэффициентам при х_j.

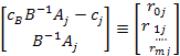(8)

Следует заметить, что если x_jпредставляет собой i-ю свободную переменную, то в (8) с_j =0 и Aj = U_j. Допустим, что выбор по критерию II падает на строку k. Последующая вычислительная про­цедура, связанная с заменой базиса, сводится к умножению матри­цы (6) слева на:

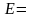
(9)

где отношения фигурируют в (k + 1)-м столбце матрицы Е. Умножение (6) на (9) часто называют операцией элементарного пре­образования.

Заметим, что значения для пробного базиса являются оптимальными, когда

(10)

Соответствующее значение целевой функции при этом равняется

(11)