Изменение координат вектора при переходе к новому базису

Пусть V – n-мерное линейное пространство, e и f  два его базиса, причем

f=Te. Пусть вектор а имеет в базисе e следующий вид:

а=₁e₁+₂e₂+…+_ne_n. (12)

Чтобы найти координаты вектора а в базисе f, перепишем соотношение (12) следующим образом:

a=(₁,₂.…._n) =(₁,₂.…._n) T^-1 ,

так как Т – матрица перехода от базиса e к базису f, то обратная ей матрица Т^-1 – матрица перехода от базиса f к базису е, то есть e=T^-1f. Таким образом,

a=((₁,₂.…._n) T^-1) f.

Чтобы получить координаты вектора а в базисе f, нужно строку координат вектора а в базисе е умножить на матрицу перехода от базиса f к базису е.

(₁’,₂’.…._n’) =(₁,₂.…._n) T^-1

§ 3. Линейные подпространства

Определение. Пусть V – линейное пространство, подмножество L множества V называется линейным подпространством пространства V, если оно образует линейное пространство относительно операций, определенных в V.

Замечание. Операции на подмножестве L индуцированы операциями на множестве V.

Примерами линейных подпространств любого пространства V могут служить так называемые «тривиальные» подпространства – {0} и V.

Теорема. Для того чтобы подмножество L линейного пространства V было линейным подпространством пространства V, необходимо и достаточно, чтобы выполнялись следующие условия:

1. a,bL(a+bL);

2. RaL(aL).

Доказательство  самостоятельно

Доказанная теорема позволяет построить пример линейного подпространства.

Пусть V – n-мерное линейное пространство и a₁,a₂,…,a_n  произвольная система векторов этого пространства. Рассмотрим всевозможные линейные комбинации этих векторов, выбрав в качестве коэффициентов действительные числа.

M={bb= _iR}

Очевидно, что MV и условия теоремы выполнены. Действительно

b,cM имеем b+c= + = M, аналогично

RbM имеем b=( )= M, следовательно, на основании доказанной теоремы можем утверждать, что M – линейное подпространство линейного пространства V.

Такое подпространство называется линейным подпространством, натянутым на векторы a₁,a₂,…,a_n, или подпространством, порожденным системой векторов a₁,a₂,…,a_n, или линейной оболочкой данной системы векторов.

Здесь следует обратить внимание на несколько очевидных, но очень важных фактов. В частности, на то, что размерность любого подпространства не превосходит размерности самого пространства, а размерность линейной оболочки системы векторов не превосходит числа векторов этой системы.

За размерность линейного пространства {0} будем принимать 0.

Действия над линейными подпространствами

Пусть L₁ и L₂  линейные подпространства линейного пространства V. По аналогии с теорией множеств можно рассмотреть операции над линейными подпространствами.

1. Пересечением линейных подпространств L₁ и L₂ называется множество

L₀={xx L₁xL₂}=L₁L₂.

Используя теорему о подпространстве, легко показать, что пересечение двух линейных подпространств линейного пространства V само является линейным подпространством линейного пространства V. Действительно, пусть

x,y L₀ xL₁xL₂ yL₁ y L₂x+yL₁x+ yL₂ x+ yL₀.

Аналогично,

пусть x L₀ и R  x L₁xL₂R x L₁xL₂ x L₀.

Оба условия теоремы выполнены, следовательно, L₀  линейное подпространство линейного пространства V.

2. суммой линейных подпространств L₁ и L₂ линейного пространства V называется множество

=L₁+L₂ ={xx=x₁+x₂ x₁ L₁x₂L₂}.

Если представление элементов множества как суммы элементов множеств L₁ и L₂ является однозначным, то сумма называется прямой и обозначается = L₁L₂.

Так как L₁V и L₂V, то, очевидно, V. Покажем, что  линейное подпространство линейного пространства V. Действительно, пусть

x,y  x=x₁+x₂ x₁ L₁x₂L₂ y=y₁+y₂ y₁ L₁y₂L₂

x+y=(x₁+x₂)+( y₁+y₂)=(x₁+y₁)+( x₂+y₂)  , так как x₁+y₁ L₁ x₂+y₂L₂.

Аналогично, пусть x  x=x₁+x₂ x₁ L₁x₂L₂ и пусть R, тогда

x₁ L₁x₂L₂ x=( x₁+x₂)= x₁+x₂ .

Оба условия теоремы выполнены, следовательно,  линейное подпространство линейного пространства V.

Примеры

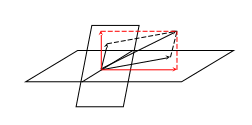
Пусть V – обычное трехмерное геометрическое пространство. L₁  множество векторов, лежащих в плоскости , L₂  множество векторов, лежащих в плоскости , причем , тогда L₁+L₂ совпадает с пространством V, причем эта сумма не будет прямой, что хорошо видно на примере.





Теорема. Размерность суммы линейных подпространств равна сумме их размерностей минус размерность пересечения, то есть

dim =dim(L₁+ L₂)=dimL₁+dimL₂-dim L₁ L₂

Доказательство

Пусть L₁ и L₂ – линейные подпространства линейного пространства V, обозначим dimL₁=m₁, dimL₂=m₂, L₀=L₁L₂, dimL₀=m₀, =L₁+ L₂, dim = и докажем, что = m₁+ m₂- m_0.

Рассмотрим базис пространства L₀ , он состоит из m₀ векторов:

e₁,e₂,…, (1)

Так как e₁,e₂,…,  L₀, то e₁,e₂,…, L₁ и e₁,e₂,…, L_{2 .}Дополним систему векторов (1) до базиса пространства L₁:

e₁,e₂,…, , … (2)

и до базиса пространства L₂:

e₁,e₂,…, , … (3)

По определению базиса,

aL₁₁,₂,…, , ,…, R(a=₁e₁+…+ +…+ ).

Аналогично

bL₁₁,₂,…, , ,…, R(b=₁e₁+…+ +…+ ).

Теперь рассмотрим линейное пространство

=L₁+L₂ ={xx=x₁+x₂ x₁ L₁x₂L₂},

тогда  x имеем x=a+b = =(₁e₁+…+ +…+ )+(₁e₁+…+ +…+ ) =

=(₁+₁)e₁+…+( + ) + + +…+ + + (4)

Из полученного соотношения (4) следует, что произвольный вектор линейного пространства является линейной комбинацией векторов

e₁,e₂,…, , … , … (5)

то есть линейное пространство является линейной оболочкой системы векторов (5). Покажем, что эта система векторов линейно независима.

Предположим противное. Пусть существуют такие действительные числа

₁, ₂,…, , ,…, , ,…, , что

₁e₁+…+ + +…+ + +…+ =0 (*)

и среди коэффициентов есть отличные от нуля.

Преобразуем последнее равенство

₁e₁+…+ =-( +…+ )=с, где с L₁, так как с=₁e₁+…+ является линейной комбинацией векторов базиса (2). Кроме того, с L₂, так как с=-( +…+ ) – линейная комбинация векторов линейного пространства L₂. Следовательно,

с L₀=L₁L₂, но тогда вектор с можно разложить по базису (1)

с=₁e₁+₂e₂+…+ =-( +…+ ).

Отсюда следует

₁e₁+₂e₂+…+ + +…+ =0,

так как это  линейная комбинация векторов базиса (3), то равенство нулю означает, что равны нулю все коэффициенты, то есть

₁=₂=…= = =…= =0  с=0₁e₁+…+ =0, а это линейная комбинация векторов базиса (2), и, следовательно, равенство нулю означает, что равны нулю все коэффициенты, то есть ₁=…= =0. Таким образом, мы получили, что равенство (*) возможно только в том случае, когда все коэффициенты равны нулю, а это, в свою очередь, означает, что система векторов (5) линейно независима. Поэтому система векторов (5) является базисом линейной оболочки , порожденной этими векторами. Число векторов в базисе (5) равно размерности линейного пространства и равно = m₁+ m₂- m₀, что и требовалось доказать.

Следствие. Размерность прямой суммы линейных подпространств равна сумме их размерностей.

Доказательство

Для доказательства достаточно показать, что = L₁L₂. L₁L₂ =0.

Действительно, если предположить противное, то есть найдется ненулевой вектор сL₁L₂, тогда сL₁ и сL₂ , следовательно, сL₁ и с L₂, сL₁ и с L₂, тогда с= с+ с= с+ с. Получили противоречие, L₁L₂ =0 и следствие доказано.