Глава IV. Линейные операторы в линейных пространствах § 1. Понятие линейного оператора. Матрица линейного оператора

Рассмотрим два линейных пространства:

V=(V,+,_) и V’=(V’,+,_).

Определение. Отображение  основного множества V в V’ называется линейным оператором (морфизмом) линейного пространства, если оно удовлетворяет условиям линейности:

1) a, b Va+b) (a)(b),

2) a V(aa).

Примеры

1. Всякий изоморфизм есть линейный оператор.

Ранее рассматривали изоморфное отображение V V’. Легко видеть, что всякий изоморфизм есть линейный оператор.

2. Построим отображение : V V’ следующим образом:

a Va) 0’.

Очевидно, что построенное отображение является линейным оператором.

3. Построим отображение : V V следующим образом:

a Va) а.

построенное отображение является линейным оператором.

4. Построим отображение : V V следующим образом:

a Va) -а.

построенное отображение является линейным оператором.

5. Рассмотрим линейное пространство

Построим отображение : V V:

фиксируем некоторую матрицу L= и образом произвольной матрицы АV будем считать матрицу (A)=LA.

Проверим выполнимость условий линейности.

1. Пусть ()LA, (B)LB, тогда (A+B)L(A+B)=LA+LB=()().

2. Пусть ()LA, тогда

( L =L =LA)= ().

Простейшие свойства линейных операторов

1. ()V.

2.  (-а) =-(а).

3. (₁a₁+...+_ka_k) = ₁(a₁) + ... + _k (a_k).

Доказать самостоятельно.

Матрица линейного оператора

Пусть V⁽ⁿ⁾ и V^(m)  конечномерные линейные пространства. (Будем в этой главе рассматривать только конечномерные линейные пространства.)

Обозначим базис пространства V⁽ⁿ⁾: (e)=(e₁, e₂,..., e_n), базис пространства V^(m): (f)=(f₁, f₂,..., f_m ).

Теорема (о матрице линейного оператора) Пусть V⁽ⁿ⁾ и V^(m)  конечномерные линейные пространства, пусть в пространстве V^(m) зафиксирована система векторов c₁, c₂,..., c_n V^(m), тогда существует единственный линейный оператор V⁽ⁿ⁾ в V^(m), обладающий свойством

(e₁)c₁  (e₂) c₂ ,..., (e_n)  c_n.

Доказательство

1. Докажем существование. Для этого достаточно построить линейный оператор, который удовлетворял бы условию теоремы. Рассмотрим произвольный вектор пространства V⁽ⁿ⁾ и разложим его по векторам базиса (e) : аV⁽ⁿ⁾___nа=_e₁_ e₂_n e_n. Очевидно, что аV⁽ⁿ⁾ (а)=_с₁_ с₂_n с_nV^(m). Так как а_ic_i определены однозначно по аксиоматике линейного пространства, тогда и (а) определен однозначно. А раз так, то  есть отображение v⁽ⁿ⁾v^(m). Покажем, что отображение  есть линейный оператор.

(а)=а₁с₁+...+а_nc_n

(b)=b₁с₁+...+b_nc_n

Если найдем в v⁽ⁿ⁾ сумму а+b, то это будет вектор а+b= =((а₁+b₁)е₁+...+(а_n+b_n) е_n), тогда его образ (а+b) =((а₁+b₁)с₁+...+(а_n+b_n) с_n)= =(а₁с₁+...+а_nc_n)+(b₁с₁+...+b_nc_n)= (а)+(b), тем самым сохранение операции сложения показано.

Сохранение операции умножения на действительное число доказывается аналогично.

(a) =(a₁)c₁+(a₂)c₂+...+a_n)c_n= a₁ c₁+ a₂c₂+...+a_nc_na.

Таким образом, построенное отображение  есть линейный оператор.

2. Покажем, что построенный линейный оператор  удовлетворяет условию теоремы. Найдем образы векторов базиса

e₁=1 e₁    e₂    e_n , следовательно, (e₁)=с₁

e₂=0 e₁  1 e₂    e_n , следовательно, (e₂)=с₂

................................................................................... ,

e_n=0 e₁    e₂  1 e_n , следовательно, (e_n)=с_n

то есть построенный линейный оператор  удовлетворяет условию теоремы.

3. Докажем, что такой оператор единственный. Предположим противное, что существует еще хотя бы один линейный оператор , который удовлетворяет всем остальным условиям теоремы, тогда

nV⁽ⁿ⁾( (a)  ₁e₁  ₂e₂  _ne_n)  ₁  (e₁)  ₂  (e₂   _n e_n  ₁c₁+ +₂c₂  _nc_n=(a).

Таким образом, любому вектору пространства V⁽ⁿ⁾ оба оператора сопоставляют один и тот же вектор  образ (a)(a).

Теорема доказана.

Доказанная теорема позволяет ввести понятие матрицы линейного оператора. Рассматриваются два линейных пространства V⁽ⁿ⁾ и V^(m). В пространстве V⁽ⁿ⁾ выбран базис (e) и в пространстве V^(m) выбран базис (, в пространстве V^(m) взята система векторов c₁, c₂,..., c_n, было доказано, что существует единственный линейный оператор из V⁽ⁿ⁾ в V^(m), отображающий векторы базиса (e) в векторы c₁, c₂,..., c_n. Но векторы c₁, c₂,..., c_nV^(m), следовательно, раскладываются по базису (, то есть имеем

c₁=₁₁₁₁₂₂_1m_m

c₂=₂₁₁₂₂₂_2m_m

...................................... .

c_n=_n1₁_n2₂_nm_m

Коэффициенты _ij образуют прямоугольную матрицу из n строк и m столбцов, причем такая матрица при перечисленных выше условиях определяется однозначно. Таким образом, мы можем говорить о взаимно-однозначном соответствии между множеством всех линейных операторов из V⁽ⁿ⁾ в V^(m), множеством систем векторов c₁, c₂,..., c_nV^(m) и множеством прямоугольных матриц А=(_ij )

.

Другими словами, из предположения о выборе фиксированных базисов в линейных пространствах V⁽ⁿ⁾ и V^(m) следует, что существуют биекции

Учитывая, что произведение биекций есть биекция, приходим к выводу, что существует биекция  множества операторов на множество прямоугольных матриц.

Из всего вышесказанного следует, что

,

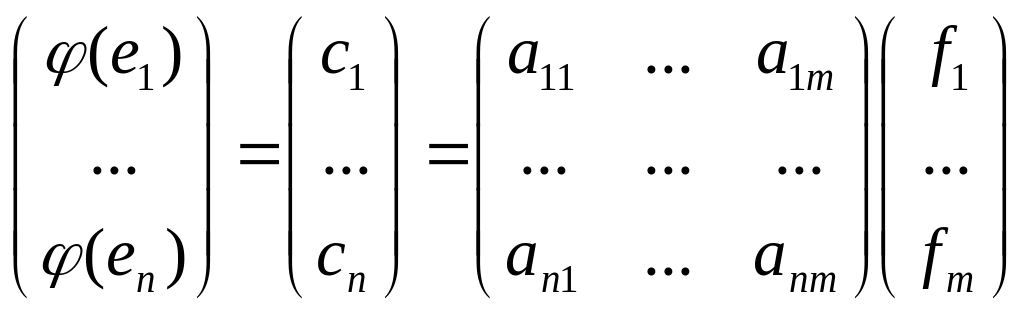то есть (e)A, где А  матрица линейного оператора.