Линейные операторы с простым спектром

Определение. Матрицу, все элементы которой, кроме элементов, стоящих на главной диагонали, равны 0, будем называть диагональной. То есть диагональная матрица имеет вид

.

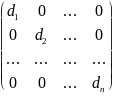Пусть   линейный оператор, отображающий V⁽ⁿ⁾V⁽ⁿ⁾. Пусть А  матрица линейного оператора  в некотором базисе (е). Известно, что при переходе от одного базиса линейного пространства V⁽ⁿ⁾ к другому базису этого же пространства матрица линейного оператора изменяется. Возникает вопрос, можно ли подобрать базис линейного пространства так, чтобы матрица линейного оператора имела в этом базисе диагональную форму? Ответ на этот вопрос дает следующая теорема.

Теорема. матрица линейного оператора  имеет в базисе (е) имеет диагональную форму, тогда и только тогда, когда каждый вектор этого базиса есть собственный вектор этого линейного оператора.

Доказательство

1. Пусть каждый вектор базиса (е) есть собственный вектор линейного оператора , тогда по определению имеем

j(e₁)= ₁ e₁ , j(e₂)= ₂ e₂, ..., j(e_n)= _n e_n.

Чтобы найти матрицу линейного оператора в базисе (е), разложим векторы j(e₁), j(e₂),..., j(e_n) по векторам базиса (е). Получим

(e₁) = ₁ e₁ + 0  e₂ + ...+ 0e_n

(e₂) = 0 e₁ + ₂ e₂ + ...+ 0e_n

................................................. .

(e_n) = 0 e₁ + 0  e₂ + ...+ _n e_n

Матрица линейного оператора  в базисе (е) имеет вид

.

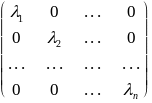2. Пусть линейный оператор  в базисе (е) задан матрицей А, имеющей диагональную форму:

А= .

Учитывая соотношение e=Ae, получим

(e₁) = ₁ e₁ + 0  e₂ + ...+ 0e_n

(e₂) = 0 e₁ + ₂ e₂ + ...+ 0e_n

................................................. .

(e_n) = 0 e₁ + 0  e₂ + ...+ _n e_n

Из полученных соотношений видно, что каждый вектор базиса (е) есть собственный вектор линейного оператора .

Теорема. Если в линейном пространстве V⁽ⁿ⁾ существует система собственных векторов b₁, b₂, ..., b_k, отвечающая различным действительным собственным значениям ₁, ₂, ..., _k, то система векторов b₁, b₂, ..., b_k  линейно независима.

Доказательство

Докажем методом математической индукции по числу векторов k.

1. Если k=1, то система состоит из одного ненулевого вектора b₁ и, следовательно, линейно независима.

2. предположим, что теорема верна для (k-1) вектора и рассмотрим систему векторов b₁, b₂, ..., b_k, которые удовлетворяют условию теоремы, то есть

(b₁)=₁b₁

(b₂)=₂b_{2 (*)}

............. .

(b_k)=_kb_k

Предположим, что система векторов b₁, b₂, ..., b_k линейно зависима, то есть существуют такие ₁__k , что ₁²  ₂²  ... +_k² 0, а

₁ b₁ +_ b₂ ++_k b_k =0. (1)

Используя свойства линейного оператора, найдем образ вектора

(₁ b₁ +_ b₂ ++_k b_k):

 (₁ b₁ +_ b₂ ++_k b_k) =(0)  ₁(b₁)+_(b₂) ++_k(b_k)=0.

Воспользовавшись соотношением (*), получим

(₁ ₁) b₁+(_ ₂ )b₂ ++(_k_k )b_k=0. (2)

Равенство (1) умножим на _k и вычтем из равенства (2), получим

₁ (₁ - _k) b₁ +_ (₂ - _k)b₂ ++_k-1 (_k-1 -_k )b_k-1=0. (3)

Так как все значения _i различны и среди коэффициентов _j есть отличные от нуля, тогда найдется значение _j (_j - _k)0, следовательно, система векторов b₁, b₂, ..., b_k-1 линейно зависима, что противоречит индуктивному предположению. Таким образом, система векторов b₁, b₂, ..., b_k линейно независима.

Следствие (достаточное условие приводимости матрицы линейного оператора к диагональному виду). Для того чтобы матрица линейного оператора имела диагональную форму, достаточно, чтобы линейный оператор имел простой спектр.