19) Характеристики н.С.В. Свойства матем.Ожидания и дисперсии н.С.В.
Пусть непрерывная сл. величина Х задана функцией распределения f(x). Допустим, что все возможные значения сл. величины принадлежат отрезку [a,b].
Мат.ожиданием непрерывной
случайной величины Х, возможные значения
которой принадлежат отрезку [a,b],
называется определенный интеграл
Если возможные значения сл. величины рассматриваются на всей числовой оси, то мат.кое ожидание находится по формуле:
При этом, конечно, предполагается, что несобственный интеграл сходится.
Свойства мат.ожидания н.с.в.
1. Мат. ожидание постоянной величины равно самой постоянной: . 2. Постоянный множитель можно вынести за знак мат. ожидания: . 3. Мат, ожидание произведения двух независимых сл.величин равно произведению их мат. ожиданий: . Следствие. Мат. ожидание произведения нескольких взаимно независимых случайных величин равно произведению их мат. ожиданий. 4. Мат.ожидание суммы двух сл.величин равно сумме мат.х ожиданий слагаемых: .
Дисперсией непрерывной сл.величины называется мат.жидание квадрата ее отклонения.
Для
практического вычисления дисперсии
используется формула:
Свойства дисперсии н.с.в.
1. Дисперсия постоянной величины равна нулю: . 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: . 3. Дисперсия суммы двух независимых случайных величин равно сумме дисперсий этих случайных величин: . Следствие. Дисперсия суммы нескольких взаимно независимых случайных величин равно сумме дисперсий этих величин. 4. Дисперсия разности двух независимых случайных величин равно сумме дисперсий этих случайных величин: .
Среднее
квадратическое отклонение
равно корню квадратному из дисперсии
:
20). Равномерное распределение .Плотность и функция распределения.
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).
Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероятности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.
Непрерывная
случайная величина Х имеет равномерное
распределение на отрезке [а,
в], если
на этом отрезке плотность распределения
вероятности случайной величины постоянна,
т. е. если дифференциальная функция
распределения f(х) имеет
следующий вид:
Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.
Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то
откуда с=1/(b-a).
Теперь функцию f(x) можно представить в виде
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:
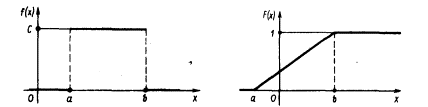
Графики
функций f(x)
и F(x)
имеют вид: