34) Основы математической статистики (примеры).

Мат. статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений.

Первая задача мат.статистики – указать способы получения, группировки и обработки стат. данных, собранных в результате наблюдений, поставленных опытов или произведённых измерений.

Вторая задача мат.статистики – разработка методов анализа статистических сведений в зависимости от целей исследования.

Например, целью исследования может быть:

- оценка неизвестной вероятности события;

- оценка параметров распределения сл.величины;

- оценка неизвестной функции распределения сл.величины;

- проверка гипотез о параметрах распределения или о виде неизвестного распределения;

- оценка зависимости сл.величины от одной или нескольких сл.величин и т.д.

Сл.величину   будем называть генеральной совокупностью  .

Исходным материалом для изучения свойств генеральной совокупности   являются стат. данные, т.е. значения  , полученные в результате повторения случайного опыта (измерения случайной величины  ). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение сл.величины  ,  , заданной на множестве исходов  -го опыта, не зависит от   и совпадает с распределением генеральной совокупности  .

Набор   независимых в совокупности сл.величин  , где   соответствует  -му опыту, называют случайной выборкой из генеральной совокупности  . Число   называется объёмом выборки.

Совокупность чисел  , полученных в результате  -кратного повторения опыта по измерению генеральной совокупности  , называется реализацией случайной выборки или просто выборкой объёма  .

В основе большинства результатов мат.статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности   устанавливаются путём изучения тех же свойств на случайной выборке.

Алгоритм построения интервального вариационного ряда.

1. Исходя из объема выборки n, определить количество интервалов k.

n	25-40	40-60	60-100	100-200	>200
k	5-6	6-8	7-10	8-12	10-15

2. Вычислить размах ряда: R=X_max-X_min

3. Определить ширину интервала: h=R/(k-1)

4. Найти начало первого интервала X₀ = X_min - h/2

5. Составить интервальный вариационный ряд.

Пример: измерена масса тела 100 женщин 30 лет, получены значения от 60 до 90 кг.

интервалы	60-65	65-70	70-75	75-80	80-85	85-90
количество	14	34	29	15	6	2

Размах ряда: R=X_max-X_min=90-60=30

Ширина интервала: h=R/(k-1)=30/5=6

Интервальный вариационный ряд:

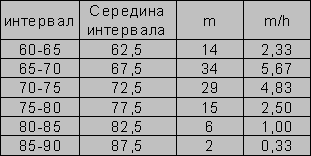
35).Статистические оценки неизвестных параметров распределения. Оценка мат.Ожидания и дисперсии.

Пусть изучается случайная величина Х с математическим ожиданием  и дисперсией , оба параметра неизвестны.

Пусть х1, х2, х3, …, хn – выборка, полученная в результате проведения n независимых наблюдений случайной величины Х. Чтобы подчеркнуть случайный характер величин х1, х2, х3, …, хn перепишем их в виде: Х1, Х2, Х3, …, Хn, где Хi – значение случайной величины Х в i-ом опыте.

Требуется на основании этих опытных данных оценить математическое ожидание и дисперсию случайной величины. Такие оценки называются точечными, в качестве оценки m и D можно принять статистическое математическое ожидание   и статистическую дисперсию  , где

, 

До проведения опыта выборка Х1, Х2, Х3, …, Хn есть совокупность независимых случайных величин, которые имеют математическое ожидание и дисперсию, а значит распределение вероятности такие же как и сама случайная величина Х. Таким образом:

, , где i = 1, 2, 3, …, n.

Исходя из этого, найдем математическое ожидание и дисперсию случайной величины  (пользуясь свойствами математического ожидания).

Таким образом математическое ожидание статистического среднего  равно точному значению математического ожидания m измеряемой величины, а дисперсия статистического среднего  в n раз меньше дисперсии отдельных результатов измерений.

при

Это значит, что при большом объеме выборки N статистическое средние   является величиной почти неслучайной, оно лишь незначительно отклоняется от точного значения случайной величины m. Этот закон называется законом больших чисел Чебышева.