Билет №29

Вопрос 1

Функция f(x) называется бесконечно малой при хa, если .

БМ функции принято обозначать греческими буквами:(х), (х) и т.д, так и будем делать. Перевод определения на язык -:

(х) - БМ при хa  { : 0<| x-a |<|(х)|<}.

Если при х, lim f(х)=0 то f(x) бесконечно малая при х, если >0:()>0: х: 0<|х|>  |f(х)|<

Произведение БМ на ограниченную функцию - БМ функция.

Док-во. Пусть (х) - БМ при хa, f(x) ограничена в окрестности точки a. Требуется доказать, что (х) f(x) - БМ при хa. С>0: | f(x) |<C; 0 : 0<| x-a |<|(х)|</C

| (х) f(x)|<, т.е. (х) f(x) действительно БМ при хa.

Алгебраическая сумма конечного числа БМ функций - БМ функция.

Док-во. Пусть (х), (х) - БМ при хa. Требуется доказать, что (х) (х) - БМ при хa. 0 ₁: 0<| x-a |<₁|(х)|</2; ₂: 0<| x-a |<₂|(х)|</2. Если взять 0<| x-a |<min{₂,₁}=, то | (х) (х)| | (х) |+ | (х)| /2+/2=, т.е. (х) (х) действительно БМ при хa.

Следствие: Линейная комбинация БМ функций - БМ функция.

Вопрос 2

Главная часть приращения у дифференцируемой функции, линейная относительно приращения х аргумента (т.е. ), называется дифференциалом функции и обозначается dy (или df(x)).

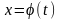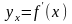6.8.2. Инвариантность формы первого дифференциала. Здесь мы рассмотрим одно важное свойство дифференциала, следующее из формулы для производной сложной функции (раздел 6.5.5. Производная сложной функции): если функции и имеют в соответствующих точках производные и , то производная сложной функции равна .

Если х - независимая переменная, то формула для дифференциала: . Если , то . Таким образом, независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же. Это свойство и называется инвариантностью формы первого дифференциала, и часто применяется в теории и решении задач. Ниже (раздел 6.10) мы с помощью этого свойства выведем формулу для производной функции, заданной параметрически.

6.8.3. Правила для вычисления дифференциала. Примеры вычисления дифференциала. Правила для вычисления дифференциала - прямое следствие правил дифференцирования (раздел 6.5):

1. ;

2. ;

3. ;

4. .

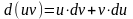Докажем, для примера, формулу 3: .

При нахождении дифференциала можно вычислить производную и затем применить формулу

вычисления дифференциала:

Дифференциалы высших порядков также определяются индуктивно: дифференциалом второго порядка (или вторым дифференциалом) функции называется дифференциал от её первого дифференциала; дифференциалом третьего порядка называется дифференциал от второго дифференциала; и вообще, дифференциалом n-го порядка функции называется дифференциал от её n-1-го дифференциала. При вычислении высших дифференциалов необходимо учитывать, что дифференциал независимой переменной - произвольная и независимая от х величина, которая при дифференцировании рассматривается как постоянная. Поэтому ; ; …., .

Билет №30