Вопрос 2

     Формула Тейлора

(R_n(x) - остаточный член формулы Тейлора

  Остаточный член формулы Тейлора    В форме Пеано:

при

Разложение

Разложение sin(x)

Формула Маклорена для функции sin x

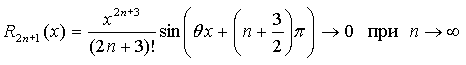
Билет №26

Вопрос 1

Если  - б. м. (при ) функция и 0 в некоторой окрестности точки а, то функция  есть б. б. функция при .

Если  - (при )  б. б. функция, то функция  есть б. м. функция при .

Билет №26

Вопрос 2

В математическом анализе правилом Лопита́ля называют метод нахождения пределов функций, раскрывающий неопределённости вида 0 / 0 и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Правило говорит, что если функции f(x) и g(x) обладают следующим набором условий:

1. или ;

2. ;

3. в проколотой окрестности a;

4. Если g(x) и f(x) — дифференцируемы в проколотой окрестности a,

тогда существует . При этом теорема верна и для других баз (для указанной будет приведено доказательство).

Билет №27

Вопрос 1

Коши Число b называется пределом функции в точке а ,если для любого числа >0 существует такое число  , что если для всех х не равном а удовлетворяющих неравенству |x-а| <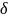 , выполняется неравенство|f(x) –b|< Обозначения: ;

Краткая форма записи: .

Геометрический смысл :

Неравенство расписывается в виде двустороннего неравенства как 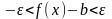или 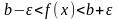. Аналогично неравенство можно расписать как . Поэтому смысл определения предела таков: , если для любой окрестности точки b найдётся такая -окрестности точки а что для всех х не равном а из этой - окрестности соответствующие значения функции лежат в окрестности точки b.

Теор. (о локальной ограниченности функции, имеющей предел). Если функция имеет предел b при ха, то она ограничена в некоторой окрестности точки а.

Док-во. Возьмём =1. : 0<| x-a |< | f(x)- b |<1 -1< f(x)- b<1 b-1< f(x)< b+1в -окрестности точки а f(x) ограничена сверху и снизу она в этой окрестности ограничена.

Теор. (о сохранении функцией знака предела). Если функция имеет предел b при ха, и число b>0 (либо b<0), то существует окрестность точки а, в которой f(x)>0 (либо f(x)<0).

Док-во. Рассмотрим для определённости случай b>0. Возьмём = b/2. : 0<| x-a |< | f(x)- b |< b/2 - b/2< f(x)- b< b/2 b- b/2< f(x)< b+ b/2 f(x)> b/2>0, что и требовалось доказать.

Очевидные следствия: 1. Если b>B, то f(x)> B в некоторой окрестности предельной точки; 2. Если f(x)>0 в некоторой окрестности предельной точки, то не может быть b<0.

Билет №27

Вопрос 2

График функции имеет на интервале выпуклость, направленную вниз, если он расположен не ниже любой касательной, проведённой на этом интервале.

График функции имеет на интервале выпуклость, направленную вверх, если он расположен не выше любой касательной, проведённой на этом интервале.

Теор.8.5.1. (Достаточное условие выпуклости графика функции). Если функция имеет на интервале вторую производную, и ( ) для , то её график имеет на этом интервале выпуклость, направленную вниз (вверх).

Док-во. Пусть, для определённости, на . Пусть с - произвольная точка , докажем, что график функции лежит выше касательной, проведённой к нему в точке 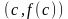. Уравнение касательной: ( - текущая точка касательной).

По формуле Тейлора . Вычитая из этого равенства предыдущее, получим на , т.е. точка графика функции действительно лежит выше точки графика касательной. Аналогично рассматривается случай на .