§ 2. Канонические и параметрические уравнения прямой в пространстве

 

Пусть в декартовой системе координат дан вектор a={p,q,r} и точка М₀=(x₀,y₀,z₀).

Построим прямую l, проходящую через т. М₀, параллельную вектору a (этот вектор называютнаправляющим вектором прямой).

Утверждение 2: М  l  М₀М || a.

М₀М={x-x₀, y-y₀, z-z₀} || a    t R, т.ч. М₀М=t·a => 

• Параметрические уравнения прямой в пространстве:

(**)

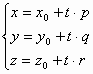Вы никогда не сталкивались с параметрическим заданием кривых? Поясним на примере: представьте себе, что по заранее намеченному маршруту с известной скоростью движется турист (автомобиль, самолёт, подводная лодка, как Вам больше понравится). Тогда, зная точку начала его путешествия, мы в любой момент времени знаем, где он находится. Таким образом, его положение на маршруте определяется всего одним параметром – временем.

В нашем случае турист движется по бесконечной прямой в пространстве, в момент времени t₀=0 он находится в точке М₀, в любой другой момент времени t его координаты в пространстве вычисляются по формулам (**).

Теперь несколько преобразуем формулы (**).

Выразим из каждой строчки параметр t: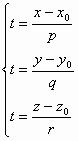 

• Канонические уравнения прямой в пространстве:

Замечание 2: Эта компактная запись на самом деле содержит три уравнения.

Замечание 3: Это формальная запись и выражение вида   в данном случае допустимо.

Замечание 4: Надо понимать, что для уравнения плоскости (прямой) играет роль именно направление перпендикулярного (направляющего) вектора, а не он сам. Т.о. вполне допустимо из каких-либо соображений заменять данный (или полученный в ходе решения) вектор на пропорциональный ему. Целесообразно также упрощать полученное уравнение, деля все его коэффициенты на общий множитель.

 

Пример 3. Написать канонические и параметрические уравнения прямой, параллельной заданной прямой и проходящей через заданную точку.

Пример 4. Написать канонические уравнения прямой, заданной пересечением двух плоскостей.

Пример 5. Найти точку пересечения прямой и плоскости.

 

§3. Расстояние от точки до плоскости в пространстве

 

Пусть в декартовых координатах плоскость Π задана уравнением: Ax+By+Cz+D=0, а точка М₁=(x₁,y₁,z₁).

Утверждение 3: расстояние от точки М₁ до плоскости Π вычисляется по формуле:

Пример 6. Найти расстояние от точки до плоскости.

 

§4. Координаты точки, делящей отрезок в заданном соотношении

 

Пусть в декартовой системе координат М₁=(x₁,y₁,z₁), М₂=(x₂,y₂,z₂) .

Утверждение 4: Координаты т. М, т.ч. М₁М=λ∙ММ₂, находятся по следующим формулам:

.

19) Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

     (10)

Это условие может быть записано также в виде

k₁k₂ = -1.     (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A₁A₂ + B₁B₂ = 0.     (12)

20)Условия параллельности и перпендикулярности прямой и плоскости

 

Пусть прямая задана каноническими уравнениями  , а плоскость общим уравнением  .

Прямая и плоскость параллельны тогда и только тогда, когда направляющий вектор прямой   и нормальный вектор плоскости   перпендикулярны, то есть их скалярное произведение равно нулю   – условие параллельности прямой и плоскости

Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой   и нормальный вектор   плоскости коллинеарны  – условие перпендикулярности прямой и плоскости.

Пример. Найти угол между прямой   и плоскостью  .

Решение. По условию  ,  , тогда  .

Из уравнения плоскости имеем, что нормальный вектор  . Следовательно  =  .

21) Угол между прямой и плоскостью

Дана плоскость   и точка А вне этой плоскости.

Проекцией точки А на плоскость   называется основание Q перпендикуляра, проведенного из этой точки к плоскости.

Пусть а — произвольная прямая, пересекающая плоскость   в точке О, причем прямая а не перпендикулярна плоскости   (рис. 40).

Прямая а и перпендикуляр AQ (А € а) определяют плоскость  ,   _|_  .

Прямая a1, проходящая через точки О и Q, называется проекцией а на плоскость  .

Углом между прямой а и плоскостью  , пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой а и ее проекцией a1 на плоскость   (рис. 40).

Если прямая а перпендикулярна плоскости  , то ее проекцией на плоскость представляет собой точку О, а угол между а и   считается прямым (равным 90°).

Если прямая а параллельна плоскости  , то угол между ними принимают равным нулю.

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями

Рассмотрим векторы   и  . Если угол между ними острый, то он будет  , где φ – угол между прямой и плоскостью. Тогда  .

Если угол между векторами   и   тупой, то он равен  . Следовательно  . Поэтому в любом случае  . Вспомнив формулу вычисления косинуса угла между векторами, получим  .

Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой   и нормальный вектор   плоскости коллинеарны, т.е.  .

Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы   и   перпендикулярны.

Примеры.

Написать уравнение плоскости, проходящей через точку М1(2;-3;4) параллельно прямым   и  .

Так как M1 α, то уравнение плоскости будем искать в виде

.

Применяя условие параллельности прямой и плоскости, получим систему линейных уравнений 

Отсюда

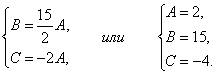
Итак,   или  .

22)

Определение окружности, данное в раньше, легко переводится на координатный язык. Пусть точка Q -- центр окружности (привычной буквой O мы обозначили начало координат) имеет координаты (a; b), R - радиус окружности, M(x; y) - некоторая точка на окружности. По определению окружности QM = R. Теперь остается выразить MQ по известной формуле через координаты точек M и Q и возвести равенство в квадрат. В результате имеем    Получившееся уравнение и является уравнением окружности с центром в точке Q(a; b) и радиусом R. К оординаты любой точки M(x; y) окружности удовлетворят тому уравнению, а любая точка M(x; y), координаты которой удовлетворят тому уравнению, лежит на окружности.

При решении геометрических задач координатным методом в большинстве случаев не ограничиваются первым этапом - переводом на алгебраический язык и решением алгебраической задачи. Мы должны также суметь дать геометрическое толкование полученному алгебраическому результату, в частности, увидеть в получившемся соотношении уравнение окружности и в том случае, когда это уравнение записано в нестандартном виде.

Следует запомнить, что уравнение

x² + y² + ax + by + c = 0

задает либо окружность, либо точку, либо пустое множество. Чтобы ответить на вопрос, какой именно случай имеет место для данного конкретного уравнения, надо выделить полные квадраты по x и y. С этим приемом вы уже встречались на уроках алгебры при изучении квадратного трехчлена. например, уравнение x² + y² - 4x + 2y = 0 можно преобразовать так:

(x² - 4x + 4) + ( y² + 2y + 1) - 5 = 0, (x - 2)² + (y + 1)² = 5.

Таким образом, рассматриваемое уравнение задает окружность с центром в точке Q(2; -1) и радиусом  .

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Основные термины

Касательная

П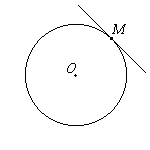 рямая, имеющая с только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойства касательной

1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

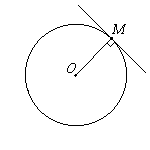
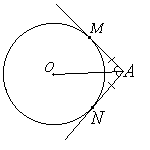
2. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Хорда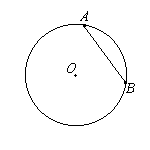

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

2. Дуги, заключенные между параллельными хордами, равны.

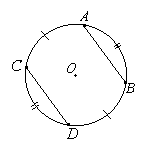
3. Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Свойства окружности

1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).

2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

3. Точка касания двух окружностей лежит на линии, соединяющей их центры.

Теорема о касательной и секущей

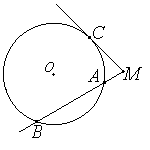
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC² = MA•MB.

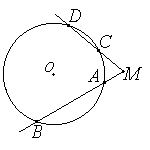
Теорема о секущих

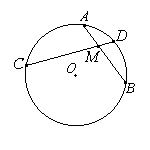
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

У глы в окружности

Центральным углом в окружности называется плоский угол с вершиной в ее центре.

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Любые д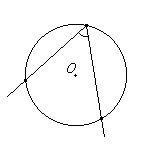 ве точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.

Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.