1) Двухмерная система координат

Декартовыми прямоугольными координатами точки P на плоскости в двухмерной системе координат называются взятые с определенным знаком расстояния (выраженные в единицах масштаба) этой точки до двух взаимно перпендикулярных прямых — осей координат или проекции радиус-вектора rточки P на две взаимно перпендикулярные координатные оси.

В двухмерной системе координат горизонтальная ось называется осью абсцисс (ось OX), вертикальная ось — осью ординат (ось ОY). Положительные направления выбирают на оси OX — вправо, на оси OY — вверх. Координаты x иy называются соответственно абсциссой и ординатой точки. Запись P(a,b) означает, что точка P на плоскости имеет абсциссу a и ординату b.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

Связь между декартовыми и полярными координатами

Пару полярных координат r и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:

x = rcos φ,

y = rsin φ,

в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:

r² = y² + x² (по теореме Пифагора).

Для определения угловой координаты следует принять во внимание два следующие соображения:

• Для , может быть произвольным действительным числом.

• Для 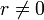, чтобы получить уникальное значение , следует ограничиться интервалом в 2π. Обычно выбирают интервал или .

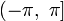Д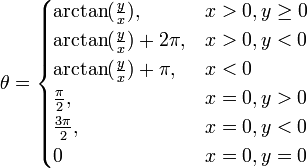 ля вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):

Д ля вычисления в интервале , можно воспользоваться такими уравнениями:^[14]

Учитывая, что для вычисления полярного угла не достаточно знать отношение y к x, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты x.

Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенныечерез начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O , положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектора) (см. рис. 1). Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.

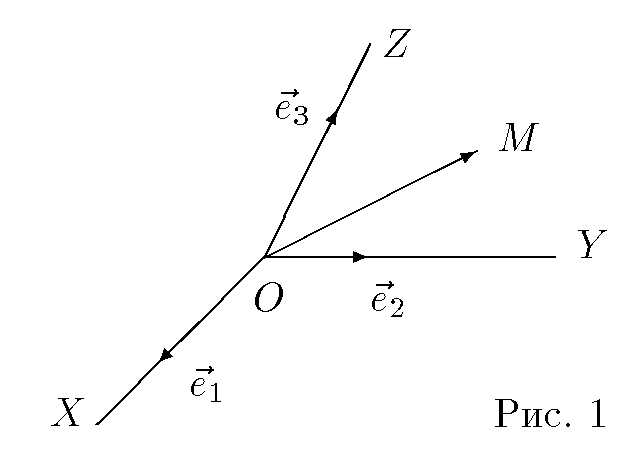
Поверхностью 2–го порядка называется поверхность, которая в некоторой прямоугольной декартовой системе координат определяется уравнением

Ax2 + By2 + Cz2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Kz + L = 0

где A² + B² + C² ≠ 0 .

Цилиндрические и сферические координаты определяются точкой O , исходящим из нее лучом  и единичным вектором 

→

n

, перпендикулярным  (рис. 2).

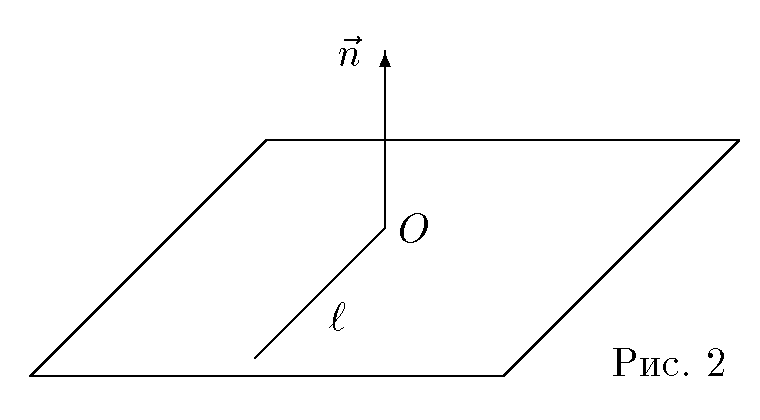
Проведем через точку O перпендикулярно вектору 

→

n

 плоскость P и обозначим проекцию точки M на эту плоскость M' .

В цилиндрических координатах положение точки M определяется числами ρ ,  и z , где ρ и  — полярные координаты точки M' , а z — проекция вектора OM на вектор

→

n

 .

Пусть точка O совпадает с началом прямоугольной декартовой системы координат, луч  — с положительной частью оси абсцисс, а вектор 

→

n

 — с положительной частью оси аппликат (рис. 3).

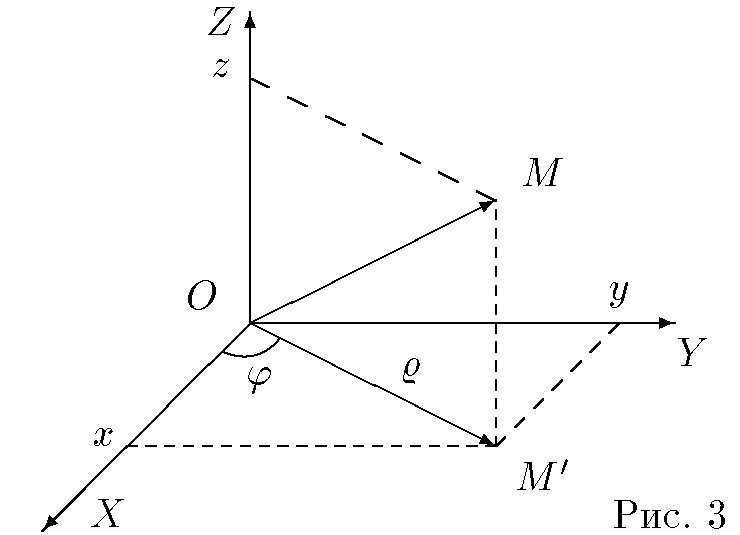
Декартовы координаты x , y и z точки M выражаются через ее цилиндрические координаты ρ ,  и z по формулам

x = ρcos,  y = ρsin,  z = z.

В сферических координатах положениеточки M определяется числами ρ ,  и θ , где ρ = |OM| ,  — полярный угол точки M' , а θ — угол между векторами 

→

n

и OM .Мы будем отсчитывать угол θ от вектора 

→

n

 по направлению к вектору OM . Угол θ принимает значения от 0 до π .

Пусть точка O совпадает с началом прямоугольной декартовой системы координат, луч  — с положительной частью оси абсцисс, а вектор 

→

n

 — с положительной частью оси аппликат (рис. 4), то

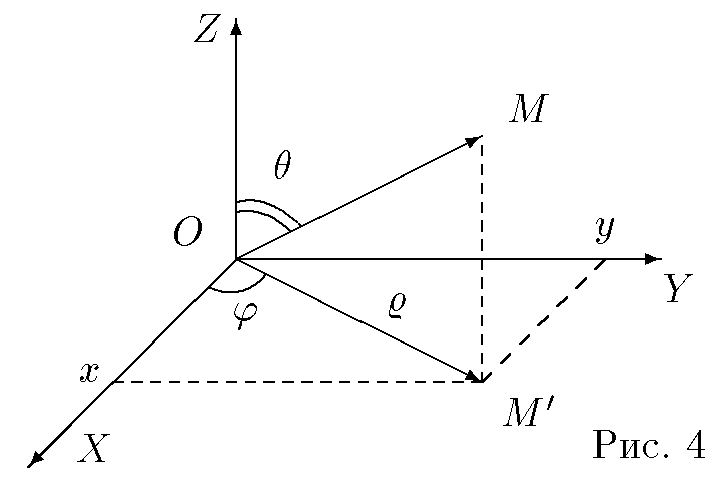
Декартовы координаты x , y и z точки M выражаются через ее сферические координаты ρ ,  и θ по формулам

x = ρcossinθ,  y = ρsinsinθ,  z = ρcosθ

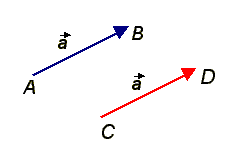
2) Геометрические векторы: основные понятия

Геометрическим вектором называется направленный отрезок, который можно перемещать параллельно ему самому.

Направленный отрезок с началом в точке A и концом в точке B обозначается AB. Векторы обозначаются строчными латинскими буквами со стрелками: 

→

a

, 

→

r

, 

→

x

, ….

Таким образом, два направленных отрезка AB и CD, имеющие одинаковые длины и направления, изображают один и тот же вектор 

→

a

, и именно в этом смысле мы будем писать равенства между векторами и направленными отрезками, например:

→ a  = AB = CD

Всегда выражение "вектор AB" означает вектор, изображаемый направленным отрезком AB.

Длиной (или модулем) вектора AB называется расстояние между точками A и B. Будем считать, что единица измерения длин выбрана и, говоря о длинах отрезков, не будем указывать, какой единицей они измеряются. Модуль вектора AB обозначается символом |AB|. Вектор нулевой длины называется нулевым и обозначается символом 

→

0

Вектор BA, равный по длине вектору AB и противоположно направленный, называется противоположным и обозначается −AB. Вектор, длина которого равна 1, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора AB, называется ортом вектора AB и обозначается AB_e.

Углом между векторами 

→

a

 и 

→

b

 называется угол α (0 ≤ α ≤ π), образованный этими векторами, при условии, что начальные точки этих векторов совпадают (этого можно добиться параллельным переносом векторов).Векторы, лежащие на праллельных или совпадающих прямых, называются коллинеарными.

Векторы, лежащие в праллельных или совпадающих плоскостях, называются компланарными. Если угол между векторами равенπ/2, то векторы называются ортогональными.

3) Сложение векторов

Параллельный перенос

Под параллельным переносом вдоль вектора понимают перемещение всех точек пространства в одном направлении на одинаковое расстояние. Определим сложение векторов так, чтобы последовательные сдвиги вдоль двух векторов соответствовали сдвигу вдоль суммы этих векторов.

Пусть даны два вектора   и  . Приложим вектор   к некоторой точке O, получим  . Приложим вектор   к точке A, получим  . Тогда вектор   будем называть суммой векторов:  .

Докажем, что данное определение не зависит от выбора точки O.

Приложим вектор   к другой точке O', получим  . Приложим вектор   к точке A', получим  .

Рассмотрим направленные отрезки   и  . Они, очевидно, равны (см. рис.), поскольку OBB'O' — параллелограмм.