
- •2) Геометрические векторы: основные понятия
- •3) Сложение векторов
- •Умножение на число
- •Свойства линейных операци
- •6) Линейные операции над векторами в координатной форме
- •Действия с векторами в координатной форме
- •Как найти угол между двумя векторами
- •Инструкция
- •14) Уравнение пучка прямых
- •§ 2. Канонические и параметрические уравнения прямой в пространстве
- •§3. Расстояние от точки до плоскости в пространстве
- •§4. Координаты точки, делящей отрезок в заданном соотношении
- •Свойства углов, связанных с окружностью
- •Длины и площади
- •Вписанные и описанные окружности о кружность и треугольник
- •Окружность и четырехугольники
- •23) Каноническое уравнение эллипса
- •25) Парабола
- •Виды матриц
- •Матрицы специального вида
- •2. Существует такое натуральное число r, удовлетворяющее неравенствам , что .
- •3. Если какой-либо диагональный элемент , то все элементы I-й строки и всех последующих строк равны нулю.
- •30) Обратная матрица
- •32) Система линейных уравнений, ее решение, различные формы записи системы линейных уравнений, определение однородной,неоднородной,совместной,несовместной,определенной и неопределенной систем.
- •Векторная форма записи
- •Матричная форма записи
- •33) Решение систем линейных уравнений
- •34) Описание метода
- •3 7)Решение систем линейных уравнений методом Гаусса
- •[Править]Условие совместности
- •Алгоритм Описание
- •39) Однородные системы линейных уравнений.
- •42) Линейно зависимые и линейно независимые системы векторов векторного пространства
- •43) Размерность и базис линейного пространства, координаты вектора
- •Линейная оболочка системы векторов. Подпространство. Базис подпространства
- •Определения
- •Изоморфизм
- •46) Собственные числа и собственные векторы
- •Основная терминология
- •Геометрическая модель
- •Действия над комплексными числами
- •50) Тригонометрическая и показательная формы
- •Определение
- •Связанные определения
- •Свойства
34) Описание метода
Для системы n линейных уравнений с n неизвестными (над произвольным полем)

с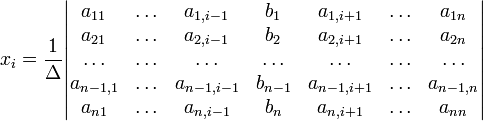 определителем матрицы системы Δ,
отличным от нуля, решение записывается
в виде
определителем матрицы системы Δ,
отличным от нуля, решение записывается
в виде
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы дляопределителя Грама и Леммы Накаямы.
35) Теорема Кронекера-Капелли |
Для
того чтобы система m неоднородных
линейных уравнений с n неизвестными
была совместной, необходимо и
достаточно, чтобы Доказательство необходимости. Пусть система (1.13) совместна, то есть существуют такие числа х1=α1, х2=α2, …, хn=αn, что
Вычтем
из последнего столбца расширенной
матрицы
ранг
которой в результате элементарных
преобразований не изменится и Доказательство достаточности.
Пусть
Это означает, что остальные строки матрицы могут быть получены как линейные комбинации первых r строк, то есть m-r строк матрицы можно представить в виде сумм первых r строк, умноженных на некоторые числа. Но тогда первые r уравнений системы (1.13) самостоятельны, а остальные являются их следствиями, то есть решение системы первых r уравнений автоматически является решением остальных уравнений. Возможны два случая. 1. r=n. Тогда система, состоящая из первых r уравнений, имеет одинаковое число уравнений и неизвестных и совместна, причем решение ее единственно. 2. r<n. Возьмем первые r уравнений системы и оставим в левых частях этих уравнений первые r неизвестных, а остальные – перенесем вправо:
«Свободным» неизвестным xr+1, xr+2, …, xn можно придать какие угодно значения. Тогда соответствующие значения получают неизвестные x1, x2, …, xr. Система (1.13) и в этом случае совместная, но неопределенная. Замечание. Отличный от нуля минор порядка r, где r<n, будем называть базисным минором. Неизвестные х1, х2, …, хr так же называют базисными, остальные – свободными. Систему (1.16) называют укороченной. Если свободные неизвестные обозначить хr+1=c1, хr+2=c2, …, хn=cn-r, то базисные неизвестные будут от них зависеть, то есть решение системы m уравнений с n неизвестными будет иметь вид X = (x1(c1, …, cn-r), x2(c1, …, cn-r), …, xr(c1, …, cn-r), c1, c2, …, cn-r)T, где значок Т означает транспонирование. Такое решение системы называется общим. |
36)ус-е определенности, неопределенности Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
|
Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].
Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой

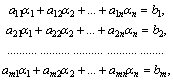 (1.15)
(1.15)

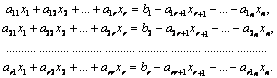 (1.16)
(1.16)