30) Обратная матрица
Определение
14 . 8 Матрица 
называется
обратной матрицей для квадратной
матрицы 
,
если 
.
Из определения
следует, что обратная матрица
будет
квадратной матрицей того же порядка,
что и матрица
(иначе
одно из произведений 
или 
было
бы не определено). Обратная матрица для
матрицы
обозначается 
.
Таким образом, если
существует,
то 
.
Из определения обратной матрицы следует,
что матрица
является
обратной для матрицы
,
то есть 
.
Про матрицы
и
можно
говорить, что они обратны друг другу
или взаимно обратны. Предложение
14 . 20 Если матрица
имеет
обратную, то 
и
.
Доказательство
. Так как определитель
произведения матриц равен произведению
определителей ( предложение 14.7 ),
то
.
По следствию 14.1 
,
поэтому 
,
что невозможно при 
.
Из предыдущего равенства следует
также
.
Последнее предложение
можно сформулировать в следующем виде.
Если определитель матрицы равен нулю,
то обратная к ней не существует. Так
как для нахождения обратной матрицы
важно, равен ли определитель марицы
нулю или нет, то введем следующие
определения. Определение
14 . 9 Квадратную матрицу
назовем
вырожденной или особенной матрицей ,
если
,
и невырожденной или неособенной матрицей
, если
.
Предложение
14 . 21 Если обратная матрица существует,
то она единственна.
Доказательство . Пусть
две матрицы
и 
являются
обратными для матрицы
.
Тогда 
и
Следовательно, 
.
Предложение
14 . 22 Если квадратная матрица
является
невырожденной, то обратная для нее
существует и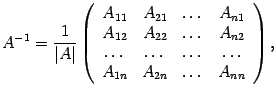
(
14 .14) где 
--
алгебраические дополнения к элементам 
.
Доказательство
. Так как для невырожденной
матрицы
правая
часть равенства ( 14.14 ) всегда
существует, то достаточно показать,
что эта правая часть является о
братной
матрицей для матрицы
.
Обозначим правую часть равенства (
1
4.14
) буквой
.
Тогда нужно п
роверить,
что
и
что 
.
Докажем первое из этих равенств, второе
доказывается аналогично. Пусть 
.
Найдем элементы матрицы
,
учитывая, что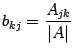
: 
Если 
,
то по предложению 14.17 сумма справа
равна нулю, то есть 
при
.
Если
,
то 
Сумма
справа представляет собой разложение
определителя матрицы
по 
-ой
строке ( предложение 14.16 ). Таким
образом,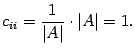
Итак,
в матрице
диагональные
элементы равны 1, а остальные равны
нулю, то есть 
.
Результаты предложений
14.20 , 14.21 , 14.22 соберем в одну теорему.
Теорема 14 .
1 Обратная матрица для квадратной
матрицы
существует
тогда и только тогда, когда матрица
--
невырожденная, обратная матрица
единственна, и справедлива формула (
14.14 ). Замечание
14 . 12 Следует обратить особое внимание
на места, занимаемые алгебраическими
дополнениями в формуле обратной матрицы:
первый индекс показывает номер столбца
, а второй -- номер строки , в которые
нужно записать вычисленное алгебраическое
дополнение.
Пример 14 . 7
Найдите обратную матрицу для
матрицы 
.
Решение. Находим определитель
Так
как
,
то матрица
--
невырожденная, и обратная для нее
существует. Находим алгебраические
дополнения:
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй -- строке: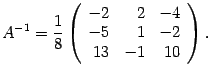 
(
14 .15) Полученная матрица и служит ответом
к задаче.
Замечание
14 . 13 В предыдущем примере было бы
точнее ответ записать так: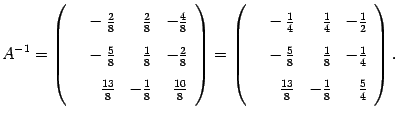
(
14 .16) Однако запись ( 14.15 ) более
компактна и с ней удобнее проводить
дальнейшие вычисления, если таковые
потребуются. Поэтому запись ответа в
виде ( 14.15 ) предпочтительнее, если
элементы матриц -- целые числа. И
наоборот, если элементы матрицы
--
десятичные дроби, то обратную матрицу
лучше записать без множителя 
впереди.
Замечание
14 . 14 При нахождении обратной матрицы
приходится выполнять довольно много
вычислений и необычно правило расстановки
алгебраических дополнений в итоговой
матрице. Поэтому велика вероятность
ошибки. Чтобы избежать ошибок следует
делать проверку: вычислить произведение
исходной матрицы на итоговую в том или
ином порядке. Если в результате получится
единичная матрица, то обратная матрица
найдена правильно. В противном случае
нужно искать ошибку.
Пример 14 . 8
Найдите обратную матрицу для
матрицы 
.
Решение. 
--
существует. 
Ответ: 
.
Нахождение
обратной матрицы по формуле ( 14.14 )
требует слишком много вычислений. Для
матриц четвертого порядка и выше это
неприемлемо. Реальный алгоритм нахождения
обратной матрицы будет приведен позже.
Теорема существования и единственности решения задачи Коши
У
кажем
достаточные условия существования и
единственности решения задачи Коши
.
(1)
Теорема Пикара. Пусть функция непрерывна в прямоугольнике
и
удовлетворяет условию Липшица
по y равномерно
относительно x,
т.е. 
,
для всех x, 
и 
.
Пусть
,
тогда
задача Коши (1) на промежутке 
имеет
единственное решение 
.
Замечание. Условие
Липшица в теореме Пикара можно заменить
на требование ограниченности или
непрерывности 
в
каждом компакте из области определения
дифференциального уравнения.
Решение
задачи Коши при выполнении условий
теоремы Пикара можно найти как предел
при 
равномерно
сходящейся последовательности функций 
,
определяемых рекуррентным соотношением
. (2)
Оценка
погрешности, получаемой при замене
точного решения y(x) n- м
приближением 
,
выражается неравенством
.
Теорема
Пеано. Пусть
функция непрерывна
в прямоугольнике 
,
причем
.
Тогда задача Коши на промежутке имеет по крайне мере одно решение .
Система уравнений
в векторных обозначениях записывается в виде
,
(3)
где 
и 
-
векторы. Непрерывность вектор -
функции f означает
непрерывность всех функций 
,
а вместо 
рассматривается
матрица из частных производных 
.
Рассмотренные
выше теоремы остаются справедливы и
для системы, записанной в виде (3). При
этом |y| означает
длину вектора y: 
.
Рассмотрим уравнение вида
.
(4)
Пусть
в области D функция f и
ее частные производные первого порядка
по 
непрерывны,
и точка 
лежит
внутри D.
Тогда при начальных условиях
уравнение (4) имеет единственное решение.
Уравнение
(4) можно свести к системе вида (2), если
ввести новые неизвестные функции по
формулам 
.
Тогда уравнение (4) сводится к системе
,
которая является частным случаем системы (3) и к которой применимы все рассмотренные утверждения.
Часто решение задачи Коши существует не только на отрезке, указанном в теоремах, но и на большем отрезке.
Если
функция f(x,y) удовлетворяет
в прямоугольнике
условиям
теоремы Пикара, то всякое ее решение 
можно
продолжить до выхода на границу
прямоугольника
. Если
функция f(x,y) в
полосе 
непрерывна
и удовлетворяет неравенству 
,
где a(x) и b(x) -
непрерывные функции, то всякое решение
уравнения (1) и (3) можно продолжить на
весь интервал 
.
Пример
1. Построить
последовательные приближения 
к
решению данного уравнения с данными
начальными условиями: 
.
Решение.
Последовательные приближения к решению данной задачи определим по рекуррентной формуле
.
Подставляя в последнюю формулу поочередно n=0,1 найдем нужные приближения:
,
.
Пример
2. Указать
какой-нибудь отрезок, на котором
существует решение с данными начальными
условиями: 
.
Решение.
Воспользуемся
теоремой Пикара. В данном случае 
.
Функция f непрерывна
в любом прямоугольнике 
и
удовлетворяет условию Липшица, поскольку
производная 
ограничена
числом 
.
Следовательно, на сегменте 
,
где
существует единственное решение данной задачи. Найдем число
.
Ясно, что если на каком - то сегменте I существует единственное решение, то оно существует и на меньшем сегменте, вложенном в I. Отсюда следует, что желательно найти как можно больший отрезок I, т.е.
.
Так
как функция 
возрастает
при 
,
а функция 
убывает,
то
достигается
при условии, что 
,
т.е.
.
(5)
Взяв
производную по b от
правой части (5), найдем, что при 
достигается
максимум a,
который легко вычислить, подставив
значение 
в
(5). Тогда получим
.
Таким
образом, можно гарантировать существование
и единственность решения данной задачи
на сегменте 
.
Пример 3. При
каких начальных условиях существует
единственное решение уравнения 
.
Решение.
Поскольку функция
вместе с частными производными
непрерывна
при 
и 
,
то через каждую точку 
,
где 
и 
,
проходит единственная интегральная
кривая уравнения
.
Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы.
Вычисление обратной матрицы
Пусть A=(aij) – квадратная матрица с определителем, не равным нулю. Тогда существует обратная матрица A–1, которая вычисляется по формуле
.
Последняя формула означает, что в i-й строке и j-м столбце обратной матрицы располагается алгебраическое дополнение элемента, стоящего в j-й строке и в i-м столбце исходной матрицы, деленное на определитель исходной матрицы.
Напомним здесь, что Apq=(–1)p+qMpq, где Mpq называется минором и представляет собой определитель, получающийся из определителя detA вычеркиванием p-й строки и q-го столбца.
Рассмотрим пример:
detA=20+6–24=2;
.
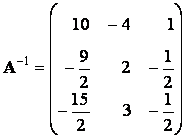Еще раз подчеркнем, что обратная матрица существует только для квадратной матрицы с определителем, отличным от нуля!
Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.
31) Рангом системы строк (столбцов) матрицы A с m строк и nстолбцов называется максимальное число линейно независимыхстрок (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.
Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.
Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.
Обычно
ранг матрицы A обозначается 
(
)
или 
.
Оба обозначения пришли к нам из
иностранных языков, потому и употребляться
могут оба. Последний вариант свойственен
для английского языка,
в то время как первый —
длянемецкого, французского и
ряда других языков.
Определение. В матрице порядка mxn минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n. Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.
В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.
Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А. Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными. Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.
Определение. Матрица 
,
полученная из матрицы 
при
помощи элементарных преобразований,
называется эквивалентной и
обозначается А 
В.
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица называется ступенчатой если она имеет вид:
,
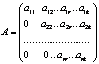где 
, 
, 
.
Очевидно,
что ранг ступенчатой матрицы равен
числу ненулевых строк 
,
т.к. имеется минор
-го
порядка, не равный нулю:
.
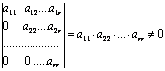Пример. Определить ранг матрицы с помощью элементарных преобразований.
.
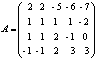
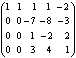
Ранг
матрицы равен количеству ненулевых
строк, т.е. 
.