17.Економічна та математична постановка задачі про призначення.

(1., стр.250).

Задача про призначення. Потрібно виконати n видів робіт, на які претендують n кандидатів. Витрати на оплату праці i-го кандидата за виконання j-ої роботи дорівнюють . Кожен кандидат може бути призначений лише на одну роботу, і кожна робота має виконуватися лише одним кандидатом. Потрібно знайти оптимальне призначення кандидатів на виконання робіт, за якого сумарні витрати на виконання всіх робіт будуть мінімальними.

Нехай дорівнює одиниці, якщо i-ий кандидат виконує j-ту роботу, та дорівнює нулю в протилежному разі. Тоді умову, що кожен кандидат має виконувати лише одну роботу, запишемо у вигляді: . Умова виконання кожної роботи лише одним канди­датом має вигляд: . Цільова функція має такий вираз: . Отже, маємо математичну модель транспортної задачі:

min

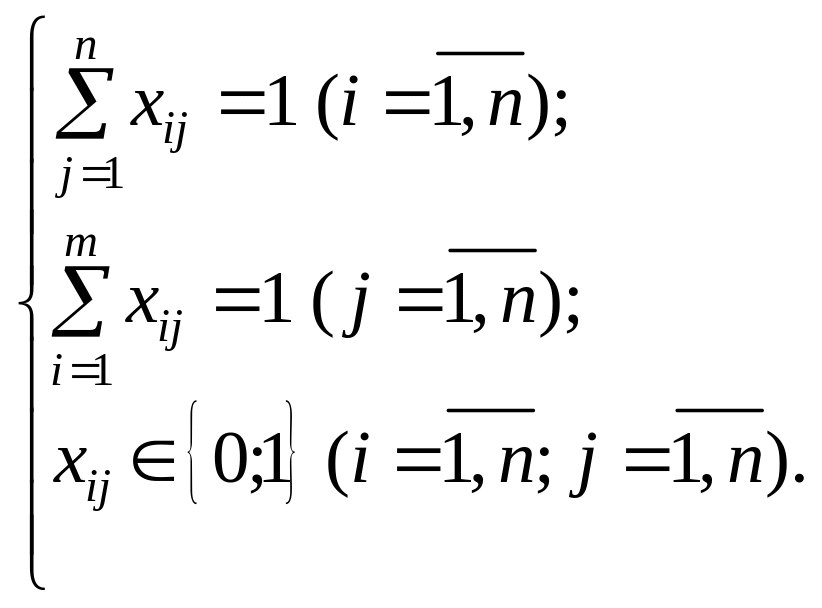
Найзручнішим методом розв’язання задачі про призначення є угорський метод.

18.Двохетапна транспортна задача.

(1., стр.230-231).

У класичній постановці транспортної задачі допускається, що вантаж перевозиться безпосередньо від постачальників до споживачів. Але на практиці досить часто зустрічається випадок, коли певна частина продукції спочатку перевозиться до посередницьких фірм (сховищ), а потім споживачам. У такому разі розв’язання задачі поділяють на два етапи: спочатку знаходять оптимальний план перевезень від постачальників до посередників, а потім — від посередників до споживачів. Така задача має назву двохетапної транспортної задачі.

Нехай в m пунктах постачання А₁, А₂, …, А_m є відповідно одиниць продукції, яку необхідно перевезти до l посередницьких фірм , місткості сховищ яких становлять , а потім доставити її споживачам , потреби яких становлять . Відомі також витрати на перевезення одиниці продукції від кожного постачальника до посередницьких фірм — та від посередників до споживачів — . Потрібно визначити оптимальну схему перевезень продукції з мінімальними сумарними витратами. Якщо обсяг продукції, що перевозиться від i-го постачальника до k-ої фірми, позначити через , а обсяг вантажу, що перевозиться від k-ої фірми j-му споживачеві — через , то математична модель задачі матиме вигляд:

за умов:

;

;

;

;

.

Зазначимо, що коли загальний обсяг вантажу дорівнює місткості всіх складів і баз , а також сумарній потребі всіх споживачів , тобто = = , то така двохетапна транспортна задача може бути розв’язана як дві одноетапні. В іншому разі окремі оптимальні плани двох задач не збігатимуться з оптимальним планом загальної задачі.

19.Економічна та математична постановка цілочислової задачі лінійного програмування.

(1., стр.255-256).

Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування. У тому разі, коли цілочислових значень мають набувати не всі, а одна чи кілька змінних, задача називається частково цілочисловою.

До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).

Умова цілочисловості є по суті нелінійною і може зустрічатися в задачах, що містять як лінійні, так і нелінійні функції. У даному розділі розглянемо задачі математичного програмування, в яких крім умови цілочисловості всі обмеження та цільова функція є лінійними, що мають назву цілочислових задач лінійного програмування.

Загальна цілочислова задача лінійного програмування записується так:

(6.1)

за умов:

; (6.2)

; (6.3)

— цілі числа . (6.4)

Слід зазначити, що у розглянутих в попередньому розділі класичній транспортній задачі та інших задачах транспортного типу (в задачах про призначення, про найкоротший шлях тощо) з цілочисловими параметрами початкових умов забезпечується цілочисловий розв’язок без застосування спеціальних методів, однак у загальному випадку вимога цілочисловості змінних значно ускладнює розв’язування задач математичного програмування.