2. Знаходження оптимальних планів прямої та двоїстої задачі на основі теорем двоїстості.

(2., стор.78-82).

До наведеної далі задачі лінійного програмування записати двоїсту задачу. Розв’язавши двоїс- ту задачу графічно, визначити оптимальний план прямої за- дачі.

Z = x₁ + 2x₂ + 2x₃  min;

Розв’язування. За відповідними правилами побудуємо двоїсту задачу:

F = y₁ + 4y  mах;

Зауважимо, що задачі несиметричні, і тому змінна у₁, що відповідає рівнянню в системі обмежень прямої задачі, може мати будь-який знак, а змінна у₂ — лише невід’ємна.

Двоїста задача має дві змінні, а отже, її можна розв’язати графічно (рис. 3.1).

Рис. 3.1

Найбільшого значення цільова функція двоїстої задачі F досягає в точці В многокутника ABCD. Її координати:

тобто Y ^* = (–2/3; 4/3); mах F = 1  (–2/3) + 4  4/3 = 14/3.

Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.

Підставимо Y ^* у систему обмежень двоїстої задачі і з’ясуємо, як виконуються обмеження цієї задачі:

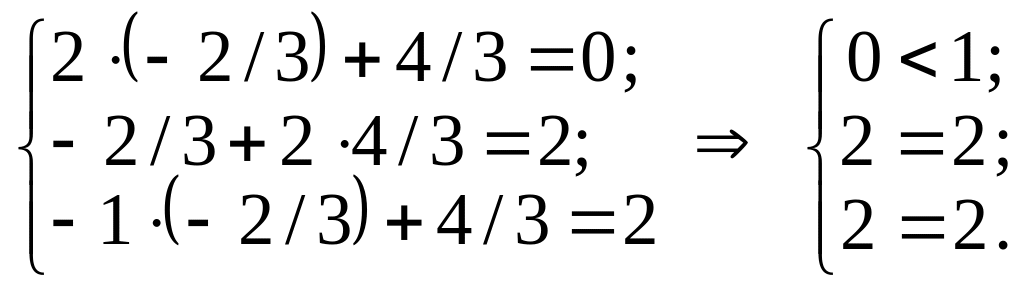
Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, доходимо висновку, що перша змінна прямої задачі дорівнюватиме нулю х₁ = 0 (перша частина другої теореми двоїстості).

Тепер проаналізуємо оптимальний план двоїстої задачі. Ос­кільки друга компонента плану у₂ = 4/3 додатна, доходимо висновку, що друге обмеження прямої задачі для X ^* виконуватиметься як строге рівняння (друга частина другої теореми двоїстості).

Об’єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х₁ = 0, та визначити решту змінних:

тобто X ^* = (0; 5/3; 2/3), min Z = 1  0 + 2  5/3 + 2  2/3 = 14/3.

Умова min Z = max F = 14/3 виконується, і тому X ^* = (0; 5/3; 2/3); Y ^* = (–2/3; 4/3) є оптимальними планами відповідно прямої та двоїстої задач.

Задача 3.3.

Визначити, чи оптимальні такі плани сформульова­ної задачі лінійного програмування:

Z = 12x₁ – 4x₂ + 2x₃  min;

а) х = (8/7; 3/7; 0); б) х = (0; 1/5; 8/5); в) х = (1/3; 0; 1/3).

Розв’язування. Принцип розв’язування задач такого типу ґрунтується на використанні другої теореми двоїстості. Необхідно побудувати двоїсту задачу та припускаючи, що відповідний план Х є оптимальним, визначити оптимальний розв’язок двоїстої задачі. Якщо при цьому екстремальні значення цільових функцій збігатимуться, то припущення правильне. Протилежного висновку можна дійти в таких випадках.

1. Якщо запропонований план Х недопустимий, тобто не задовольняє систему обмежень прямої задачі.

2. Якщо визначений план двоїстої задачі недопустимий, тобто не задовольняє всі обмеження двоїстої задачі.

3. Якщо визначений план двоїстої задачі допустимий, але для нього екстремальне значення цільової функції F не дорівнює зна­ченню функції Z, тобто не виконується умова першої теореми дво­їстості.

Запишемо двоїсту задачу до прямої задачі лінійного програмування:

F = y₁ + 2y₂  max;

Перевіримо запропоновані плани на оптимальність.

1. X = (8/7; 3/7; 0). Підставимо його в систему обмежень прямої задачі:

Обидва обмеження виконуються і тому Х = (8/7; 3/7; 0) є допустимим планом прямої задачі. Припустимо тепер, що зазначений план є оптимальним планом прямої задачі. Тоді для нього Z = 12  8/7 + 4  3/7 + 2  0 = 12.

Скористаємося другою теоремою двоїстості та визначимо відповідний план двоїстої задачі. Оскільки x₁ = 8/7 > 0; x₂ = 3/7 > 0, то згідно з другою частиною другої теореми двоїстості можна записати перше та друге обмеження як рівняння і визначити у₁ і у₂:

Підставимо ці значення в третє обмеження системи двоїстої задачі:

;

.

Для визначених значень у₁ = 4; у₂ = 4 це обмеження не виконується, і тому відповідний план Y = (4; 4) є недопустимим планом двоїстої задачі. Унаслідок цього наше припущення, що Х = (8/7; 3/7; 0) є оптимальним планом вихідної задачі, виявилося помилковим.

2. Х = (0; 1/5; 8/5). Підставимо цей план в систему обмежень прямої задачі:

План допустимий і для нього Z = 12  0 – 4  1/5 + 2  8/5 = 12/5.

Визначимо відповідний план двоїстої задачі. Оскільки компоненти x₃ та x₂ додатні, то друге та третє обмеження двоїстої задачі можна записати як рівняння:

Перевіримо, що виконується перше обмеження двоїстої задачі для визначених значень у₁ та у₂: 2  8/5 + 2/5 = 18/5 < 12. Отже, перше обмеження виконується, і тому Y = (8/5; 2/5) є допустимим планом двоїстої задачі. Для нього F = 8/5 + 2  2/5 = 12/5 = Z. З огляду на викладене можна зробити висновок, що Y ^* = (8/5; 2/5) є оптимальним планом двоїстої задачі, а X ^* = (0; 1/5; 8/5) — оптимальним планом прямої задачі.

Наше припущення відносно запропонованого плану виявилося правильним.

3. Х = (1/3; 0; 1/3). Для цього плану обмеження прямої задачі виконуються так:

Оскільки Х = (1/3; 0; 1/3) є недопустимим планом, то він не може бути також оптимальним планом прямої задачі.

Отже, перевірка запропонованих планів на оптимальність дала такі результати: а) ні; б) так, Y ^* = (0; 1/5; 8/5), min Z = 12/5; в) ні.