16. Доверительный интервал для параметра σ2 регрессионной модели.

Наряду с интервальными оценками функции регрессии иногда представляет интерес построения доверительных интервалов для параметров регрессионной модели , в частности для α, β и (дисперсии возмущения ε_i или зависимой переменной y_i).

При построении доверительного интервала для параметра исходят из того, что статистика имеет -распределение с k = n – 2 степенями свободы. Поэтому интервальная оценка для на уровне значимости α имеет вид:

(2.26)

Доверительный интервал выбирается таким образом, чтобы вероятность

17. Основная идея дисперсионного анализа

Для того чтобы проверить значимость уравнения регрессии необходимо установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

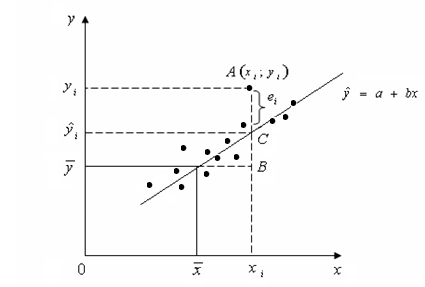Рисунок 2.4

На рисунке 2.3 изображены наблюдаемые значения переменных x_i , y_i, соответствующая этим значениям линия регрессии, обозначены составляющие регрессии:

По рисунку AB = CB + AC или

где – ордината точки прямой, соответствующей уравнении регрессии, имеющей абсциссу x_i.

Возведя обе части в квадрат и просуммировав выражение для каждого i-го случая, имеем

(2.28)

где - полная сумма квадратов;

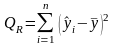- сумма квадратов, объясненная моделью;

- остаточная сумма квадратов.

Если поделить выражение на n , то получим

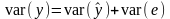, (2.29)

то есть дисперсия переменной у частично объясняется изменчивостью , а частично изменчивостью остатка регрессии.

Оценка этой изменчивости

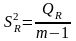(2.30)

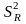– обусловлена уравнением регрессии или объясняющей переменной,

(2.31)

– воздействием неучтенных случайных факторов и ошибок.

18. Процедура проверки значимости линейной связи между переменными, использование f-критерия (критерия Фишера-Снедекора)

Эта процедура будет иметь смысл при соблюдении стандартных предположений о модели.

Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации:

. (2.32)

Средняя ошибка аппроксимации не должна превышать 8–10%.

Оценка значимости уравнения регрессии в целом производится на основе -критерия Фишера, которому предшествует дисперсионный анализ. Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной от среднего значения 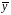раскладывается на две части – «объясненную» ( ) и «необъясненную» ( ).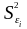

Случайные величины и имеют -распределение соответственно с (m-1) и (n-m) степенями свободы. Поэтому уравнение регрессии значимо на уровне α, если фактически наблюдаемое значение статистики

, (2.33)

где - сумма квадратов, объясненная моделью;

- остаточная сумма квадратов;

m – число оцениваемых параметров уравнения регрессии;

n – число наблюдений;

– табличное значение критерия.

В случае линейной парной регрессии m=2 и уравнение регрессии значимо на уровне значимости α, если

.