12) Расчеты на прочность и жесткость при кручении.

Прочность вала считается обеспеченной, если max напряжения τ_max в опасном сечении его не превышают допустимых.

Τ_max≤[τ_КР]. Опасным для вала с W_ρ=const будет то сечение, в котором Т(х) мах. Wρ  полярный момент сопротивления сечения вала.

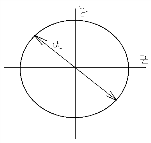
Iρ=πd⁴/32; Iy=Iz= πd⁴/64; Iρ=Iy+Iz; Wρ= Iρ/(d/2)= πd³/16=0.2d³

С условия прочности вытекает 3 типа задач:

1) проверочный расчет.

2) проектный расчет.

T(x)/Wρ≤ [τ_КР]; Wρ≥T(x)/[τ_КР]; πd³/16≥ T(x)/[τ_КР]; d≥³√(16T(x)/(π[τ_КР])) или d≥³√(T(x)/(0.2[τ_КР])).

Для кольцевого сечения:

Iρ=πD⁴/32 - πd⁴/32=(πd⁴/32)(1-e⁴);

C=D/d; Wρ=(πd³/16)(1-e³)

d≥ ³√ (16T(x)/(π(1-c³)[τ_КР])) или

d≥ ³√ (T(x)/(0.2(1-c³)[τ_КР])).

3) определение грузоподъемности:

из условия прочности имеем:

T(x)/Wρ≤ [τ_kp];

Расчет на жесткость: условие жесткости: φ=∫_LT(x)dx/GIρ≤[φ]; [φ]=(4…17)10^-3 рад/м. Если Т(х)=const и Iρ=const, то: φ=T(x)dx/GIρ≤[φ];

13)Условия прочности и жёсткости при кручении прямо бруса круглого (или кольцевого) поперечного сечения.

.

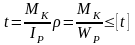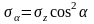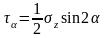15) Закон парности касательных напряжений.

, .

- закон парности касательных напряжений.

16) . Главные напряжения.

, .

18) экстремальными значениями для σ_α и σ_β являются главные напряжения, т.е. σ₂≤σ_α≤σ₁; σ₂≤σ_β≤σ₁. Касательные напряжения τ имеет максимальные величины на площадках α=±45º от направления σ₁. τ_α=-τ_β. Получили подтверждение закона парности касательного напряжения: τ на двух взаимно перпендикулярных площадках всегда равны по величине и противоположны по направлению.

Порядок решения задач методом Мора.

1) Для заданной балки на каждом участке записываем законы изменения M_F(x).

2) Освобождаем балку от внешней нагрузки.

3) В т. К по направлению искомого перемещения прикладываем единичную силу (момент) и для каждого участка записываем законы М₁(х).

4) Подставляем M_F(x), M₁(x) в интеграл Мора и вычисляем его. Если полученное Δ_KF имеет знак «–», то действительное перемещение точки имеет направление противоположное единичной силе.

19)Деформации при плоском напряженном состоянии. Обобщенный закон Гука.

Дано: σ₁ и σ₂.

Найти: ε₁ и ε₂, т.е. относительную деформацию бесконечно малого элемента в окрестности рассматриваемой точки.

ε₁=ε₁'+σ₁"; ε₂=ε₂'+σ₂", где ε₁' и ε₂' – результат действия σ₁;

σ₁" и σ₂" – результат действия σ₂.

Рассмотрим плоское деформированное состояние как сумму двух одноосных, для которых закон Гука: σ=Еε.

Продольная: ε_Х;

поперечная: ε_Y=-υε_X; ε_Z=-υε_X.

ε₁'=σ₁/E; σ₂"=σ₂/E;

20)Потенциальная энергия деформации. Гипотезы прочности.

U=∫(M²(x)dV/(2EI_z)); U равно половине произведения внешней силы на перемещение точки под этой силой (сумме произведений), что есть работа внешних сил на перемещениях точки под ними.

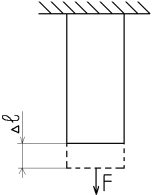
Для одноосного напряженного состояния:

U= ½FΔl; U=½FΔl/(Al)=σε/2= σ²/2E;

При трехосном (пространственном напряженном состоянии):

U=σ₁ε₁/2+σ₂ε₂/2+σ₃ε₃/3=(1/2E)(σ₁²+σ₂²+σ₃²-2υ(σ₁σ₂+σ₂σ₃+σ₃σ₁))

При деформации тела (пространственное) не только происходит изменение его объема, но и изменение формы (кубик → параллелепипед). U=U_V+U_Ф, где U_V – удельная потенциальная энергия изменения объема,

U_Ф – удельная потенциальная энергия формообразования (формоизменения).

U_V=(1-2υ/6E)(σ₁+σ₂+σ₃)²;

U_Ф=(1+υ/6E)((σ₁-σ₂)²+(σ₂-σ₃)²+(σ₃-σ₁)²);