
- •Теория квантовых переходов. Общее выражение для вероятности перехода из одного состояния в другое
- •Внезапное изменение взаимодействия
- •Переходы под действием периодического возмущения
- •Поглощение и излучение света. Вероятность перехода.
- •Спонтанное и индуцированное излучение. Коэффициенты Эйнштейна.
- •Время жизни возбужденного состояния атома
- •Принцип соответствия
- •Правило отбора для гармонического осциллятора. Интенсивность излучения
- •Правило отбора для оптических электронов в атоме
- •Релятивистская квантовая механика Элементарные частицы в квантовой механике. Уравнение Клейна-Гордона. Релятивистское уравнение для частицы с нулевым спином
- •Уравнение Дирака
- •Решение уравнения Дирака для свободных частиц
- •Состояния с отрицательной энергией. Понятие об электронно-позитронном вакууме
- •Момент количества движения электрона в теории Дирака. Спин. Полный момент импульса. Шаровые спиноры.
- •Релятивистские поправки к движению электрона в электромагнитном поле. Уравнение Паули. Спиновый магнитный момент
- •Атом водорода с учетом спина электрона. Энергетические уровни. Правила отбора с учетом спина электрона. Тонкая и сверхтонкая структура
- •Ковариантная форма уравнения Дирака
- •Зарядовое сопряжение. Частицы и античастицы
- •Уравнения Дирака для частицы с нулевой массой покоя. Нейтрино. Спиральность и инвариантность нейтрино относительно операции комбинированной инверсии. Срт- инвариантность.
- •Атом во внешнем магнитном поле. Нормальный и аномальный эффекты Зеемана.
- •Атом во внешнем электрическом поле. Эффект Штарка.
- •Квантовые системы, состоящие из одинаковых частиц
- •Симметричные и антисимметричные волновые функции. Схемы Юнга.
- •Теория основного состояния атомов с двумя электронами
- •Возбужденные состояния атома гелия. Орто- и парагелий
- •Вариационный метод Ритца
- •Метод самосогласованного поля Хартри — Фока
- •Адиабатическое приближение
- •Основные виды химической связи
- •Молекула водорода.
- •Теория валентности
- •Силы Ван-дер-Ваальса.
- •Энергетические уровни двух-атомных молекул.
- •Теория упругого рассеяния
Уравнение Дирака
1. нельзя интерпретировать как плотность вероятности нахождения частицы, эта величина определяется не только начальным зарядом ВФ но и начальными значениями производной
2. Релятивистское УШ должно содержать первые производные ВФ по координате
3. Принцип суперпозиции состояний. Волновое уравнении должно быть линейным
На основе этих соображений для описания движения свободной частицы Дираком было сформулировано следующее уравнение
![]() (1)
(1)
![]() (2)
(2)
(3)
Оно имеет полное, хотя и формальное, сходство с УШ. Чтобы был оператор гамильтона, необходимо чтобы для него существовало такое же соотношение как для энергии и импульса в релятивистской теории
![]()
![]() (4)
(4)
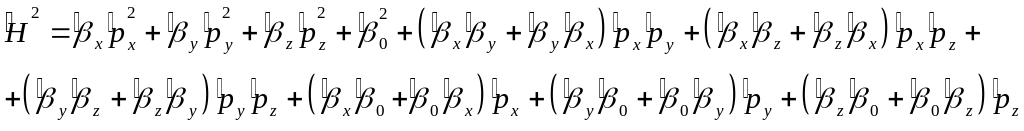 (5)
(5)
![]()
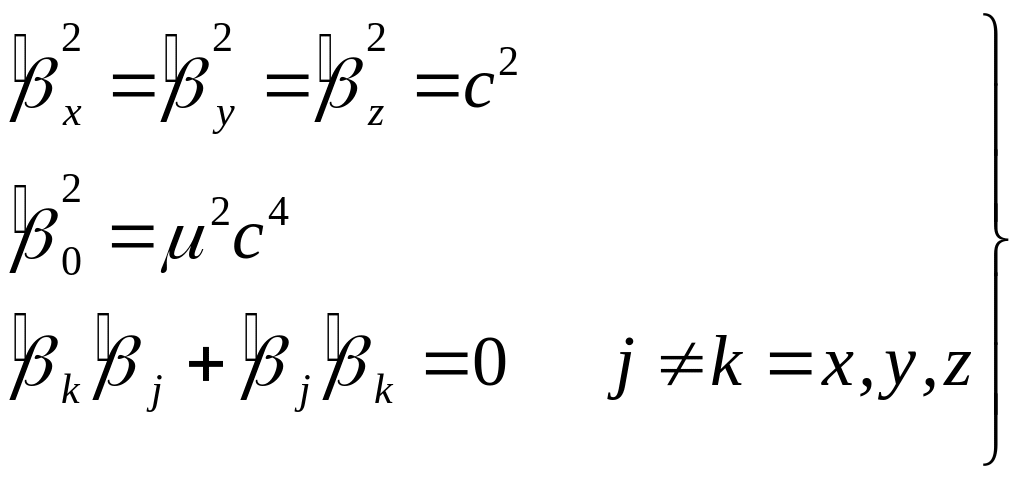 (6)
(6)
![]()
![]()
![]() (7)
(7)
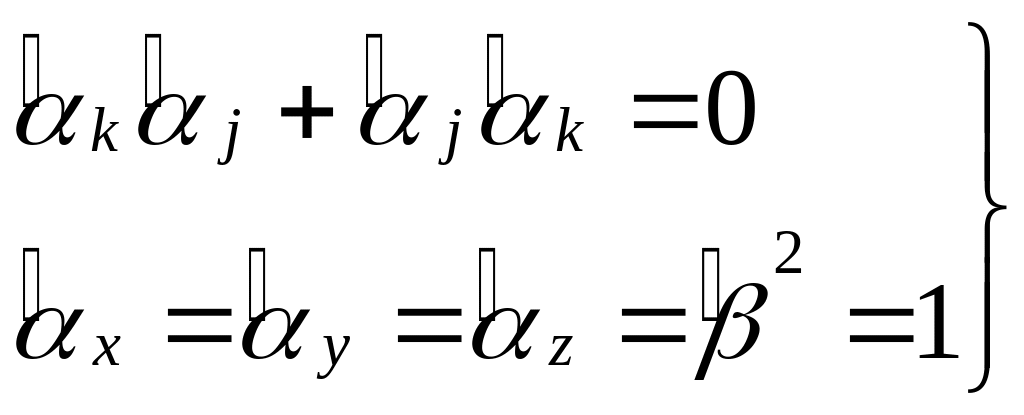 (8)
(8)
![]()
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
Заметим, что действие тех операторов не могут сводиться к умножению ВФ на некоторые числа. С помощью операторов, сводящихся к случайным числам невозможно было бы сводить к этим соотношениям. Но существует определенный класс операторов, который представляет собой числа, но удовлетворяет соотношением. Это матрицы. Будем искать среди квадратичных матриц
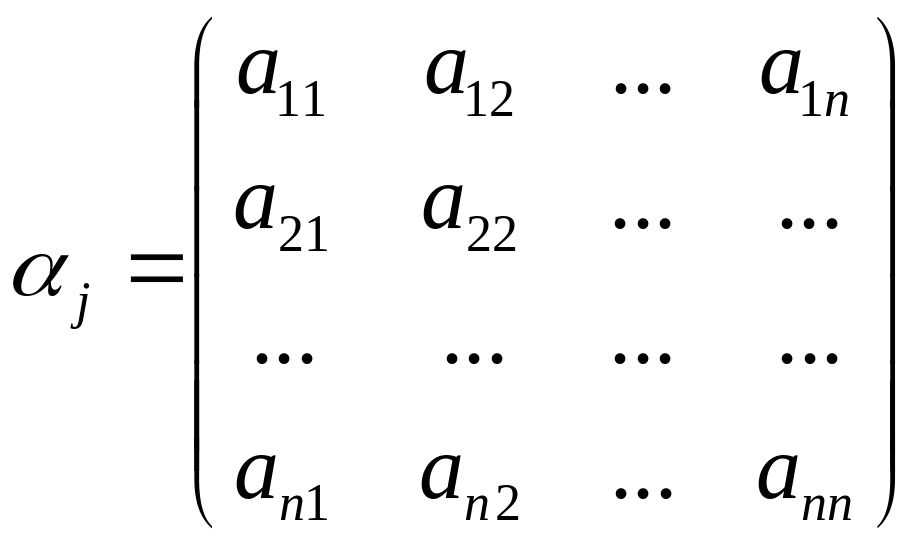 (13) В общем случае это комплексные
числа. Определим число n.
Будем считать что все матрицы одинакового
порядка. Сопоставим этим матрицам
определитель
(13) В общем случае это комплексные
числа. Определим число n.
Будем считать что все матрицы одинакового
порядка. Сопоставим этим матрицам
определитель
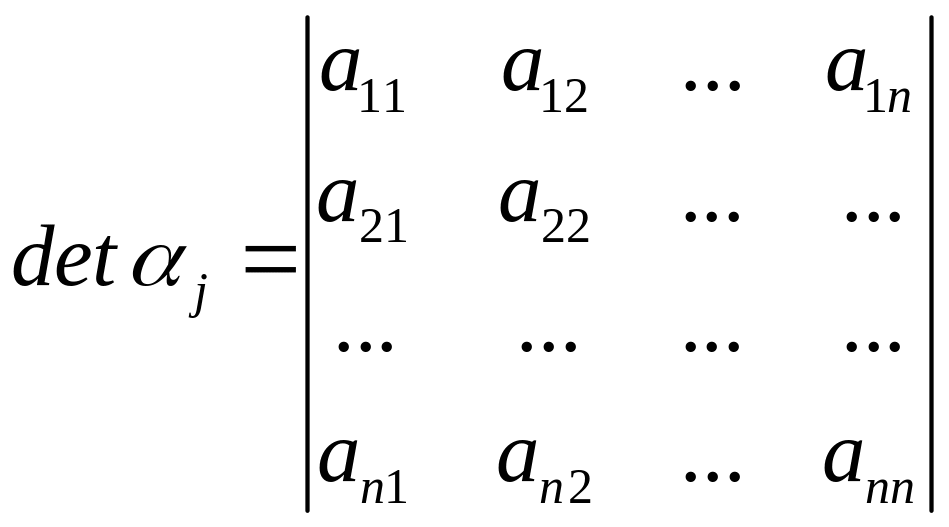 Прежде всего отметим свойства матриц
Прежде всего отметим свойства матриц
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
![]()
Если n=2 то матрицы второго порядка. Пример двухрядных матриц = матрицы Паули
![]()
![]() (17)
(17)
![]()
![]() (18)
(18)
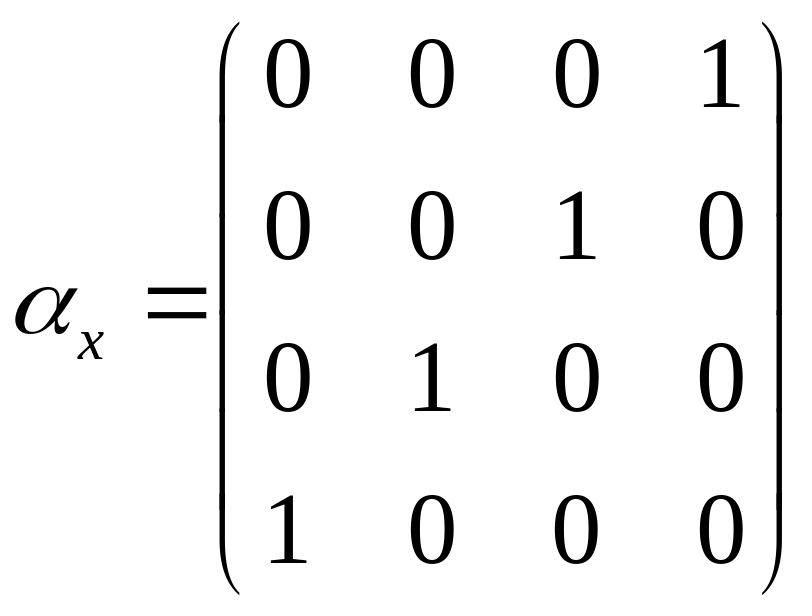
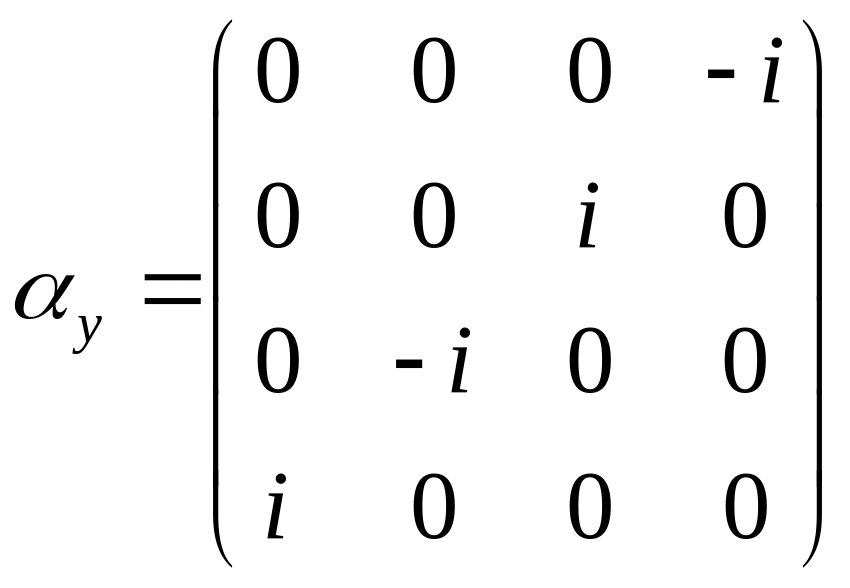
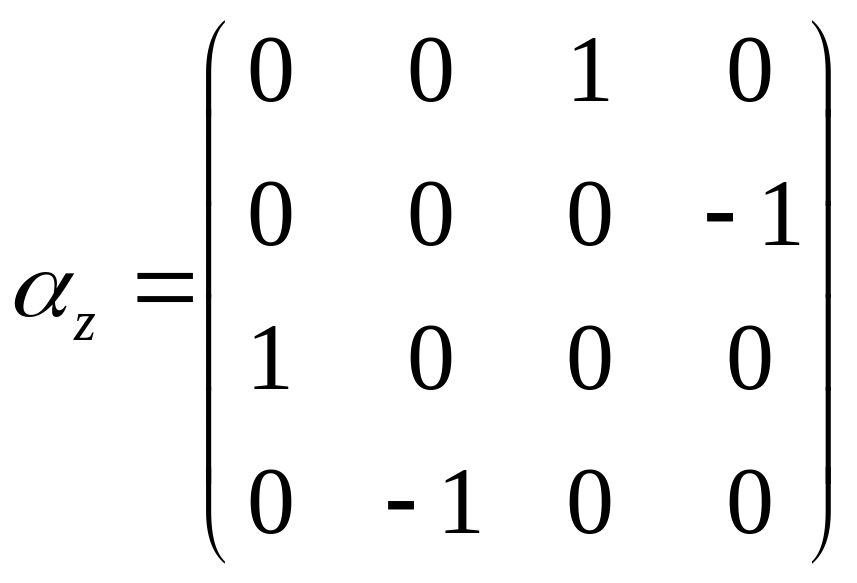
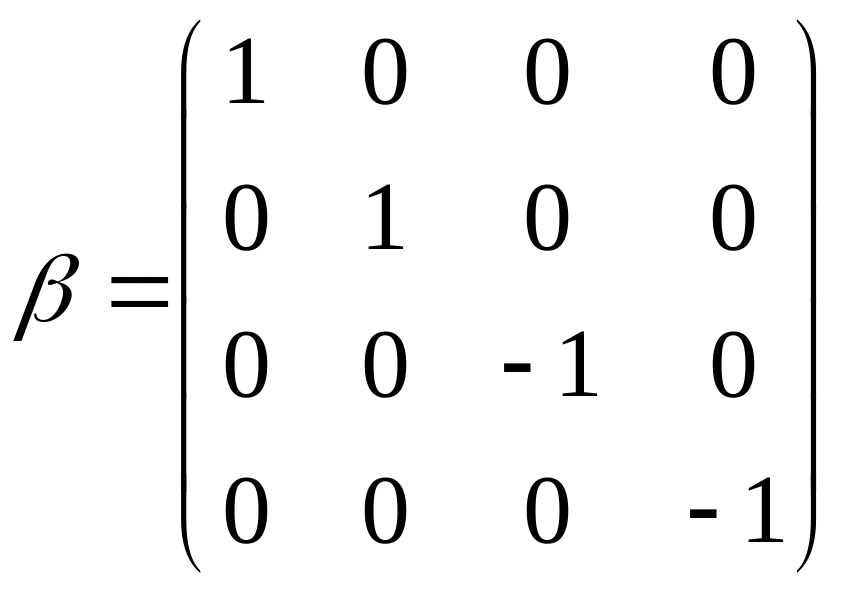 (19)
(19)
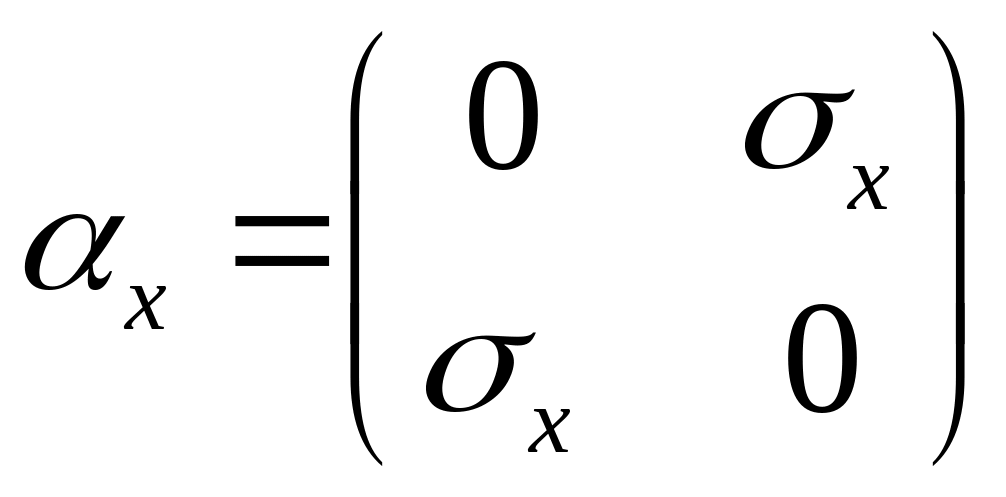
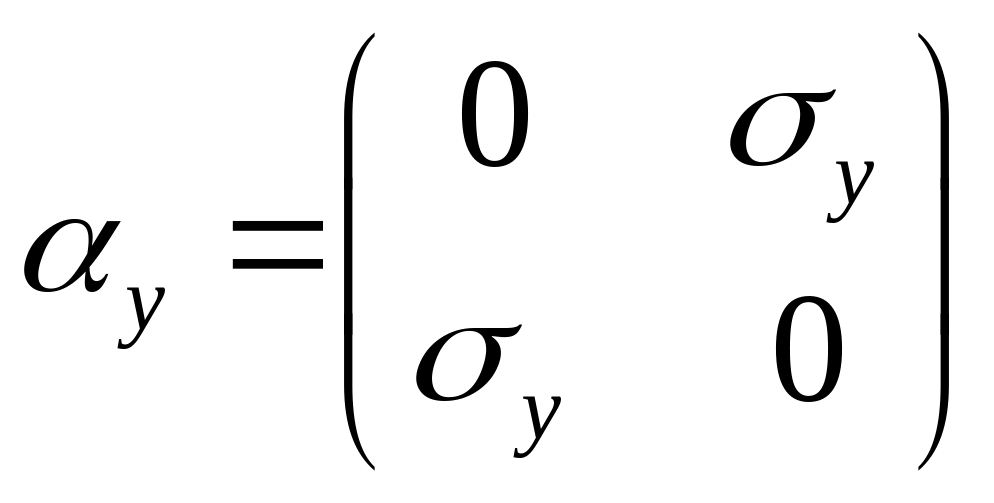
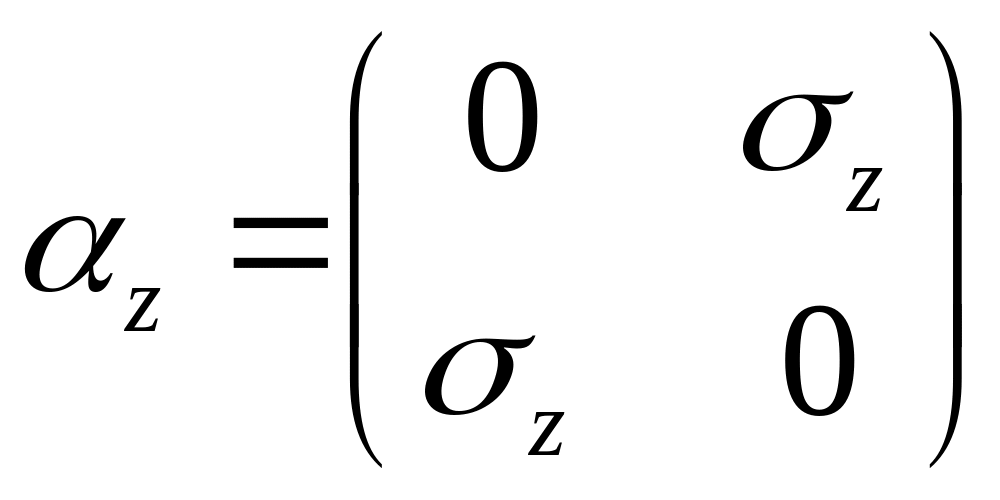
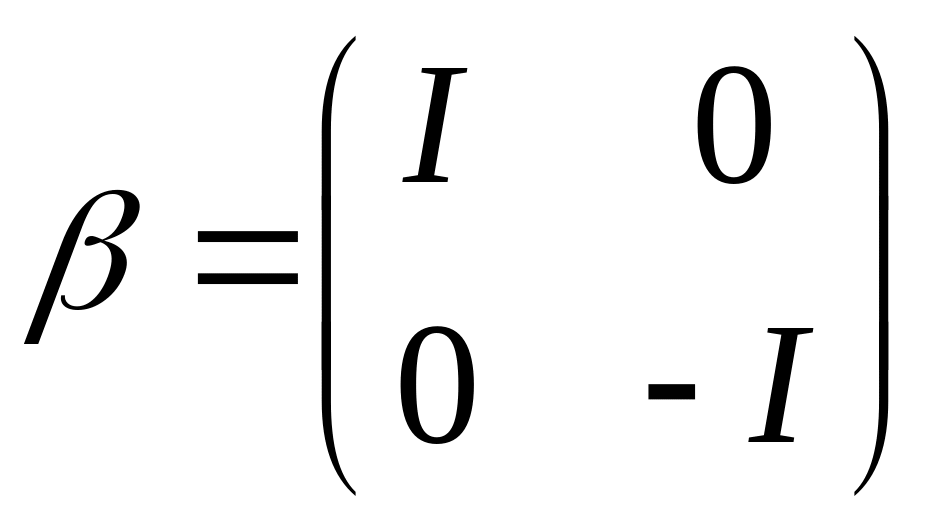 (20)
(20)
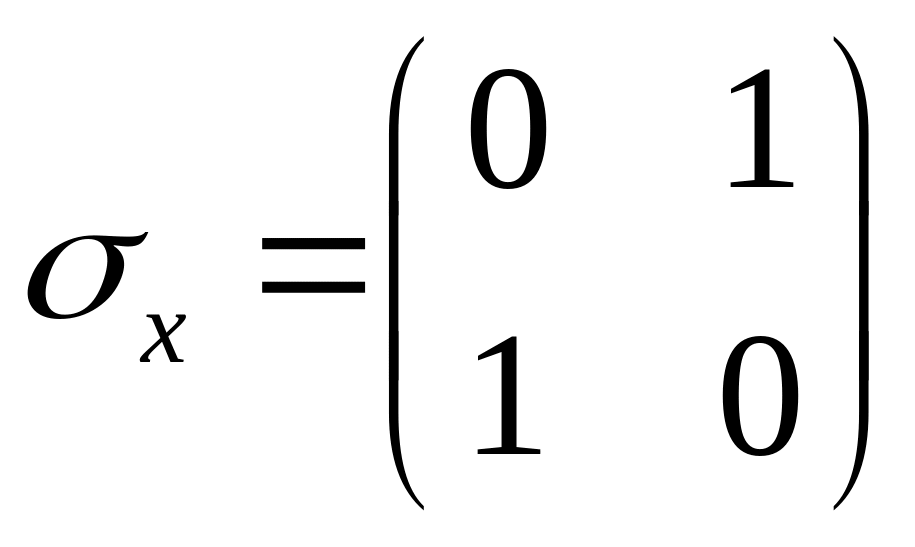
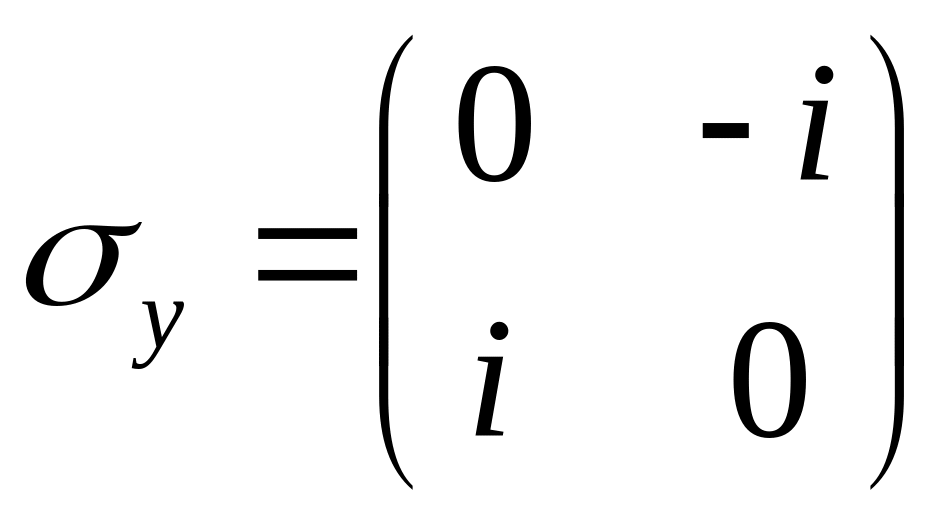
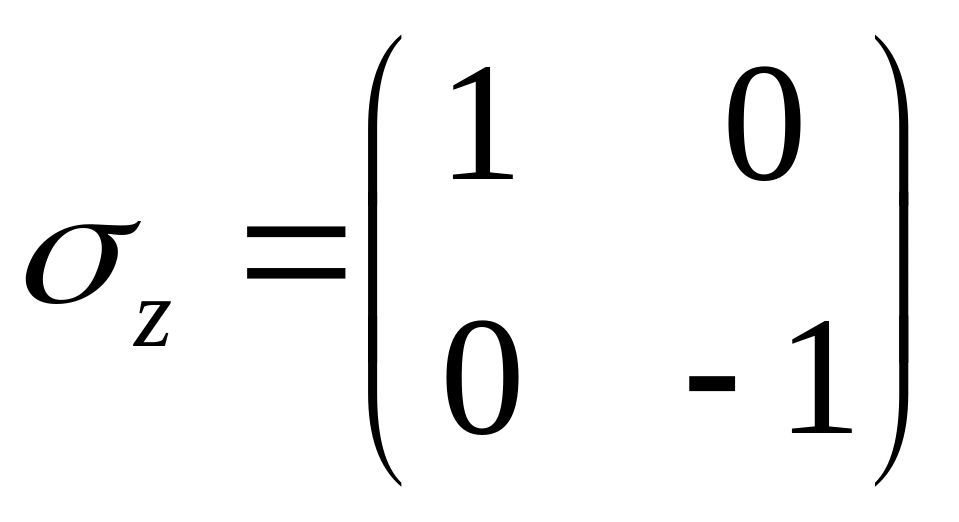 (21)
(21)
![]()
![]() (22)
(22)
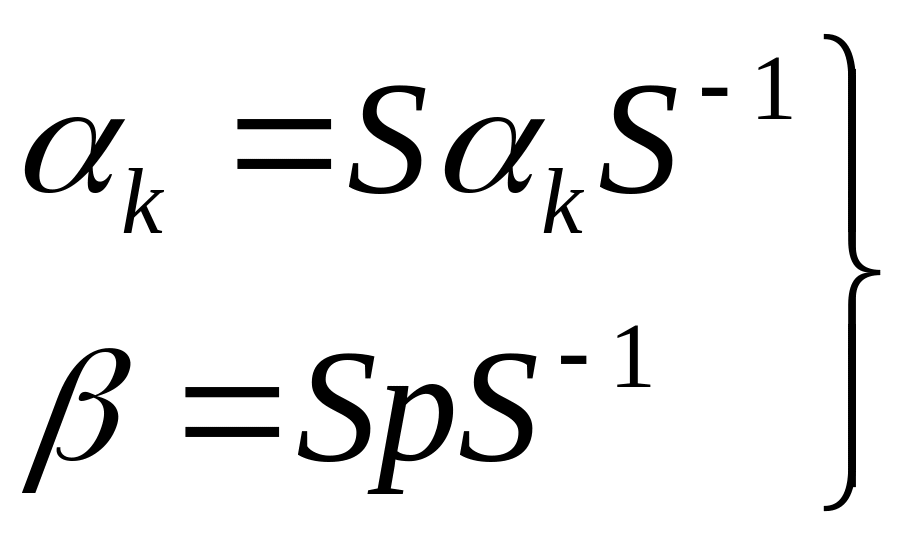 (23)
(23)
Где
![]() унитарная матрица
унитарная матрица
![]() .
Также удовлетворяют соотношениям
антикоммутации а также их квадрат равен
I. Причем необходимо
отметить, что все физические следствия
удовлетворяют уравнениям Дирака и не
зависят от набора матриц. Так как матрицы
и
четвертого порядка, ВФ
должна быть четырехкомпонентной. Запишем
в виде столбца
.
Также удовлетворяют соотношениям
антикоммутации а также их квадрат равен
I. Причем необходимо
отметить, что все физические следствия
удовлетворяют уравнениям Дирака и не
зависят от набора матриц. Так как матрицы
и
четвертого порядка, ВФ
должна быть четырехкомпонентной. Запишем
в виде столбца
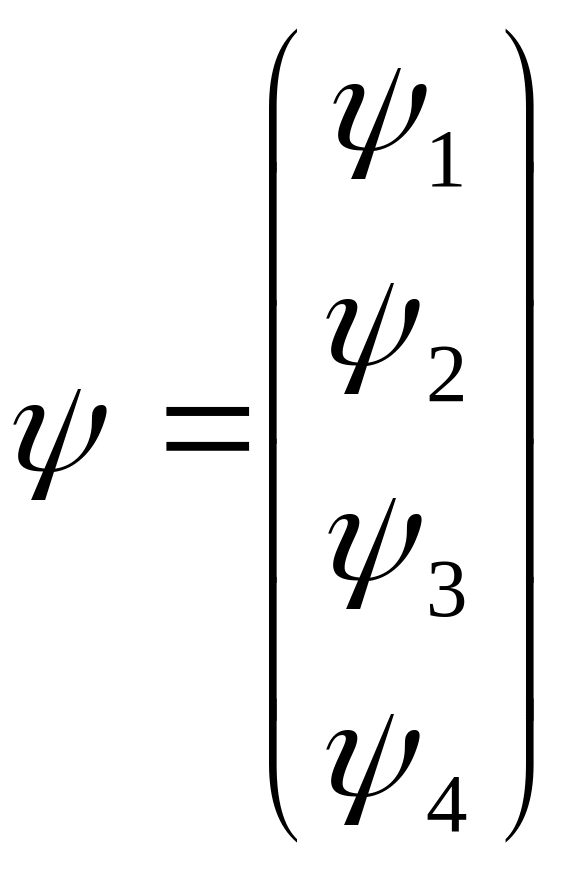
![]()
Тогда уравнение Дирака (матричное) будет эквивалентно четырем уравнениям
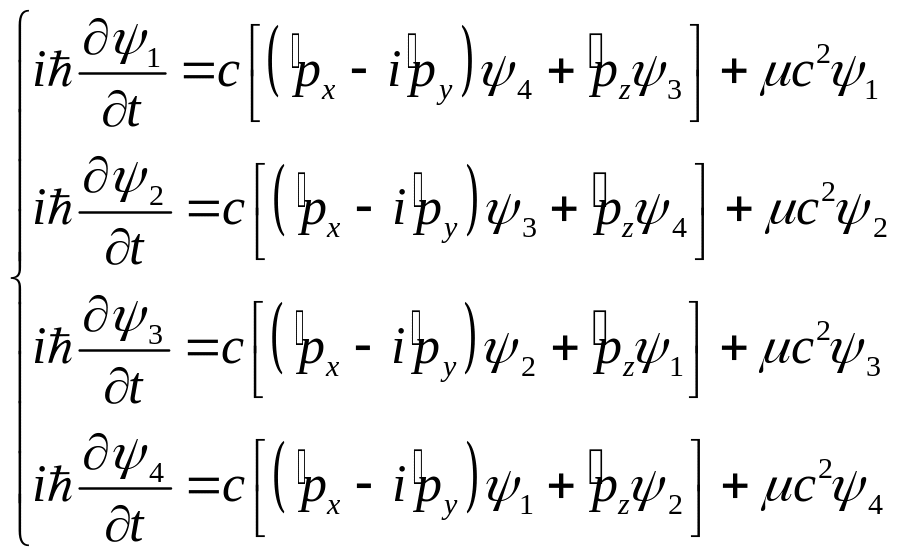 (25)
(25)
Для того чтобы записать уравнение
Дирака, описывающее движение заряженной
частицы во внешнем электрическом поле,
необходимо оператор импульса
![]() заменить на канонический оператор
заменить на канонический оператор
![]() .
Тогда справа умножится на скалярный
потенциал
.
Тогда справа умножится на скалярный
потенциал
![]()
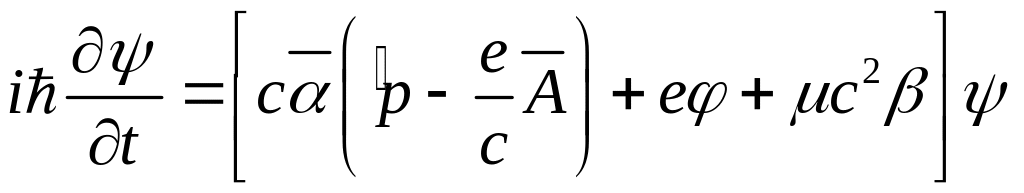 (26)
(26)
Вернемся к уравнению Дирака для частицы, движущейся свободно
![]() (9)
(9)
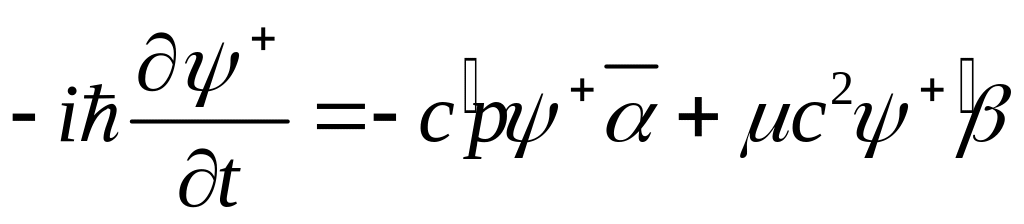 (9’)
(9’)
Произведем действие
![]()
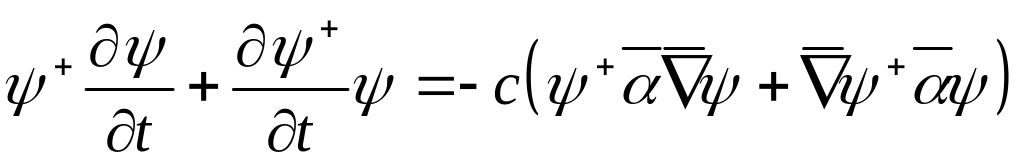
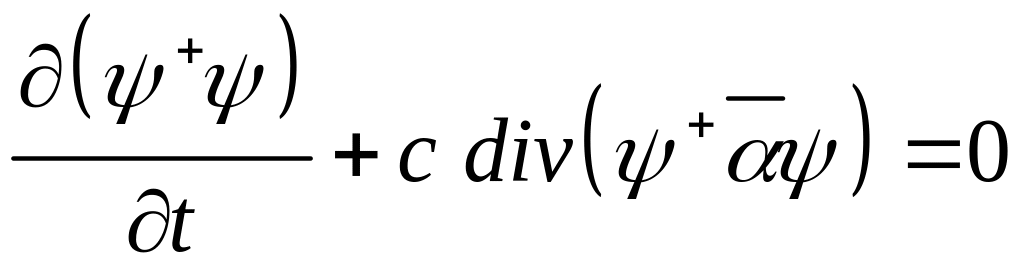 (27)
(27)
То есть мы пришли к уравнению непрерывности.
![]() - плотность вероятности положения
частицы в той или иной точке пространства,
так как сугубо положительная величина
- плотность вероятности положения
частицы в той или иной точке пространства,
так как сугубо положительная величина
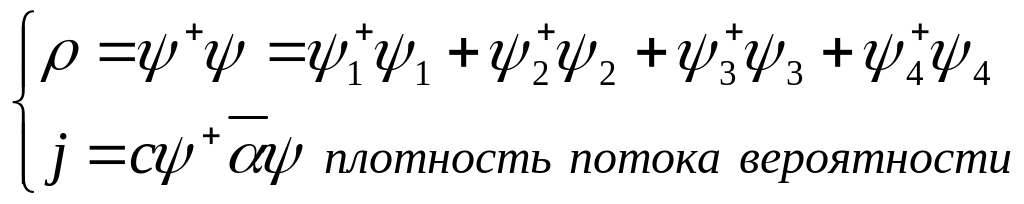 (28)
(28)
Таким образом, как и в теории Шредингера ВФ допускает обычную вероятностную интерпретацию, а если так, то значит остаются в силе все основные положения квантовой механики
1. Интерпретация величины
![]() ,
где
,
где
![]() коэффициент разложения ВФ в ряд по СФ
некоторого самосопряженного оператора
коэффициент разложения ВФ в ряд по СФ
некоторого самосопряженного оператора
![]()
2. Определение среднего значения
![]()
вся схема построения квантовой механики справедлива для уравнения Дирака, то есть Дирак получил уравнения, которые не противоречили основным положениям квантовой механики
