Спонтанное и индуцированное излучение. Коэффициенты Эйнштейна.

Вероятность испускания фотона в единицу времени при переходе системы из пропорционально числу фотонов в единице объема в э/м волне, взаимодействующей с этой системой, поэтому выражение (21) для вероятности излучения называется вероятностью вынужденного или индуцированного излучения

Вероятность поглощения в единицу времени фотона при переходе атомной системы из . Если свет, имеющий поляризацию поглощается из телесного угла , то соответствующая вероятность поглощения

(1)

Если электромагнитное излучение находится в равновесии с черным телом, при температуре , то число фотонов вероятности поглощения на среднее число фотонов при данной температуре

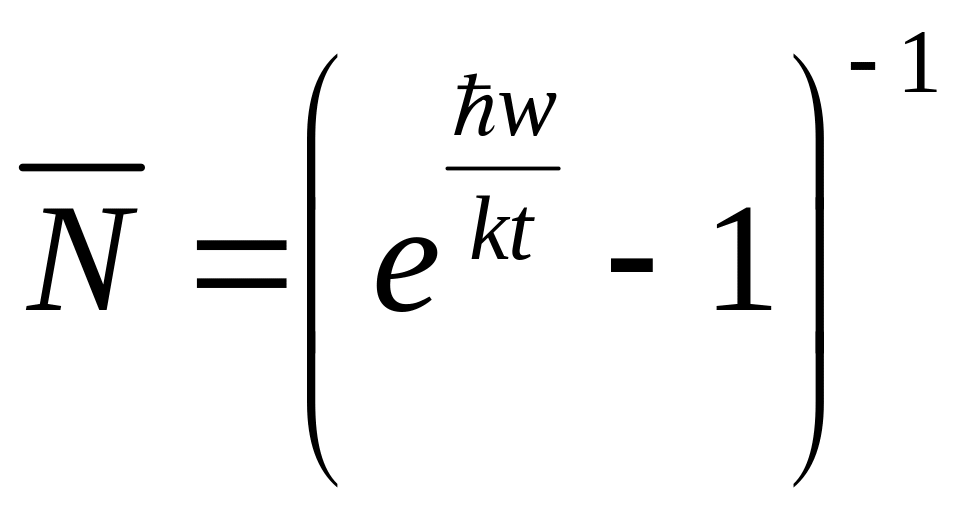
В этом случае направление излучения и поляризации произвольные, поэтому в формулах для вероятности нужно провести соответствующее суммирование, чтобы получить вероятность, отнесенную в единицу времени полного поглощения фотона.

(3) вероятность испускания

(4) вероятность поглощения

Эйнштейн показал, что статистическое равновесие между излучением и поглощением возможно только в случае когда наряду с вынужденным излучением, которое пропорционально плотности излучения имеется спонтанное излучение, происходящее и в отсутствии внешнего излучения, то есть система сама находится в возбужденном состоянии и с течением времени переходит в более низшее состояние

Спонтанное излучение связанно с взаимодействием атомной системы с нулевыми колебаниями электромагнитного поля.

Согласно теории квантования, вероятность спонтанного излучения получается из выражения (2). Если мы приравняем единице

(5)

Общее выражение для общей (суммарной) вероятности испускания фотона в единицу времени. при переходе будет определяться формулой

(6)

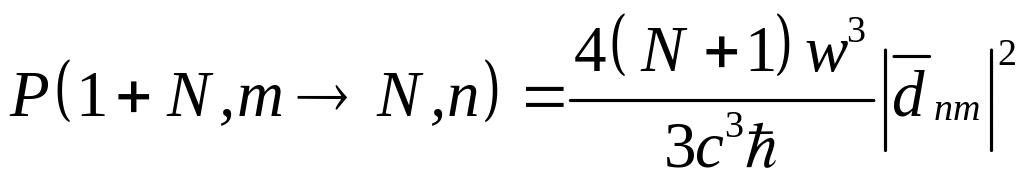(7)

Вероятность спонтанного перехода из в единицу времени с излучением кванта света частоты внутри телесного угла с поляризацией

(8)

Если имеется излучение, воздействующее на атом, то оно оказывает двоякое воздействие. Это излучение может поглощаться, тогда атом будет переходить в высшее состояние. Вероятность поглощения . Во-вторых, если атом находится в возбужденном состоянии, то внешнее возбуждение может способствовать переходу в низшее состояние, так что вероятность поглощения увеличивается до (вероятность индуцированного излучения).

(9), - вероятность поглощения, - вероятность излучения.

По предположению Эйнштейна, вероятность пропорциональна числу квантов света как раз того сорта, о поглощении излучения которых идет речь.

Излучение может быть немонохромным, иметь различные направления распределения и различную поляризацию. Для определения характера излучения вводится величина , которая дает плотность энергии излучения, имеющего поляризацию , направление распределения в пределах телесного угла и частоту, лежащую в интервале . Так как энергия кванта , то число квантов света, частота которых лежит в этом интервале и имеют поляризацию равна . В основе предположения Эйнштейна о пропорциональности числа квантов и вероятности излучения мы можем записать вероятность поглощения в следующем виде:

(10)

(11)

Величины , , , называются дифференциальными коэффициентами Эйнштейна. Они зависят только от рода системы излучающей или поглощающей. Пусть число атомов в нижнем состоянии , а число атомов в верхнем (возбужденном) состоянии , тогда число квантов, излучаемых в 1 секунду при переходе будет равно . Соответственно поглощаемых в 1 секунду . Равновесие будет, когда число поглощенных квантов будет равно числу излученных

Допустим мы имеем дело с тепловым равновесием. Тогда число атомов, находящихся в различных состояниях будет функциями температуры.

Согласно каноническому распределению как для канонических так и для атомных систем число атомов, находящихся в состоянии

(15)

Если то есть неограниченно нагревать, то плотность излучения , отсюда

(16)

(17)

Разлагая в ряд получаем формулу Рэлея-Джинса

(18)

(19)

(20)

Согласно теории Эйнштейна вероятность поглощения света с энергией

Волна плоская и распределяется в определенном направлении, поэтому в формулировку входит лишь спектральное распределение, а здесь по углам. Общая связь между спектральным распределением и угловым

(21)

Величина спектра конечна, а распределение по углам отлична от нуля для одного определенного направления. В этом случае плотность (22)

Вероятность поглощения (23)

На основе закона сохранения энергии вероятность поглощения света с энергией должна быть равна вероятности перехода из состояния , то есть

Вероятность спонтанного излучения 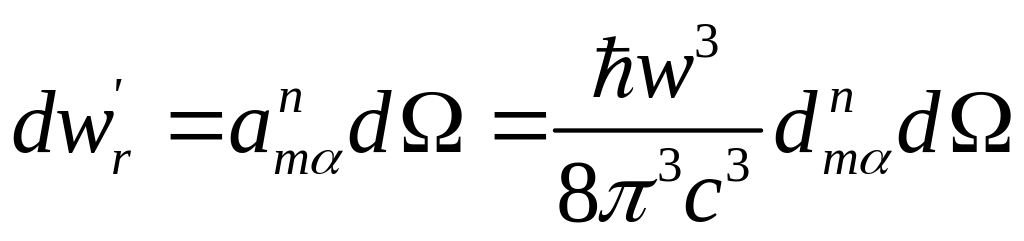(25)

(26)

(27)

Если уровни и вырождены, то таких переходов, имеющих матричный элемент много.

(28) коэффициенты Эйнштейна

Излучение света частотой в единицу времени

Коэффициент для поглощения неполярного излучения частотой

(29)

- степень вырожденности уровня с энергией

Таким же образом вводят коэффициенты индуцированного излучения

(30)