Силы Ван-дер-Ваальса.
Помимо рассматриваемых
валентных сил, между атомами и молекулами,
находящимися на больших расстояниях
друг от друга происходят слабые
взаимодействия. Они имеют характер
притяжения- силы Ван- дер- Ваальса.
Рассмотрим упрощенный подход на примере
взаимодействия двух осцилляторов. Пусть
два осциллятора с молекулами 
и 
находятся на расстоянии 
:
значительно больше 
и 
.
Найдём потенциальную энергию взаимодействия
:
Т.к. 
:
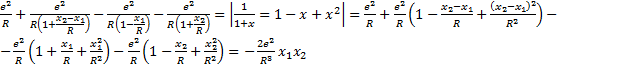(1)
По классической теории, в
случае, когда оба осциллятора не
колеблются: 
,
взаимодействие между ними отсутствуют
и 
.
Согласно квантовой механике должны
существовать нулевые колебания. Это
приводит к тому, что взаимодействие
осцилляторов не происходит даже когда
они не возбуждены. Рассмотрим свободные
колебания двух гармонических осцилляторов,
между которыми действуют притяжения
вида (1)
(2)- уравнение для нахождения стационарных
состояний.
,(3)
где 
.
В случае отсутствия взаимодействия энергия равна энергии осциллятора и равна:
(4)
В отсутствии возбуждения
мы имеем энергию нулевых колебаний:
(5),
-
амплитуда нулевых колебаний.
При учёте взаимодействия введём нормированные координаты:
,
(6)
(7)
Можно осуществить разделение переменных.
(8)
,
(9)
– разложим в ряд по 
:
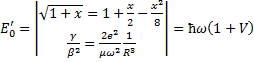(8)
Где 
потенциальная
энергия Ван-дер-Ваальсовских сил, которая
имеет квантовую природу.
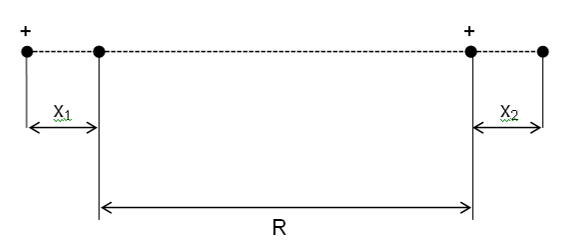
Рассмотрим теперь более общий вывод выражения для Ван-дер-Ваальсовских сил. Рассмотрим два атома, находящиеся на большом расстоянии; благодаря сферической симметрии атомы не имеют среднее значение дипольных моментов, но недиагональные матричные элементы дипольного момента отличны от нуля. Наглядно можно представить дипольный момент атома, как результат квантово-механического движения электронов, приводящий к появлению исчезновению дипольного момента в каждом моменте времени. В результате, у каждого атома индуцируются также дипольные моменты. Энергия (Ван-дер-Ваальсовских сил) взаимодействия атомов может вычислена на основе теории возмущения.
(11)
Здесь 
дипольные моменты атомов, 
единичный
вектор, взятый вдоль направления,
соединяющий центры диполей, 
расстояния между диполями.
Поправка к энергии первого
порядка есть:
(12)
Т.к. 
и 
Во втором порядке теории возмущения:
(13)
Здесь величина 
(14)
всегда
отрицательна.
(15)- выражает закон
взаимодействия Ван-дер-Ваальсовских
сил. Это взаимодействие не имеет
специфического характера, в том смысле,
что оно эквивалентно силам притяжения
убывающим как 
.
Для всех атомов не зависит от природы.
Силы Ван-дер-Ваальса убывают на
бесконечности достаточно быстро, но не
экспоненциально закону, как валентные
силы. Это приводит к тому, что межмолекулярные
силы заметны не только на расстоянии
порядка молекул, но и намного больших
расстояниях. Силы Ван-дер-Ваальса в
отличие от валентных сил обладает
свойством аддитивности. Если во
взаимодействии вступают не два, а три
и более атомов, то энергия взаимодействия
системы получается сложением энергии
полного взаимодействия. Если атомы
находятся не в 
состоянияя,
то они могут иметь отличные от нуля
средние значения квадрупольного момента.
В этом случае, кроме сил Ван-дер-Ваальса
между атомами будет иметь место
квадруполь-квадрупольное взаимодействие
(убывающее как 
).