
- •3. Модуль контроль (контрольні питання до дисципліни, для самоконтролю та самоперевірки) Модуль контроль (підсумковий) – 1 семестр
- •Модуль контролю (підсумковий) – 2 семестр
- •Модуль контролю (підсумковий) – 3 семестр
- •4. Зміст завдань самостійної роботи , індз та запитань для самоперевірки її виконання
- •Змістовий модуль 1.
- •Знайти матрицю , якщо , .
- •Обчислити:
- •Змістовий модуль 2.
- •Змістовий модуль 3.
- •Змістовий модуль 5.
- •Змістовий модуль 6.
- •1. Продиференціювати функцію:
- •Змістовий модуль 7.
- •Змістовий модуль 8.
- •Змістовий модуль 9.
- •Змістовий модуль 10.
- •Змістовий модуль 11.
- •5. Тематика індз Елементи лінійної алгебри
- •Обчислити визначники:
- •Знайти обернену матрицю до матриць:
- •Обчислити ранг матриці:
- •Теорія границь
- •Застосування похідної
- •Невизначений інтеграл
- •Вища математика
- •І семестр
- •Змістовий модуль 4. Теорія поверхонь
- •Іі семестр Змістовий модуль 5. Функції однієї змінної
- •Змістовий модуль 6. Диференціальне числення функції
- •Змістовий модуль 10. Ряди
- •Змістовий модуль 11. Диференціальні рівняння
- •Змістовий модуль 12. Елементи сферичної тригонометрії
- •7. Література до дисципліни Основна література
- •Додаткова література
4. Зміст завдань самостійної роботи , індз та запитань для самоперевірки її виконання
1-ий семестр
Змістовий модуль 1.
„Елементи лінійної алгебри”
Знайти матрицю
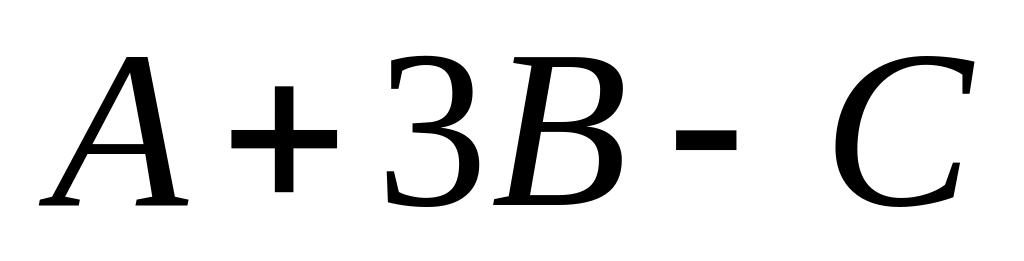 ,
якщо
,
якщо
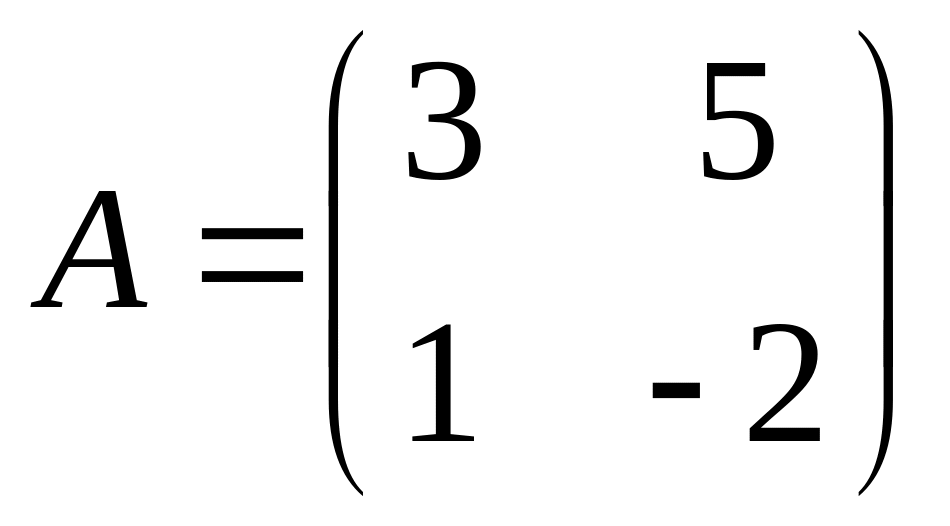 ,
,
 ,
,
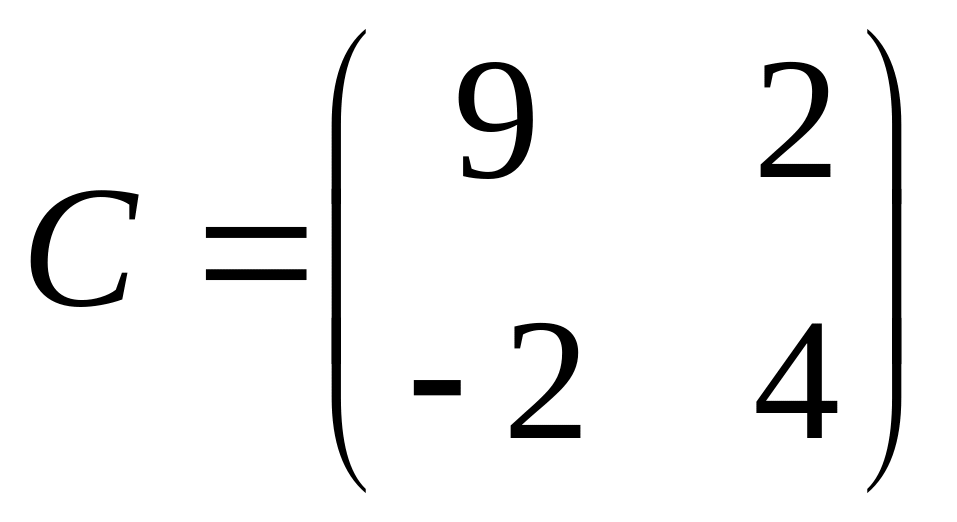 .
. ,
,
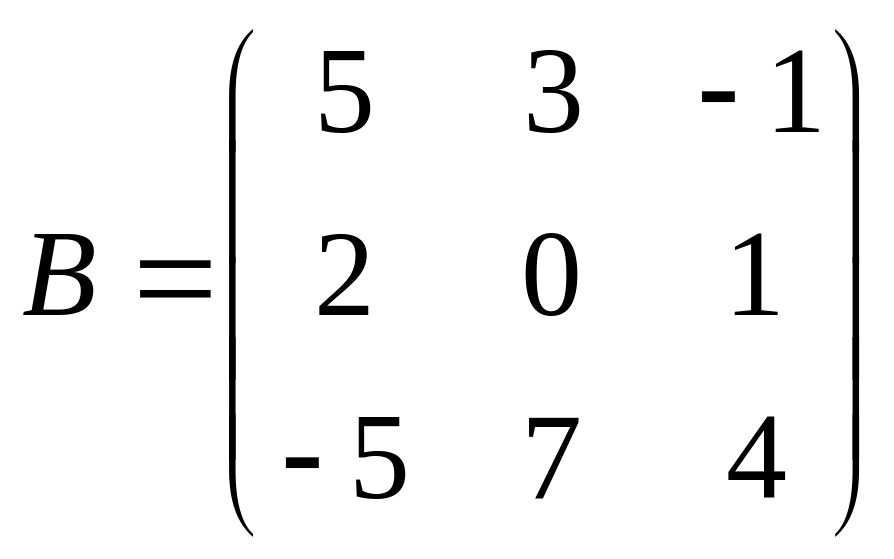 ,
,
 .
. ,
,
 ,
,
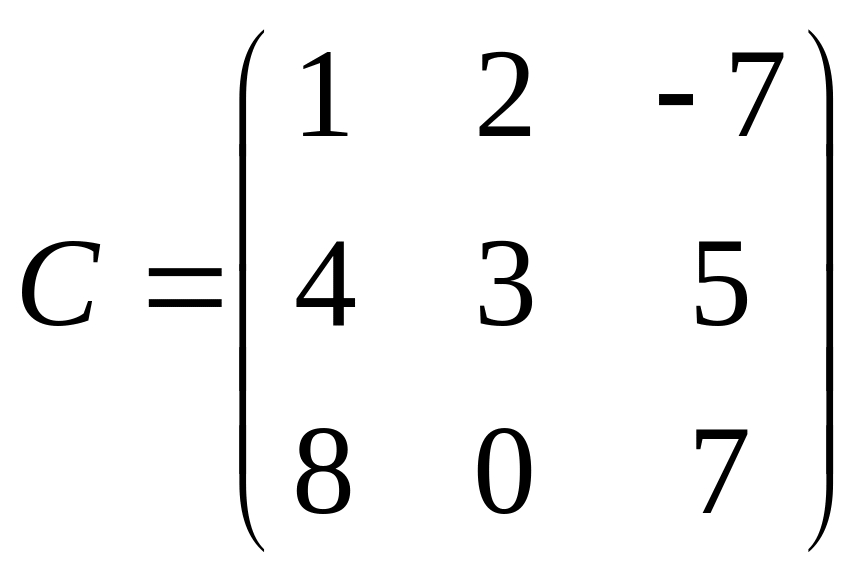 .
.
Знайти матрицю , якщо , .
Обчислити
 .
.Знайти добуток матриць АВ і ВА, якщо:
1)
![]() ,
,
![]() ; 2)
; 2)
![]() ,
,
![]() ;
;
3)
 ,
,
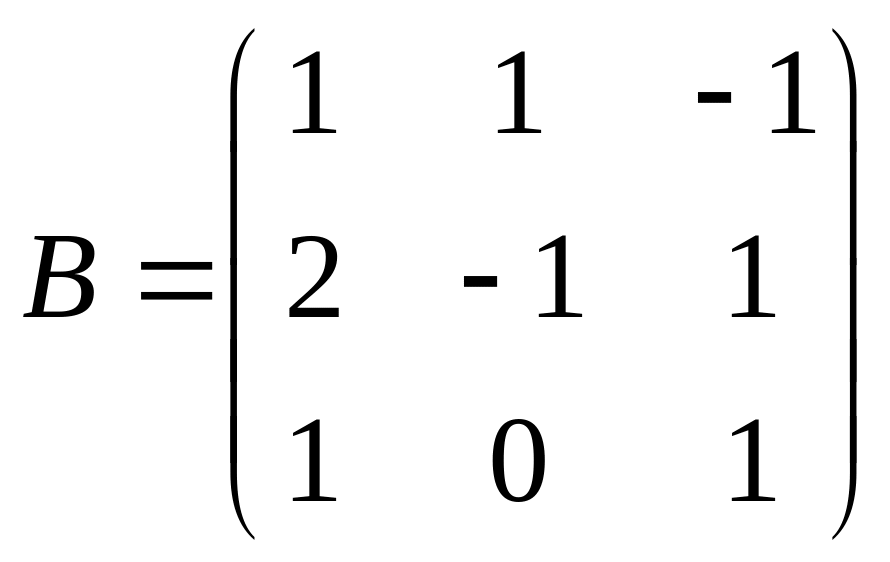 ; 4)
; 4)
 ,
,
![]() ;
;
5)
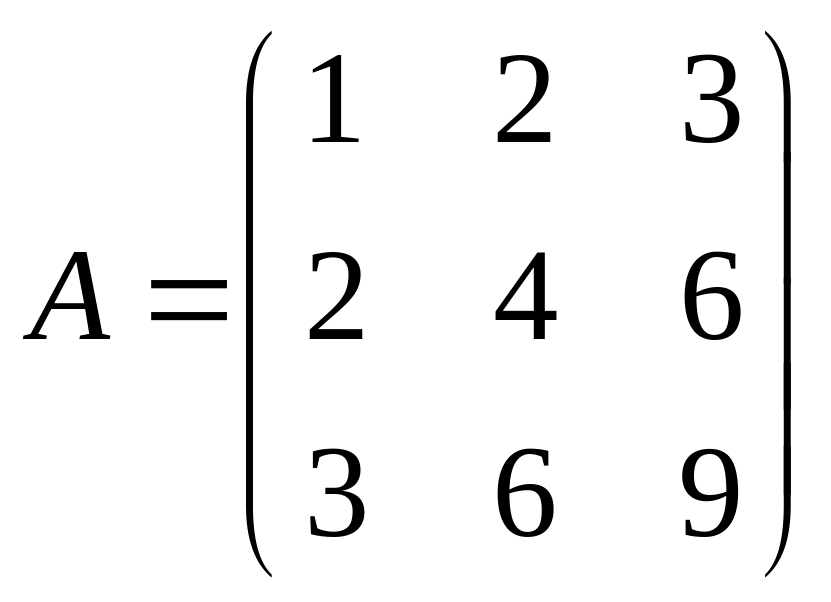 ,
,
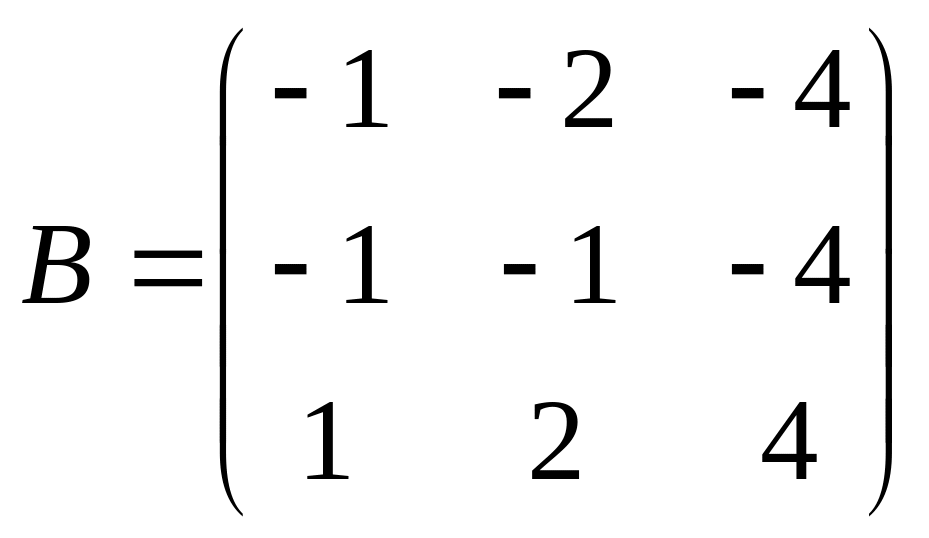 ; 6)
; 6)
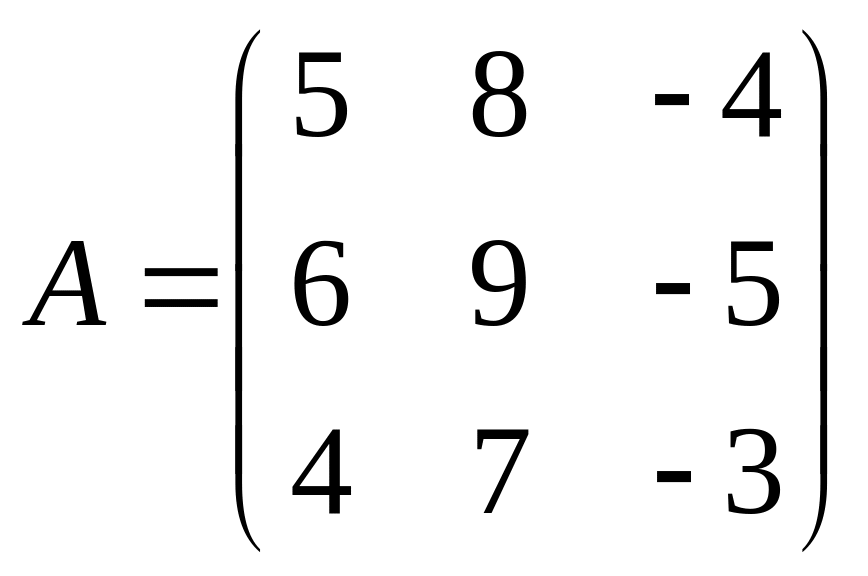 ,
,
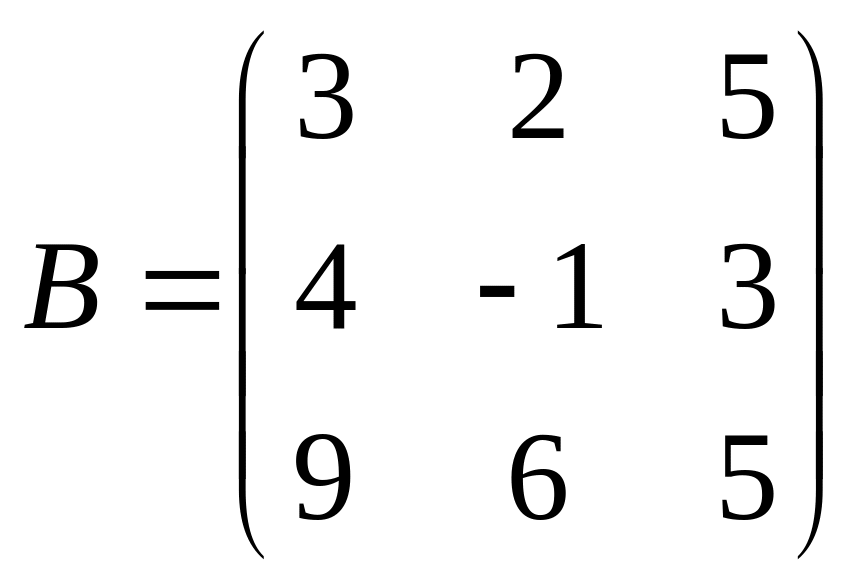 ;
;
7)
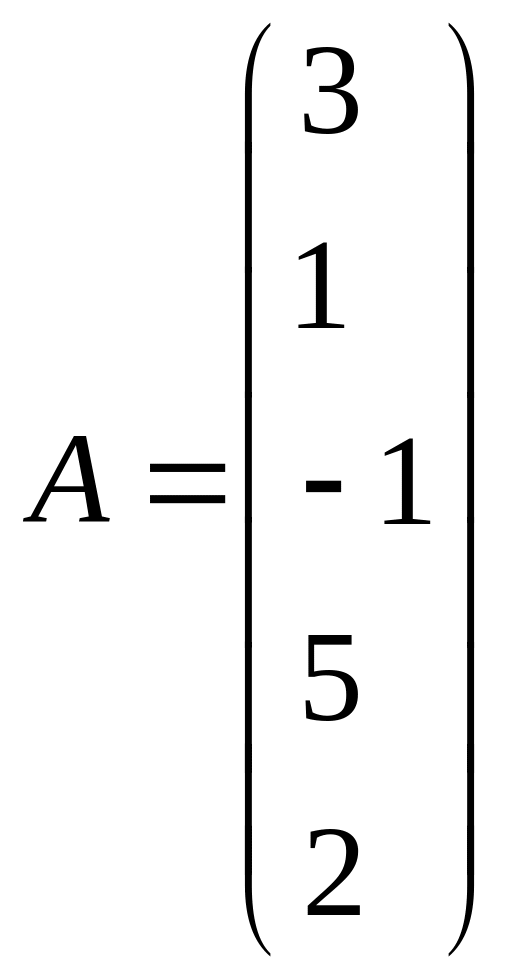 ,
,
![]() ; 8)
; 8)
 ,
,
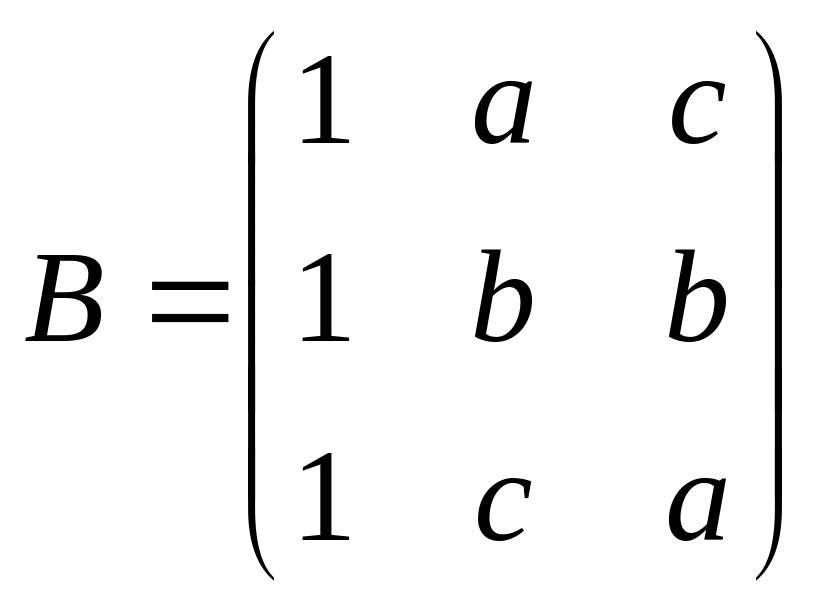 .
.
Обчислити:
1)
![]() ; 2)
; 2)
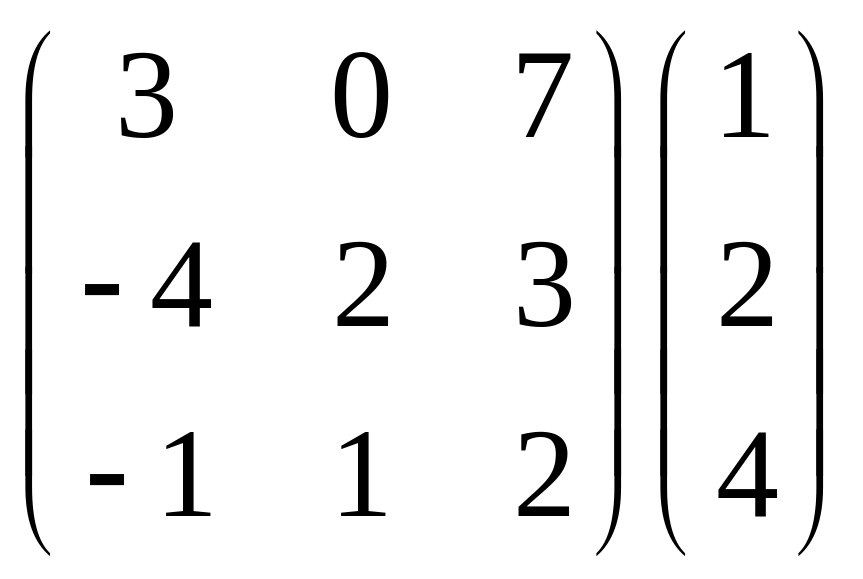 ;
3)
;
3)
 ;
;
4)
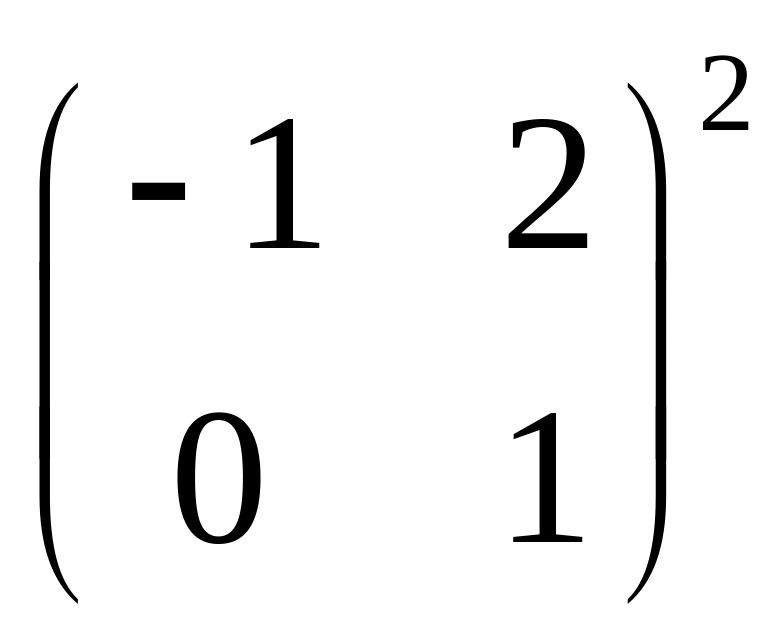 5)
5)
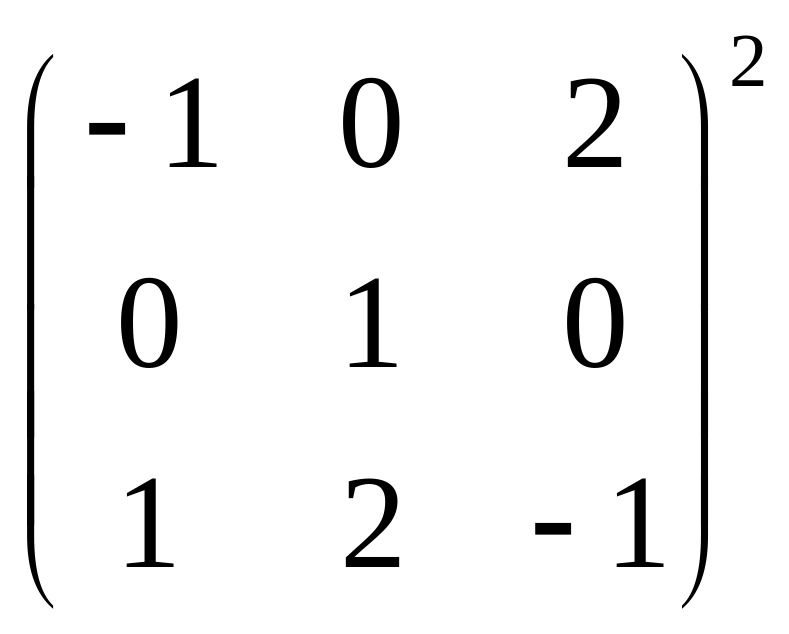 ; 6)
; 6)
 ; 7)
; 7)
 .
.
8)
![]() ,
якщо
,
якщо
![]() ;
9)
;
9)
![]() ,
якщо
,
якщо
 .
.
Обчислити визначники:
1)
![]() ;
2)
;
2)
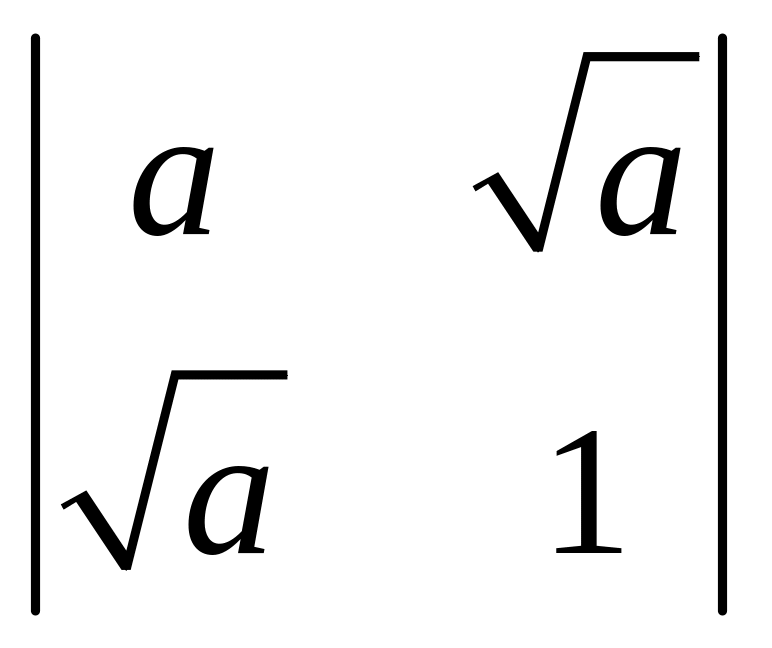 ;
3)
;
3)
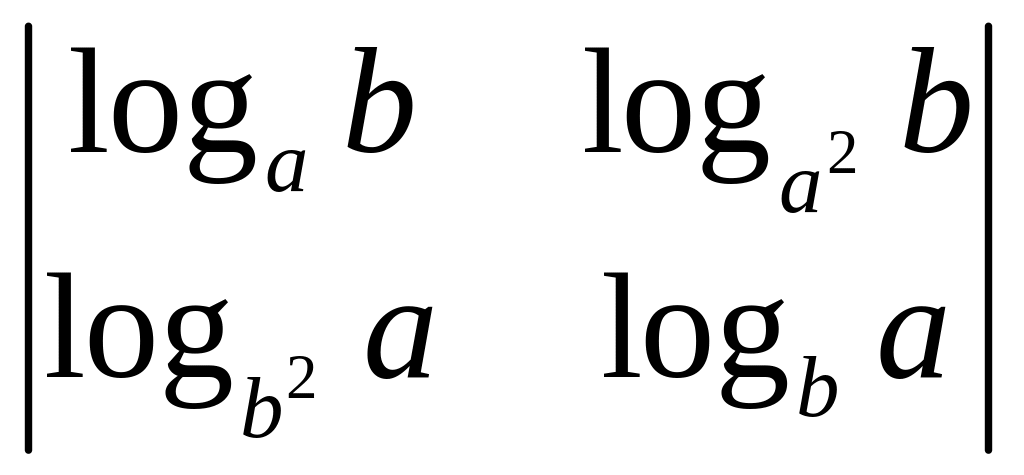 ;
4)
;
4)
![]() ;
5)
;
5)
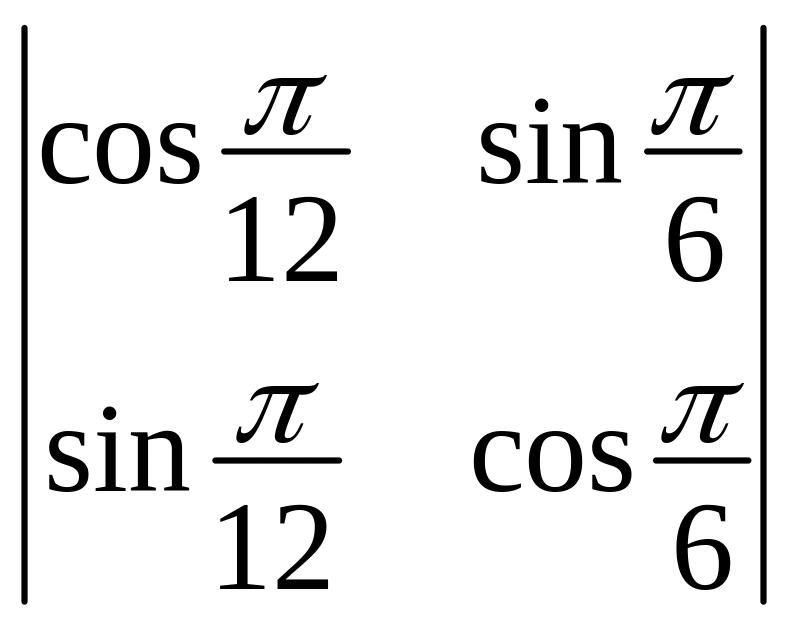 ;
;
6)
 ;
7)
;
7)
 ;
8)
;
8)
 ;
9)
;
9)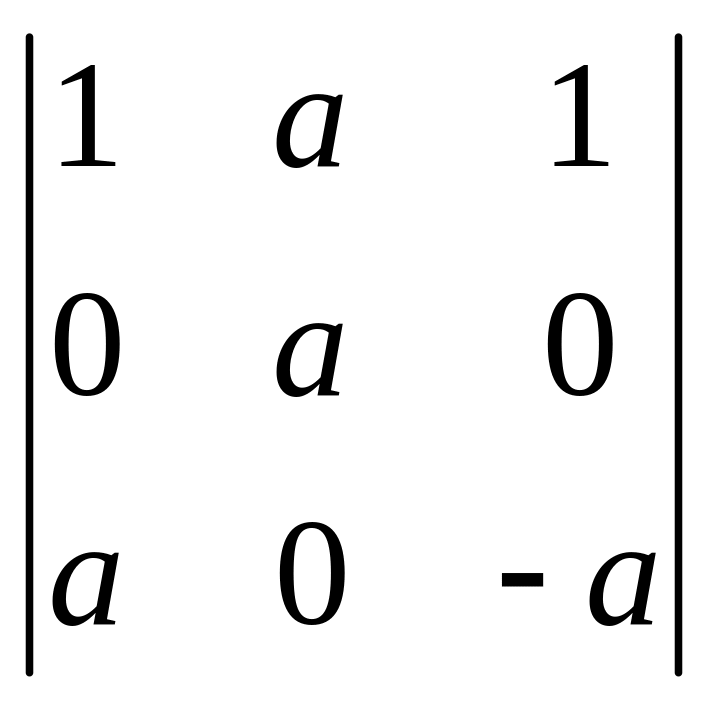 ; 10)
; 10)
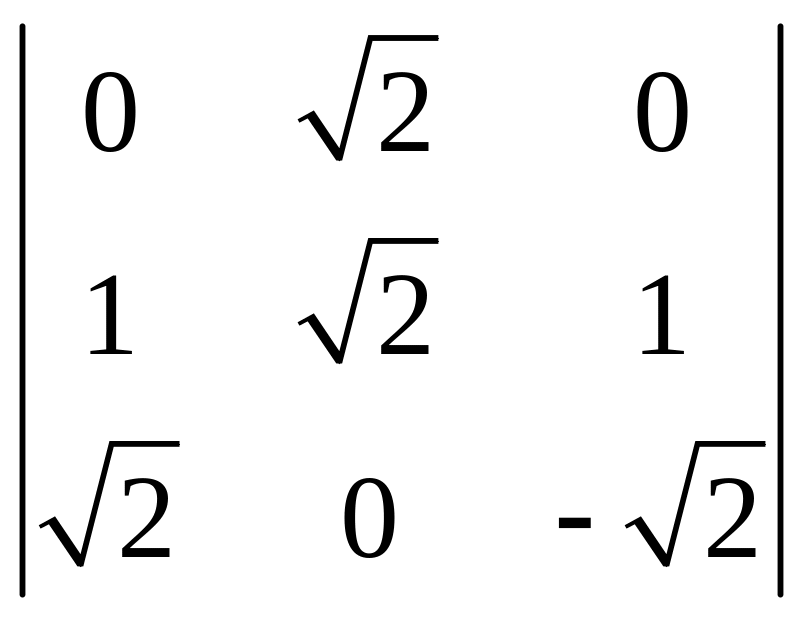 ;
;
11)
 ; 13)
; 13)
 ; 14)
; 14)
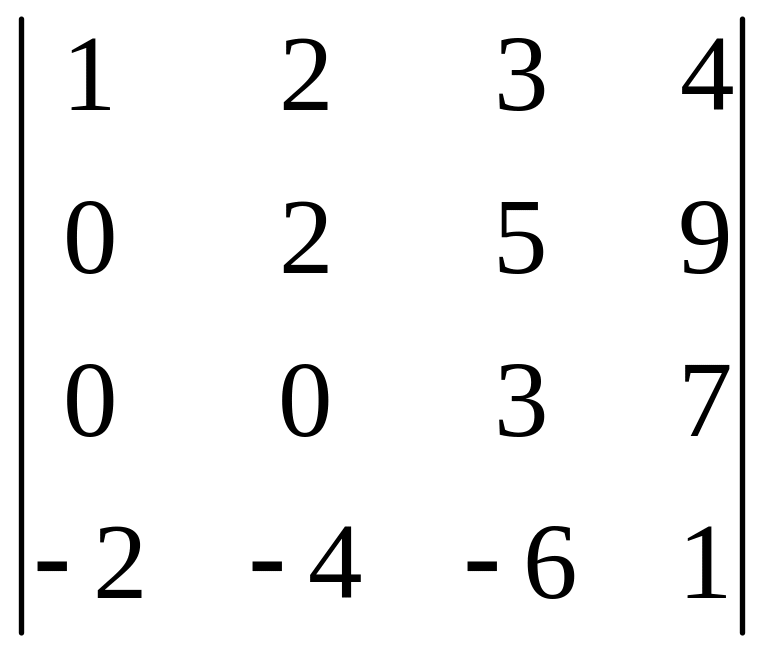 ;
;
Знайти обернену матрицю до матриць:
1)![]() ; 2)
; 2)![]() ; 3)
; 3)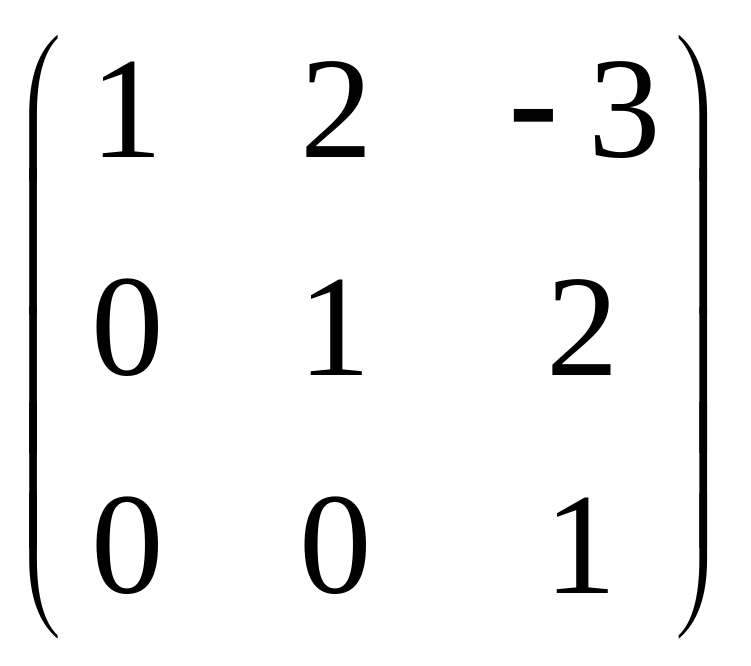 ; 4)
; 4)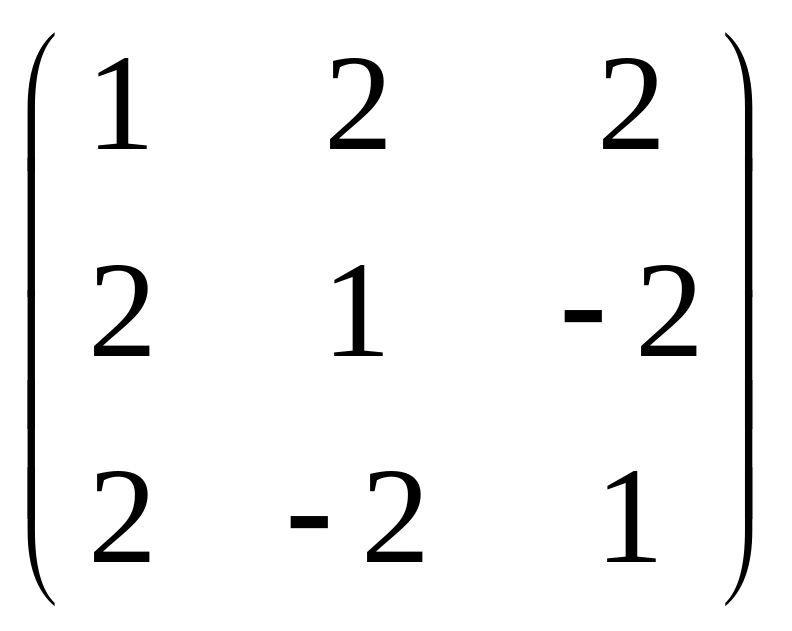 ; 5)
; 5)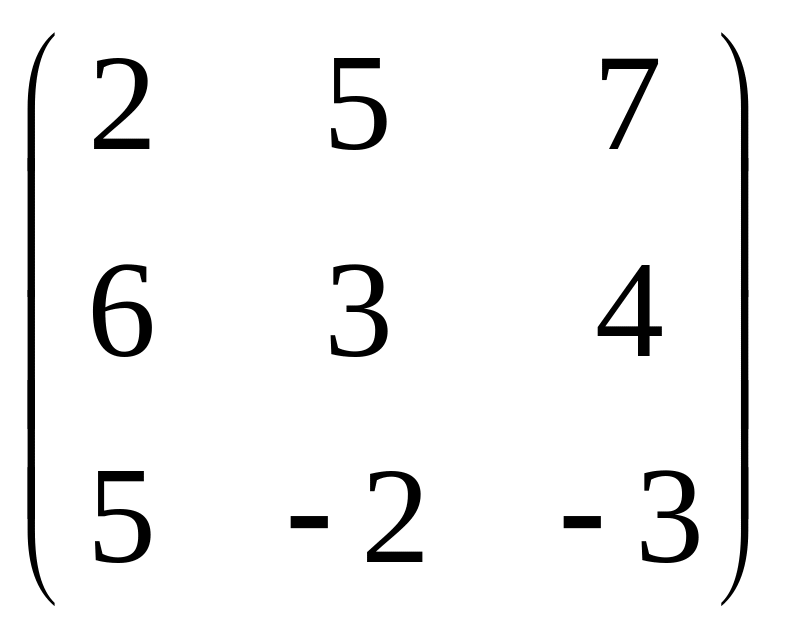 ;
6)
;
6)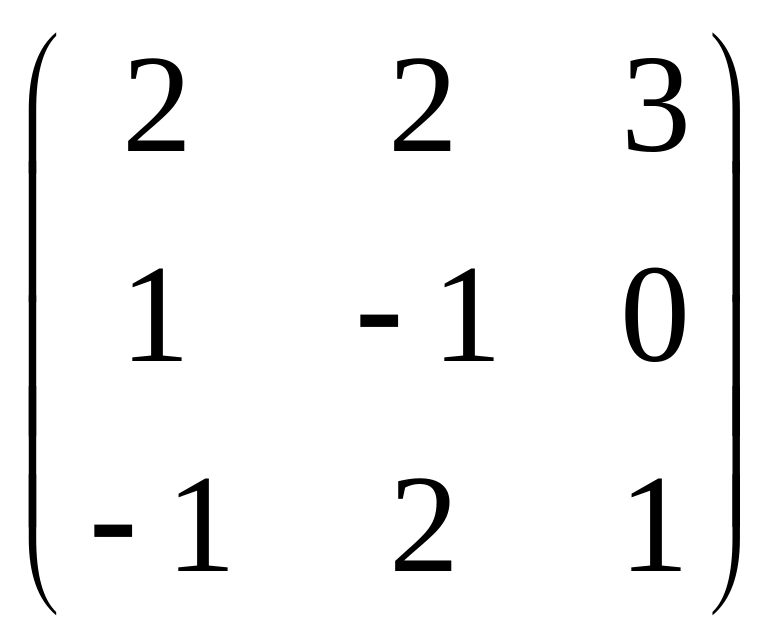 ;
;
7)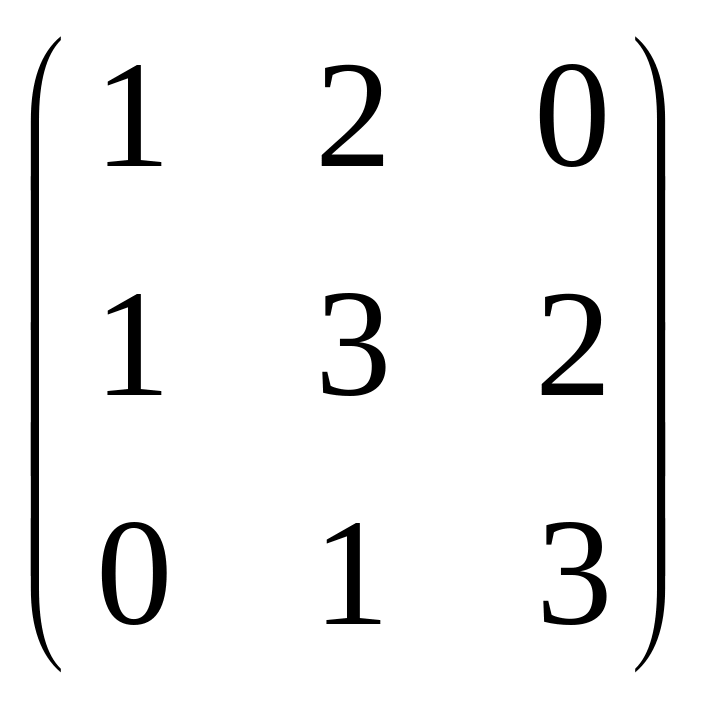 ; 8)
; 8)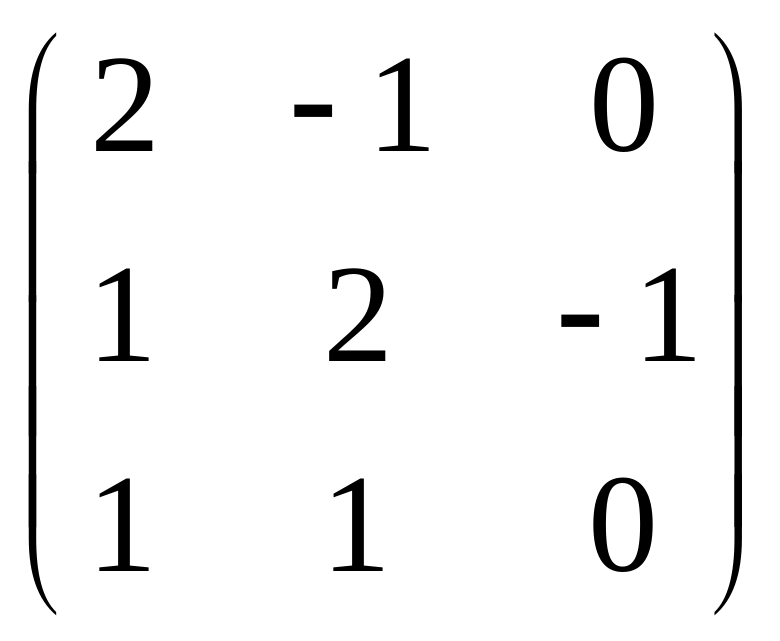 ; 9)
; 9)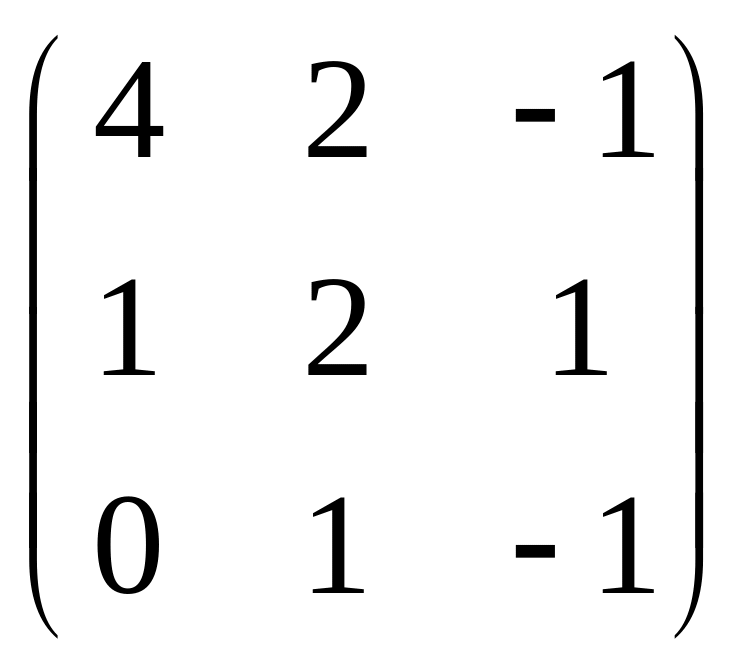 ;
10)
;
10)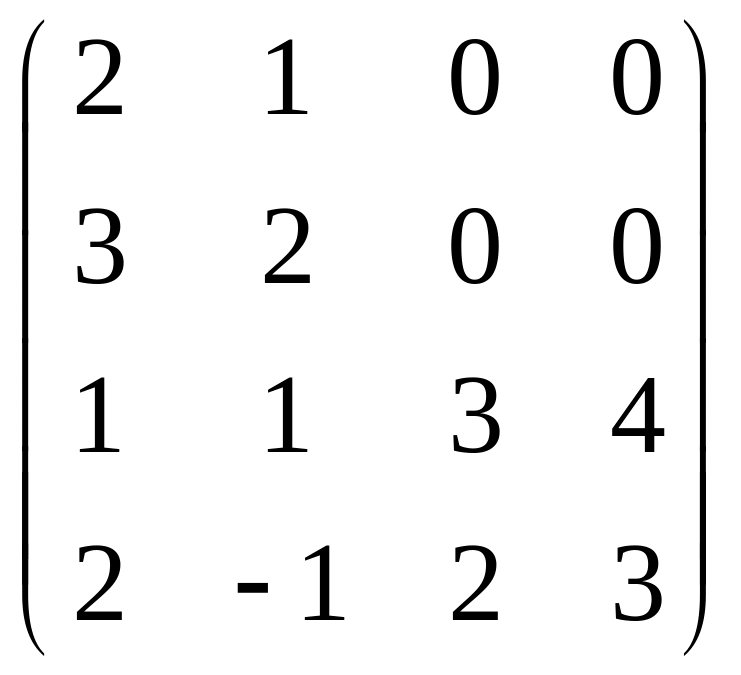 ;
11)
;
11)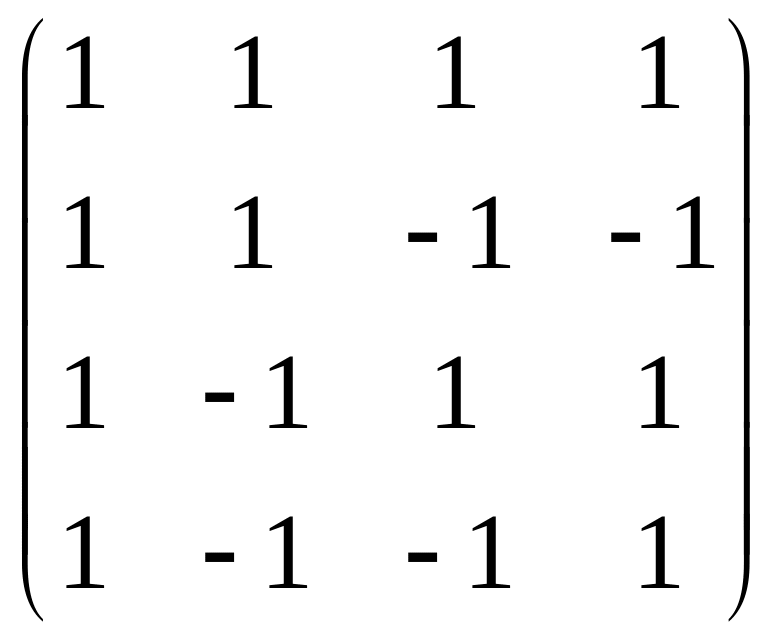 .
.
Знайти матрицю Х з рівняння:
1)![]() ; 2)
; 2)![]() ; 3)
; 3)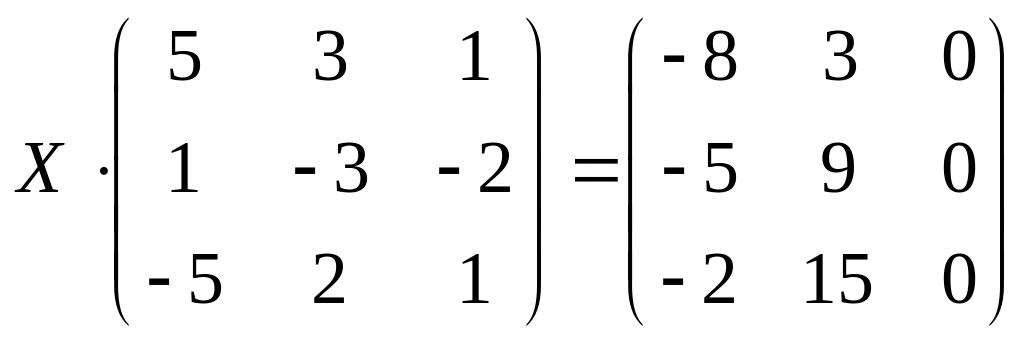 ;
;
4)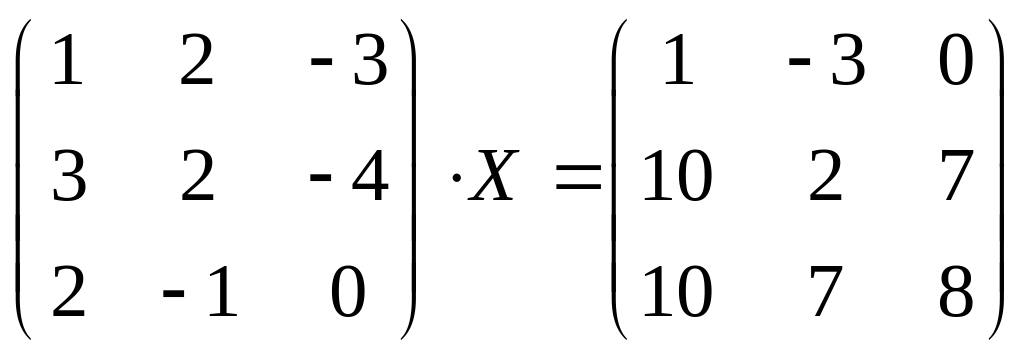 ; 5)
; 5)![]() ;
6)
;
6) .
.
Обчислити ранг матриці:
1)![]() ; 2)
; 2)![]() ; 3)
; 3) ; 4)
; 4)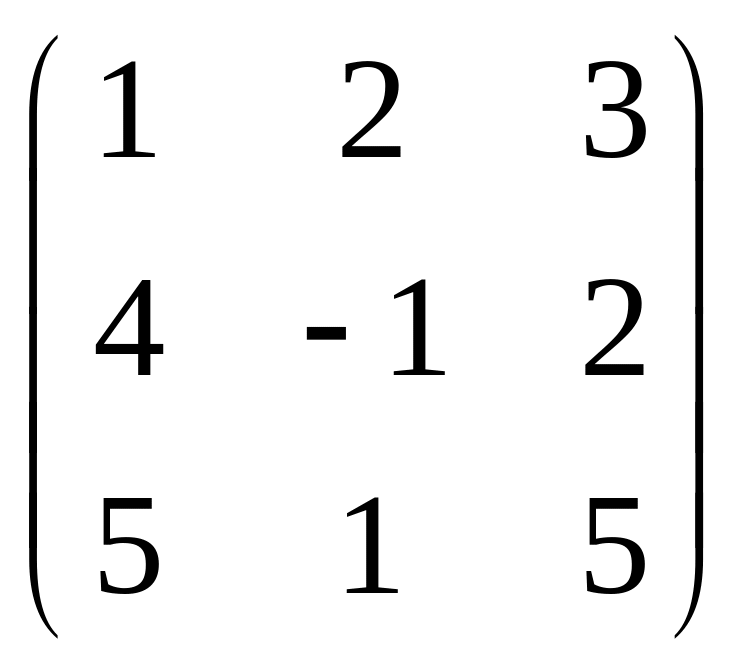 ; 5)
; 5)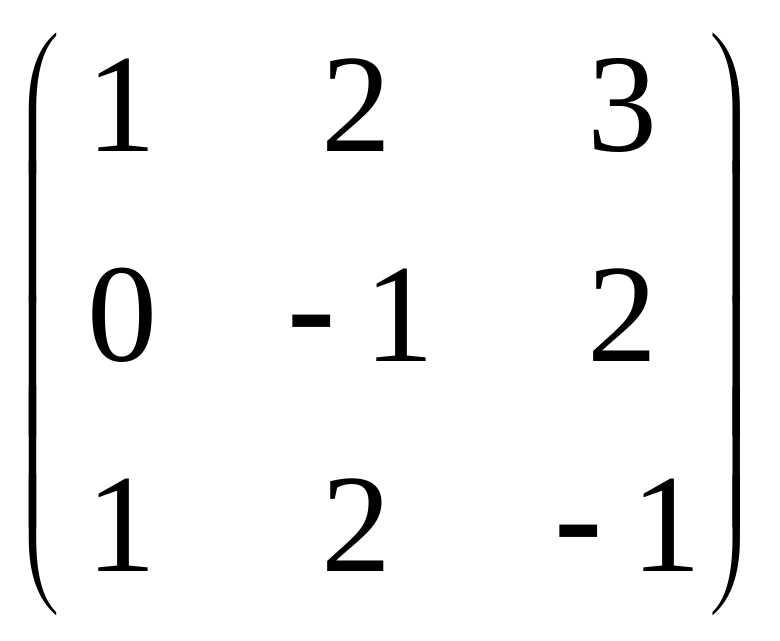 ;
;
Розв’язати системи рівнянь за правилом Крамера або подавши її у вигляді матричного рівняння.
1)![]() 2)
2)![]() 3)
3)
![]()
4)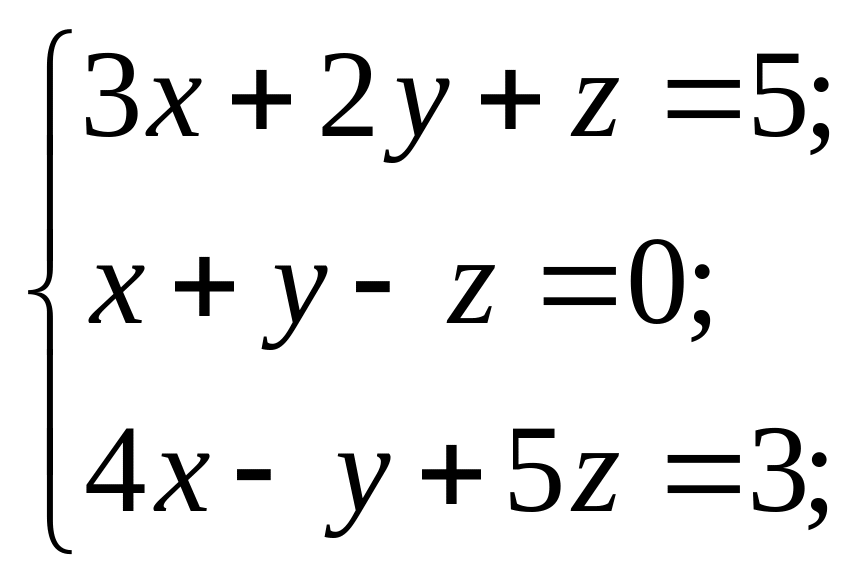 5)
5)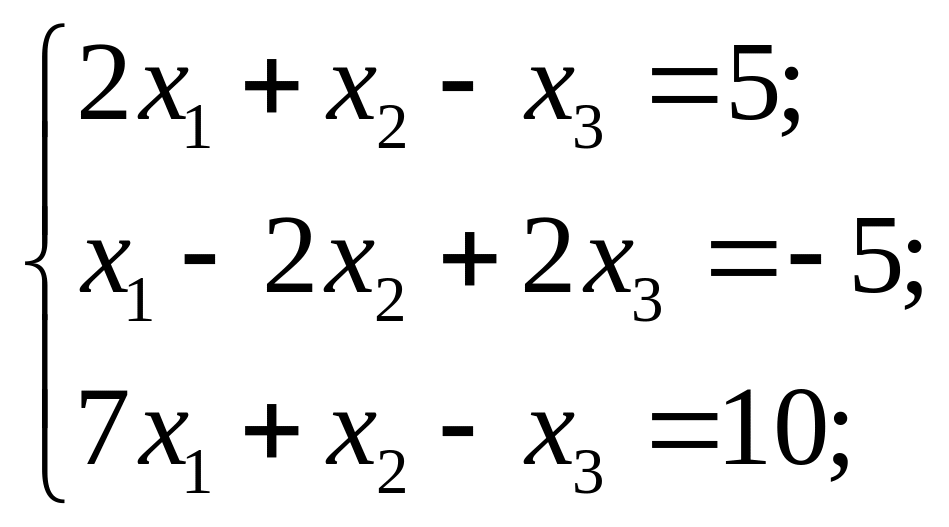 6)
6)
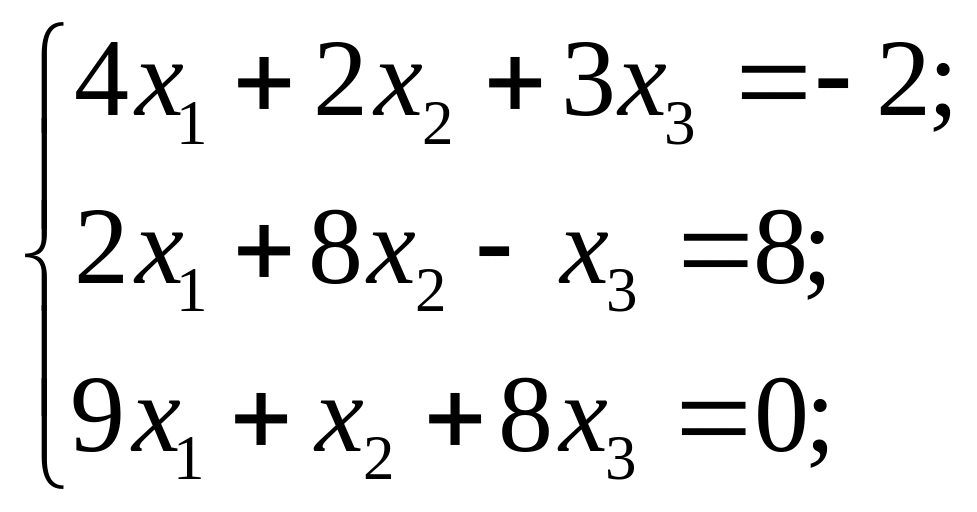
7)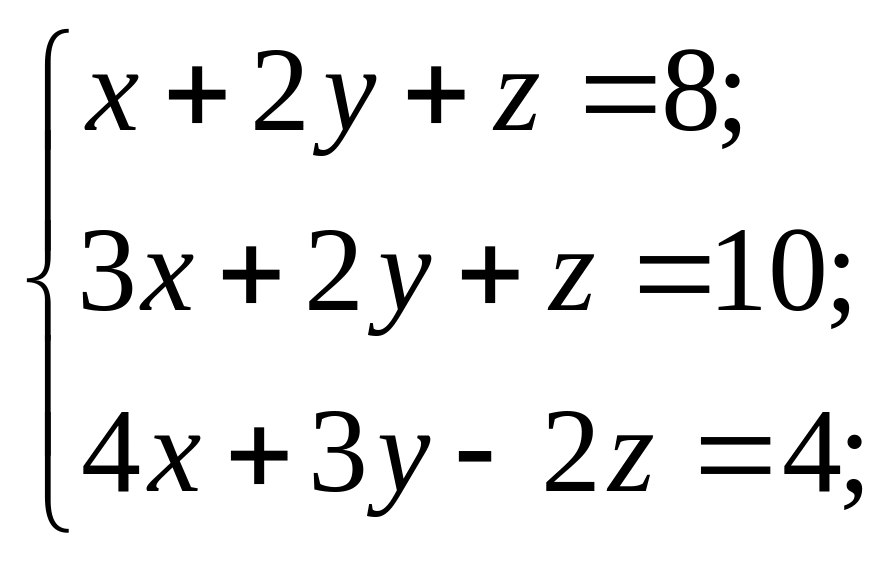 8)
8)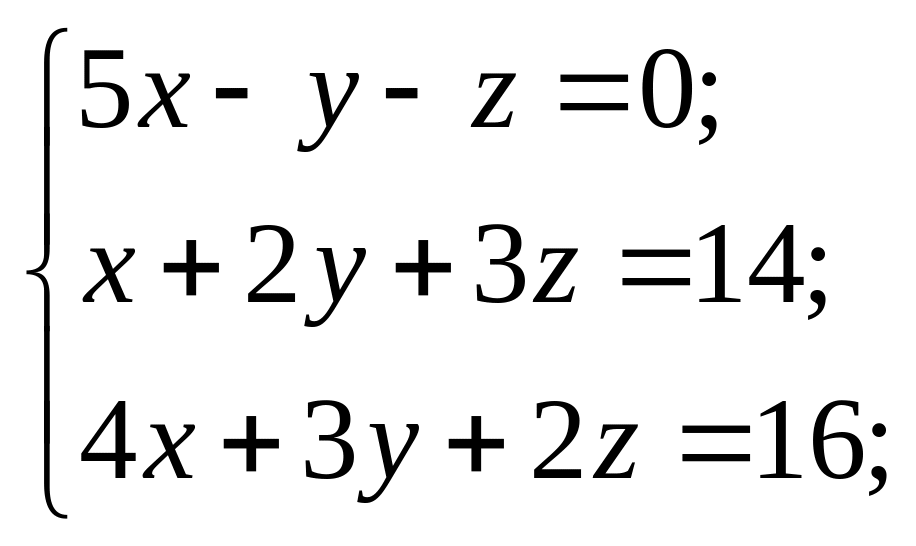 9)
9)
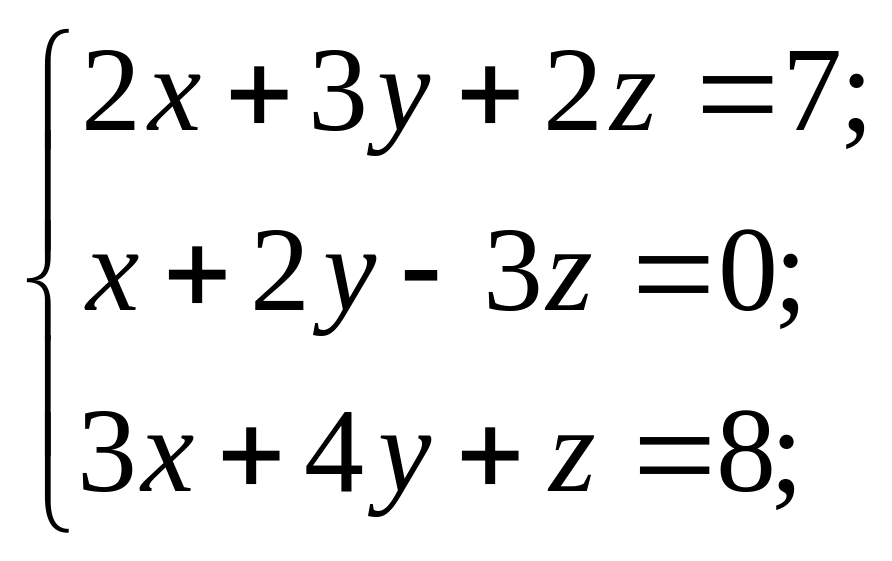
10) 11)
11)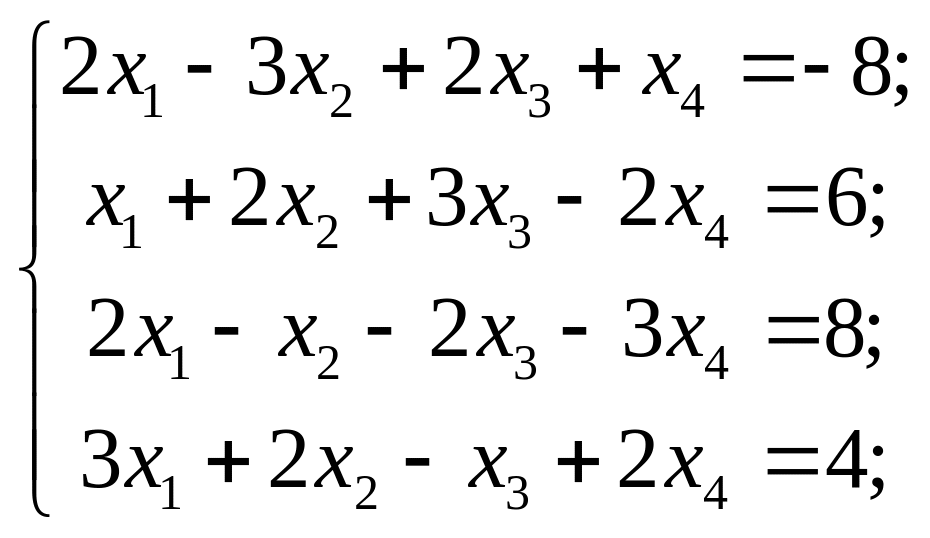 12)
12)

Матричним методом розв’язати системи рівнянь:
1) 2)
2)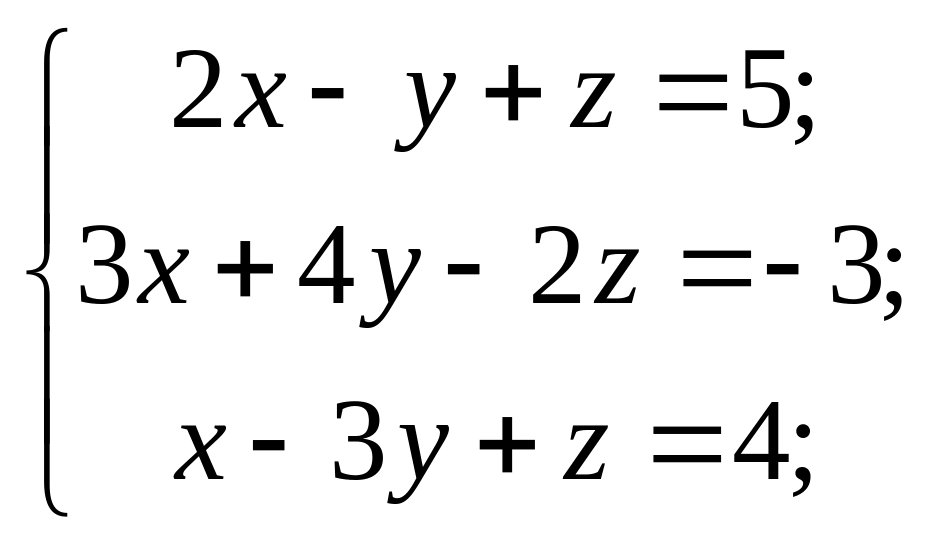 3)
3)
4) 5)
5)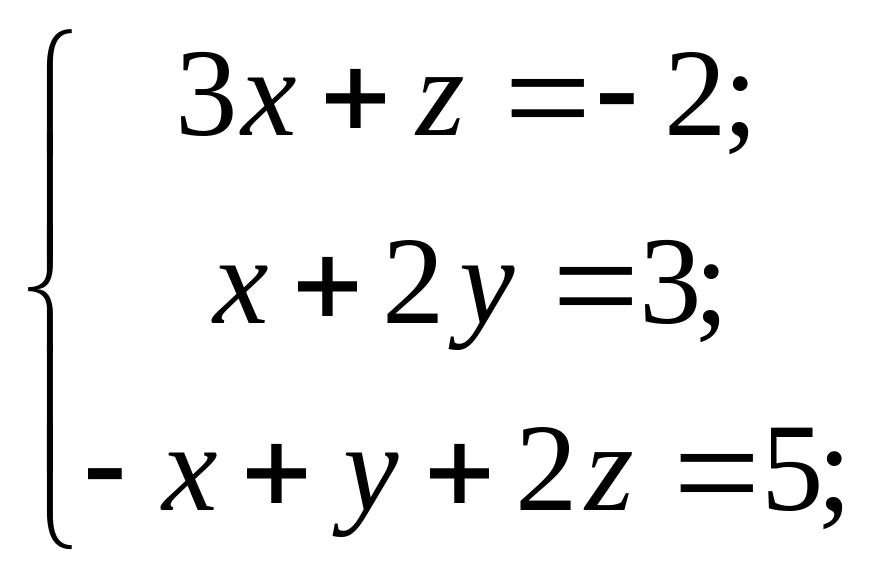 6)
6)
7)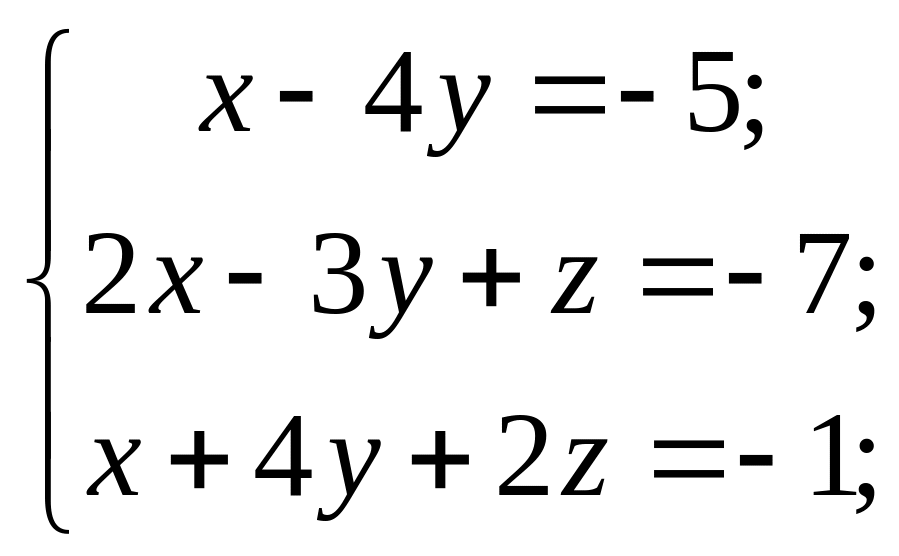 8)
8)
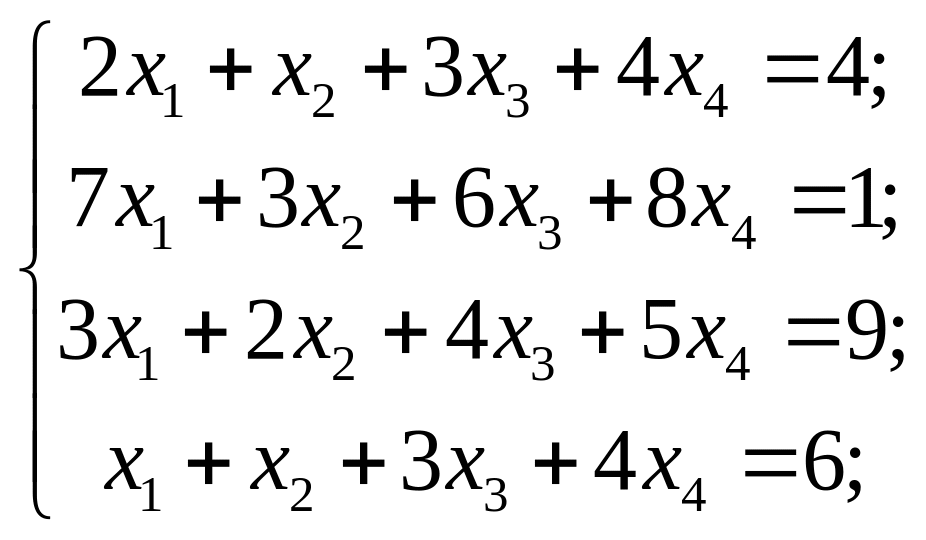
Розв’язати системи лінійних рівнянь методами Гаусса та Жордана-Гаусса
1)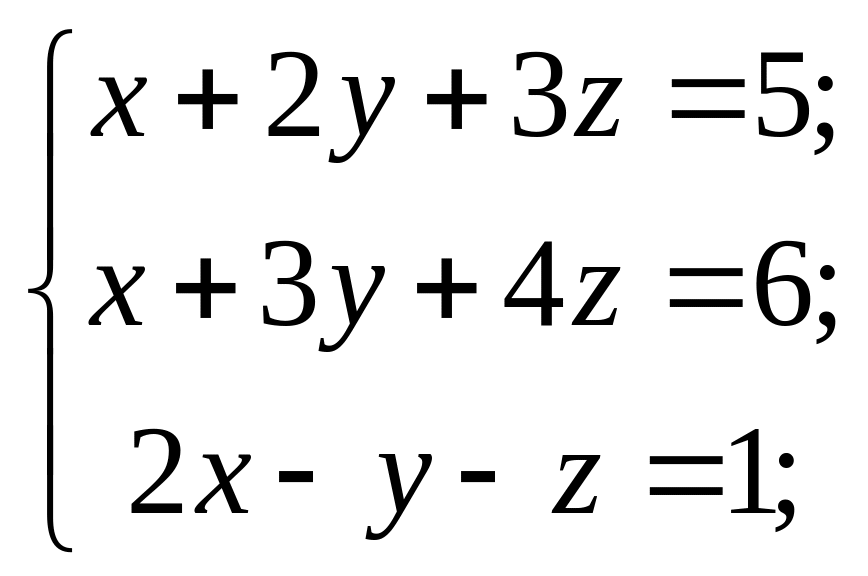 2)
2) 3)
3)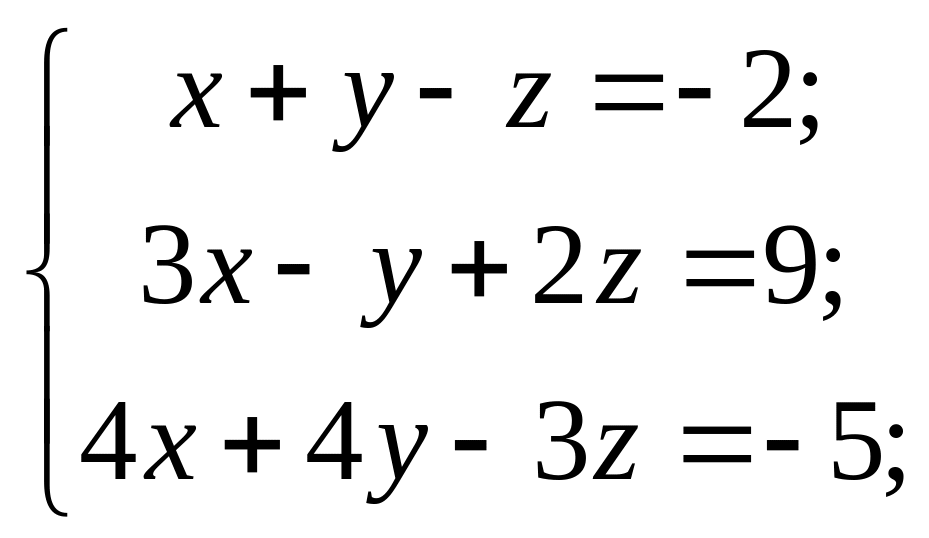
4)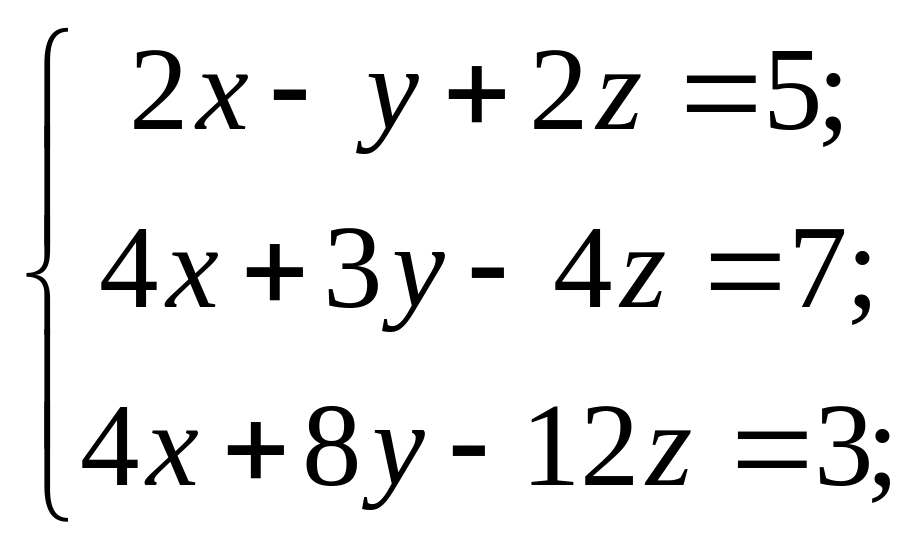 5)
5)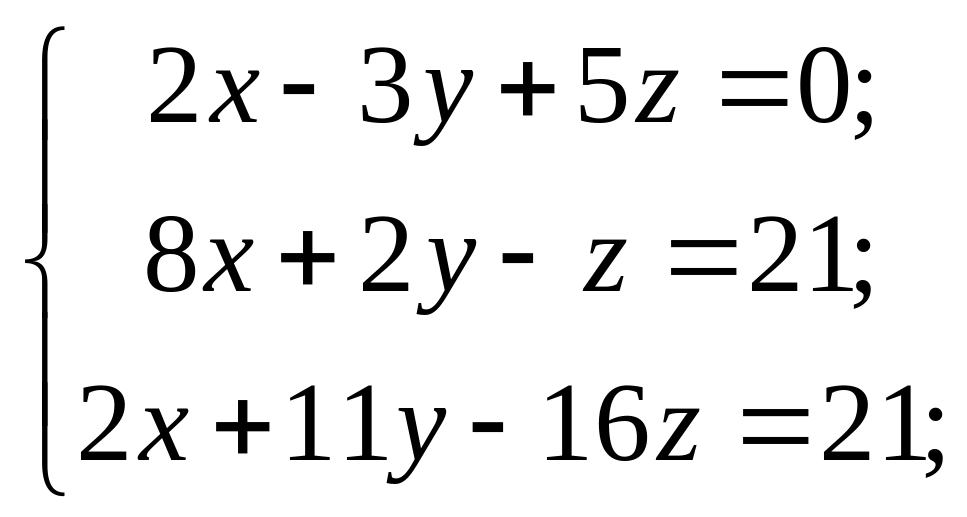 6)
6)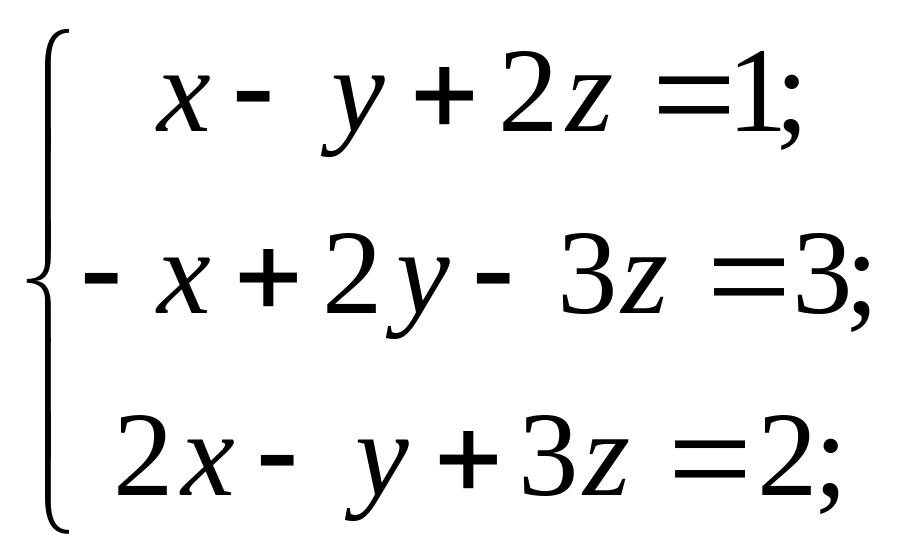
7) 8)
8)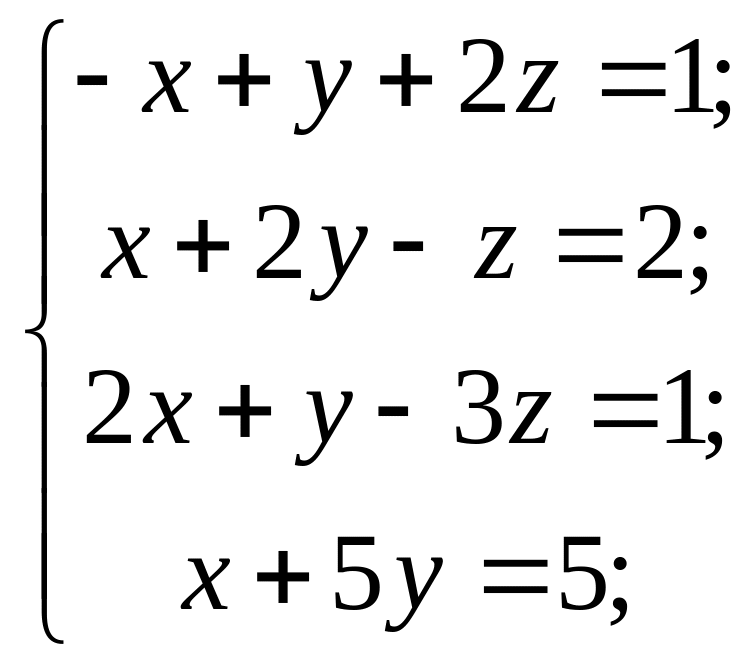 9)
9)
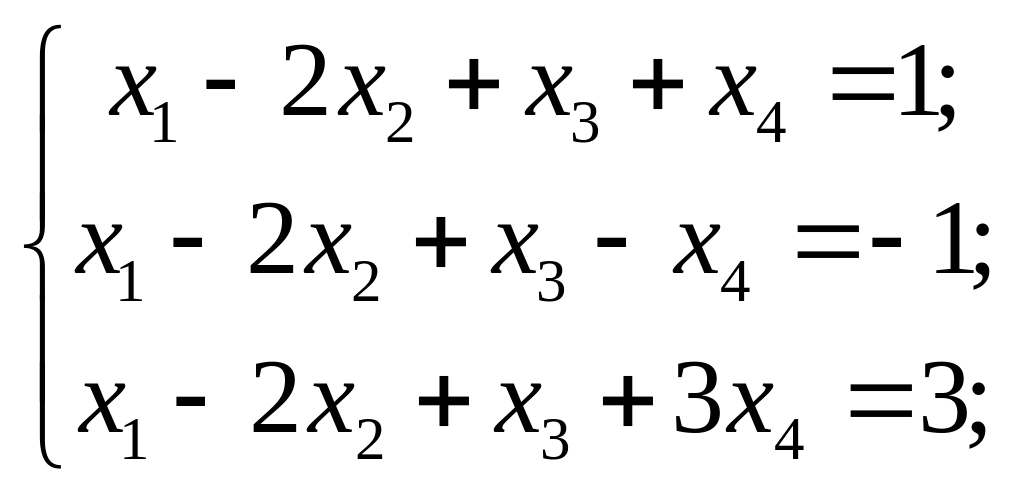
10)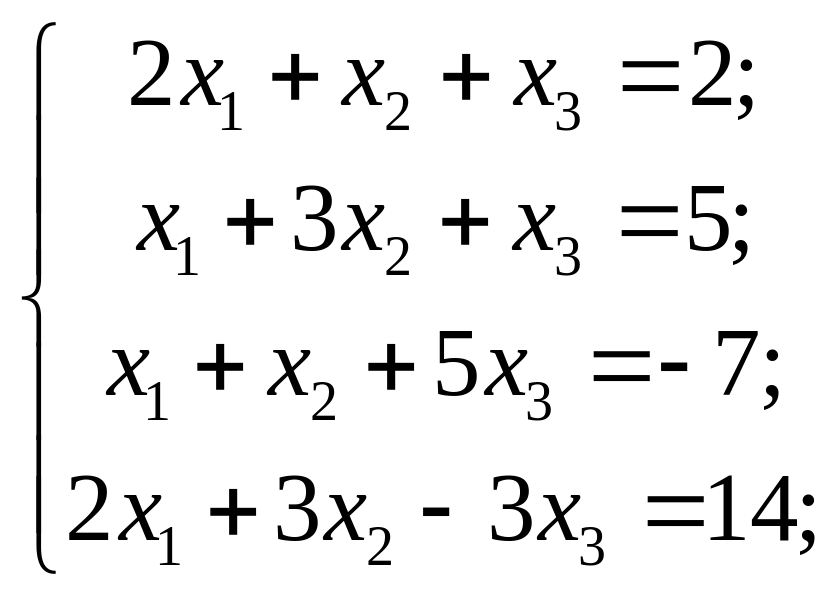 11)
11) 12)
12)
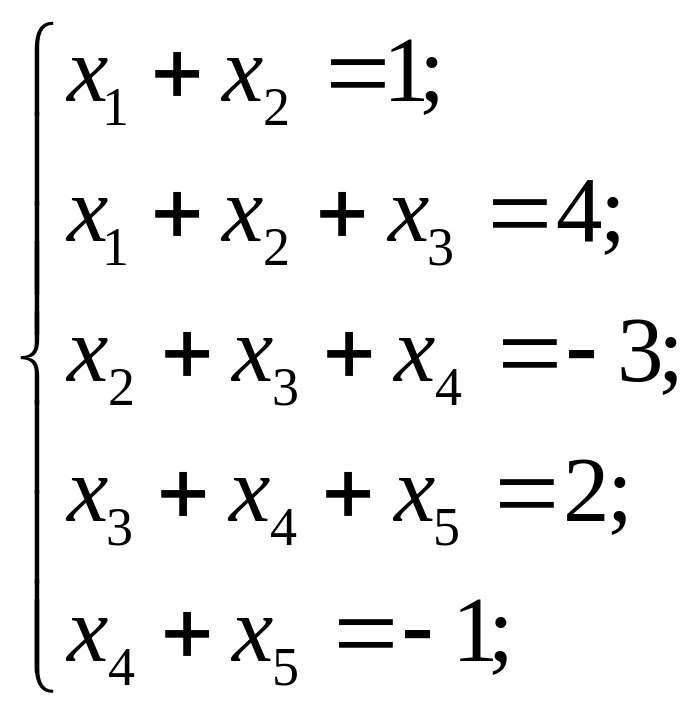
13)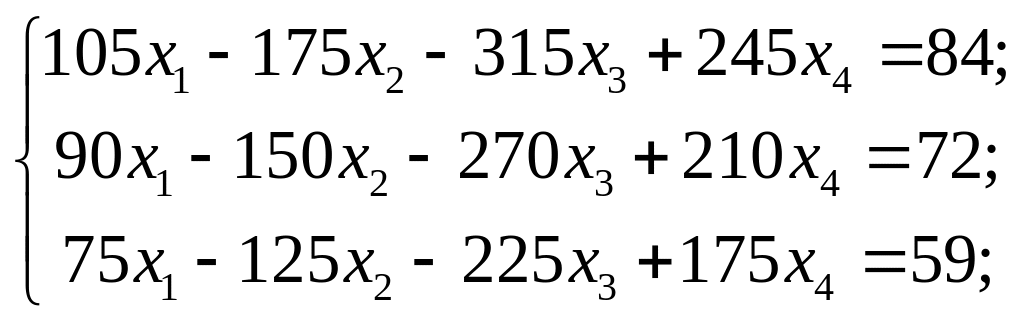 14)
14)
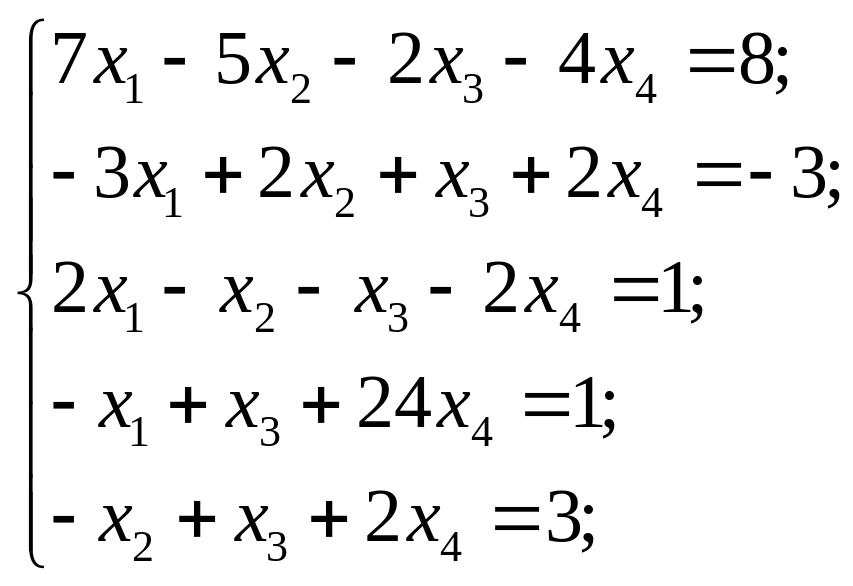
Дослідити на сумісність і знайти розв’язок систем:
1) 2)
2) 3)
3)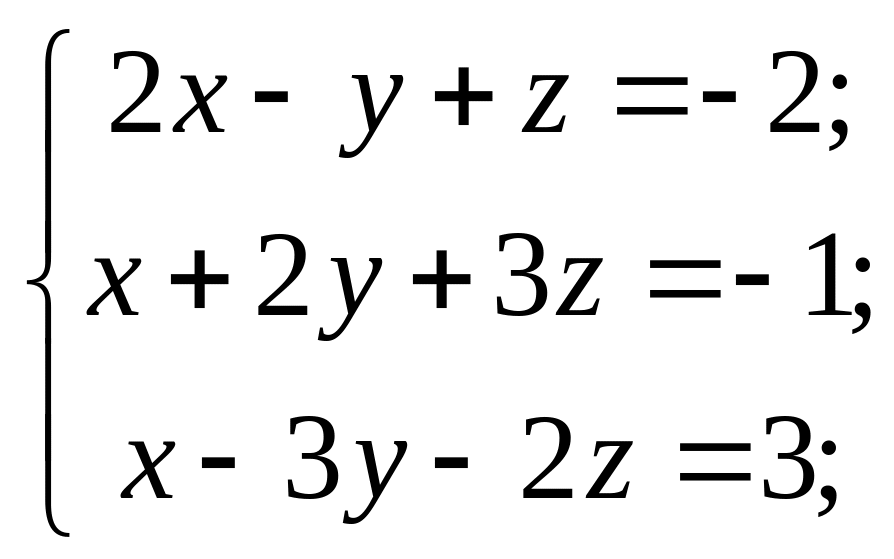 4)
4)

5)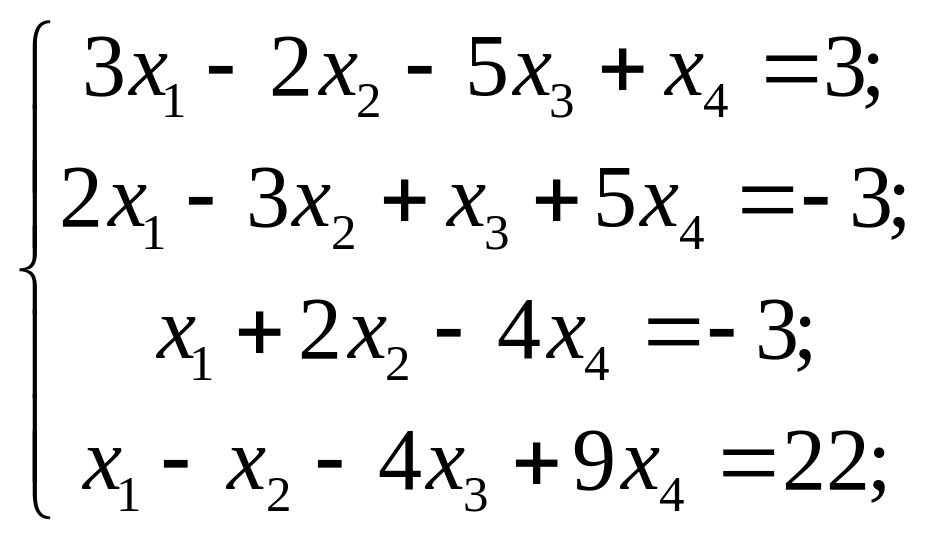 6)
6)
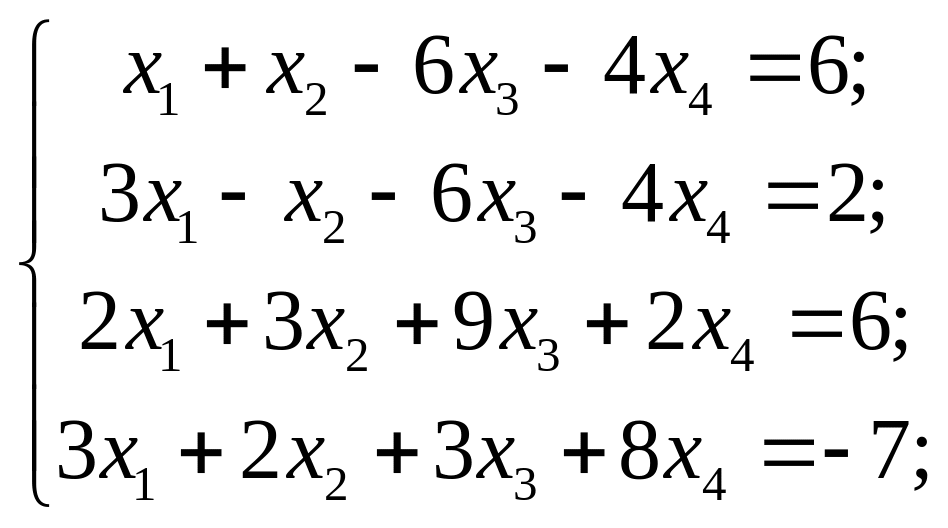 7)
7)
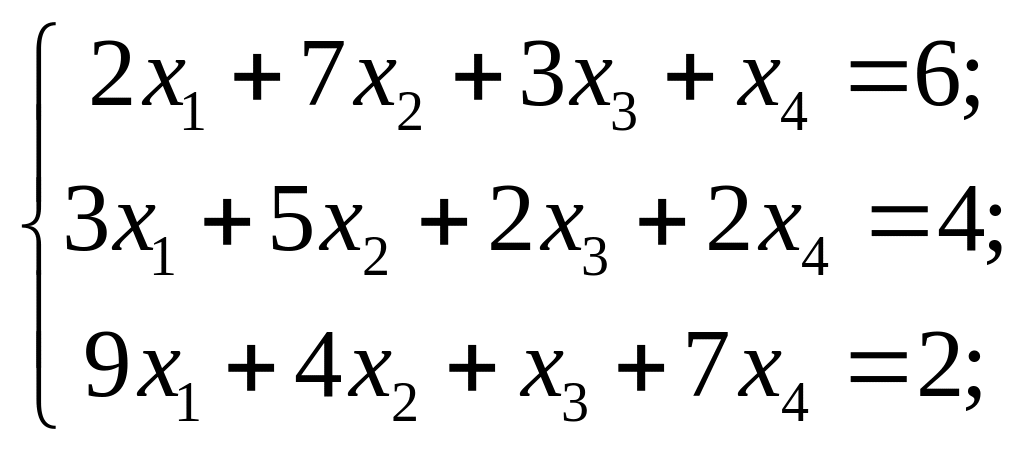
Змістовий модуль 2.
„Елементи векторної алгебри”
У трикутнику АВС вектор
 і вектор
і вектор
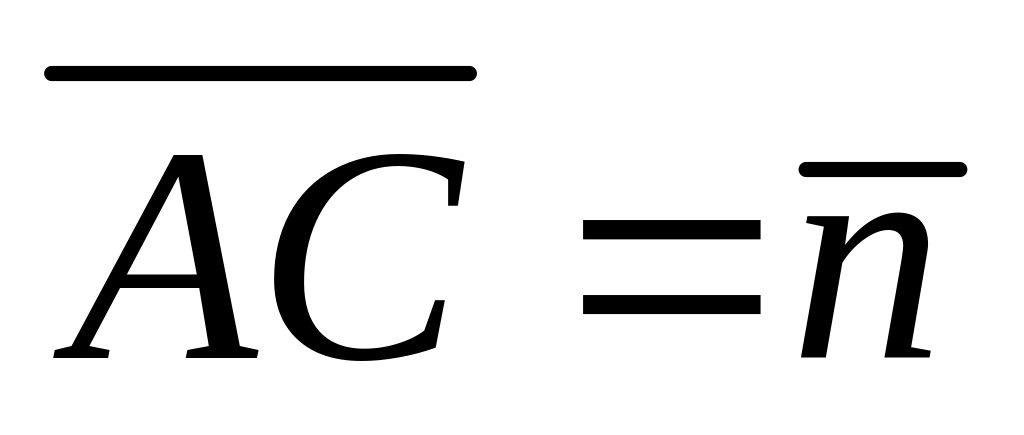 .
Побудувати вектори:
.
Побудувати вектори:
 ,
2)
,
2)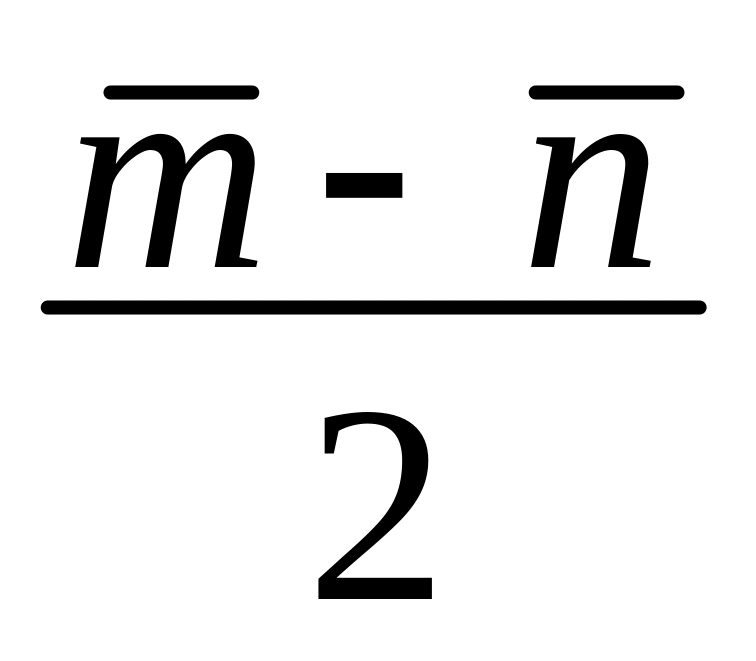 ,
3)
,
3)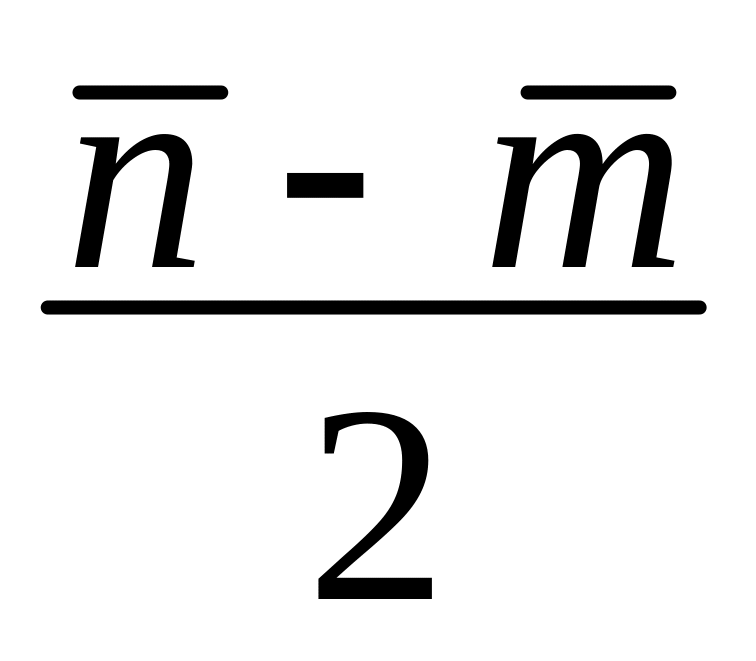 ,
4)
,
4)
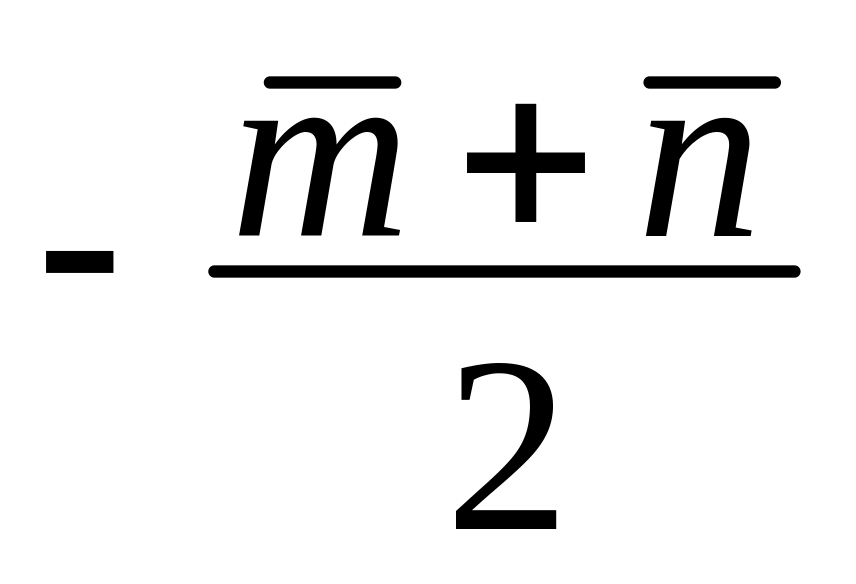 .
.
Задано вектори
 і
і
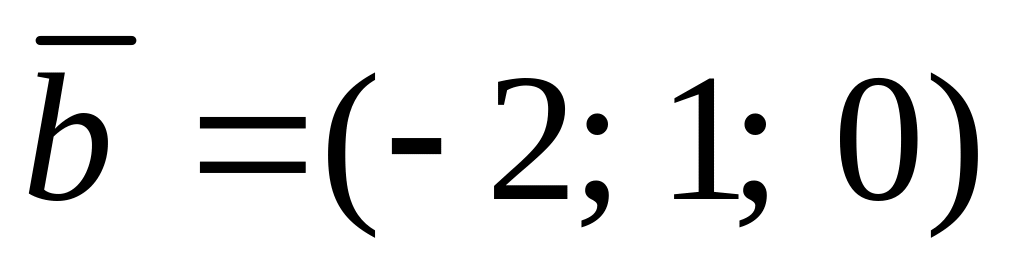 .
Визначити координати векторів :
.
Визначити координати векторів :
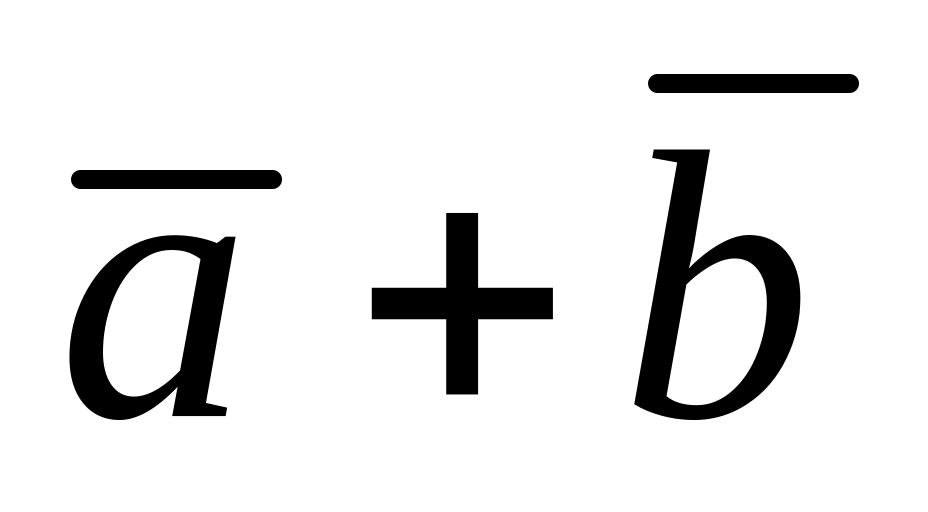 , 2)
, 2)
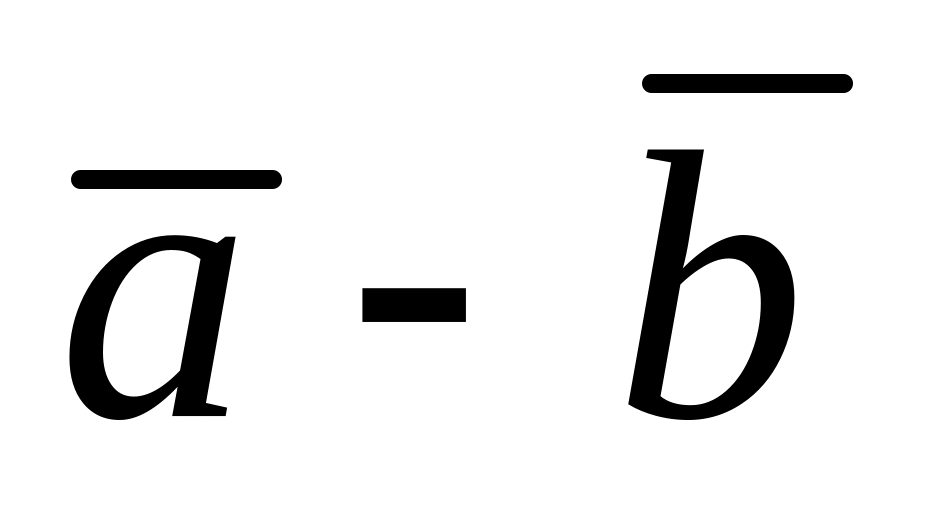 , 3)
, 3)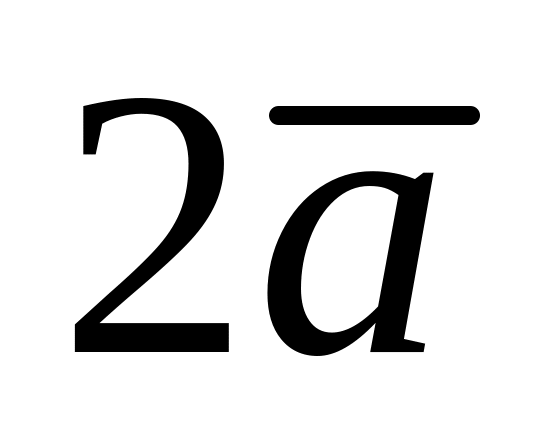 , 4)
, 4)
 , 5)
, 5)
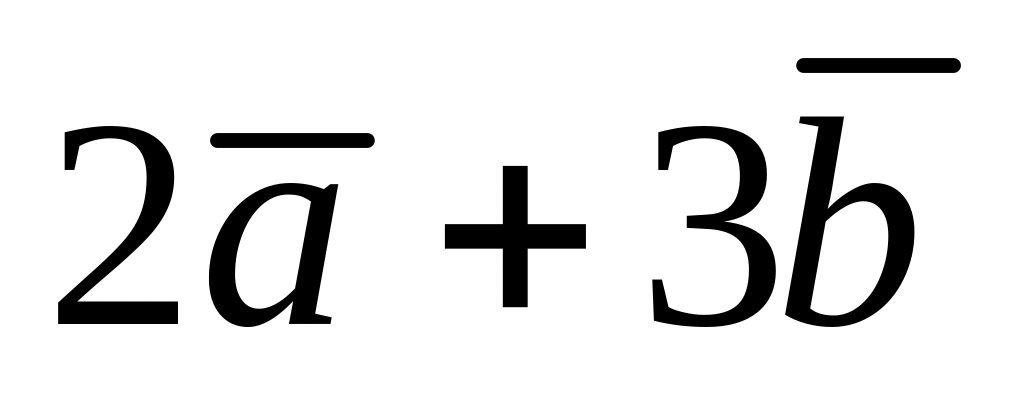 , 6)
, 6)
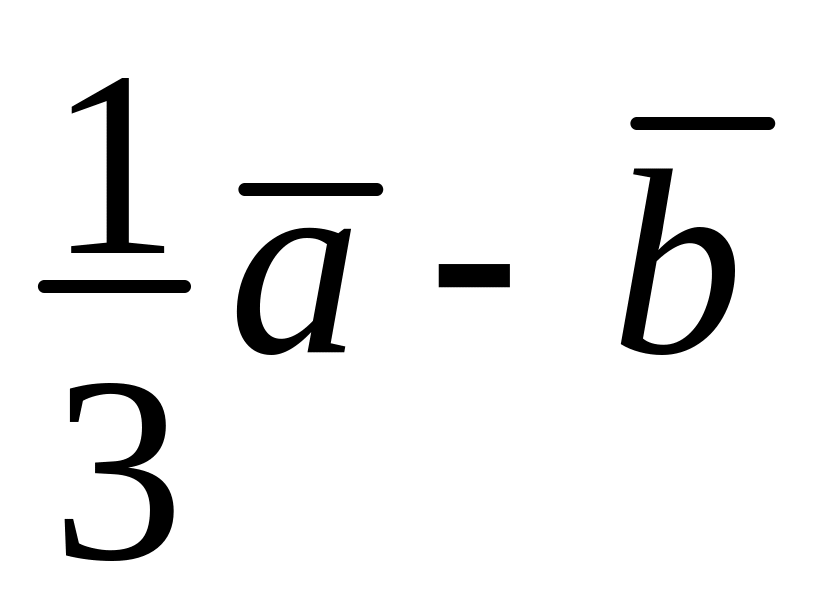 .
.
При яких значеннях α і β вектори
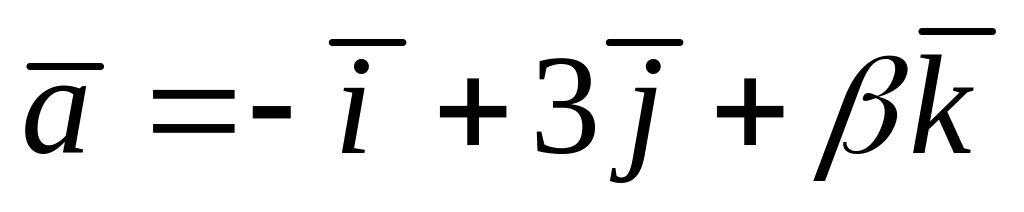 і
і
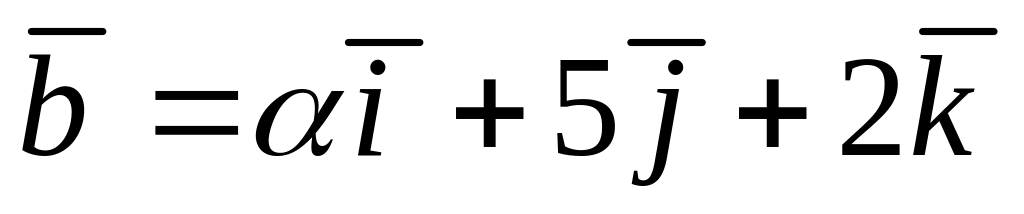 колінеарні?
колінеарні?Довести, що точки А(3; -1; 2), В(1; 2; -1), С(-1; 1; -3), D(3; -5; 3) є вершинами трапеції.
Дано вектори
 і
і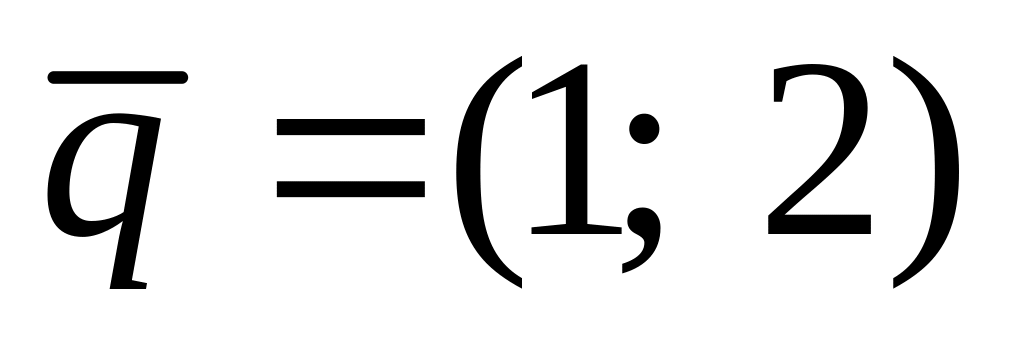 .
Розкласти вектор
.
Розкласти вектор
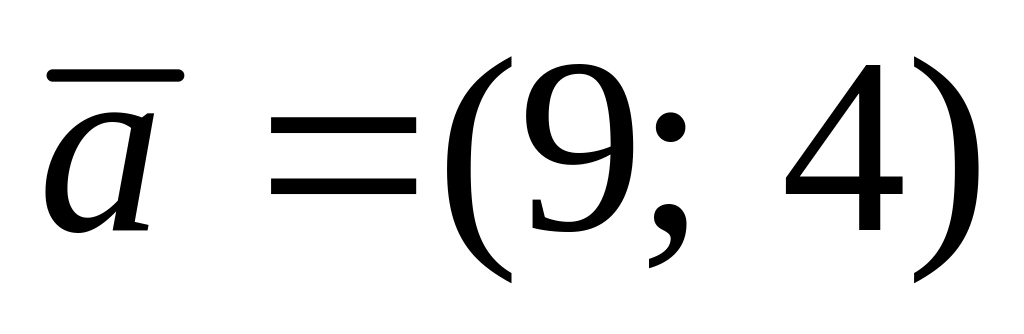 по базису
по базису
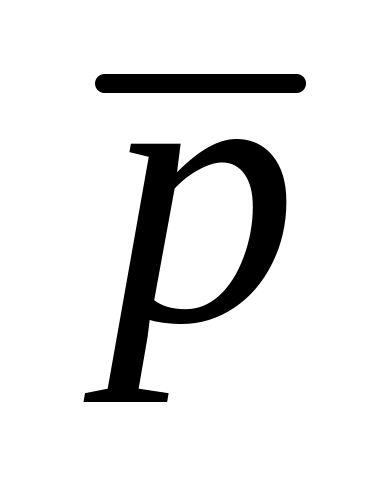 і
і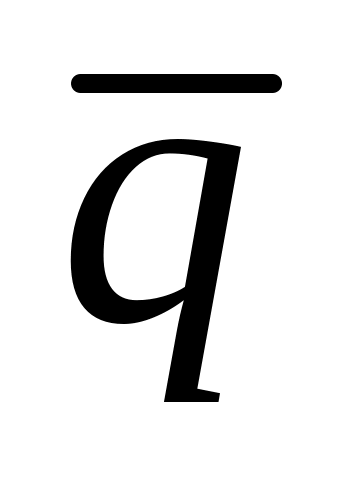 .
.Дано чотири вектори
 ,
,
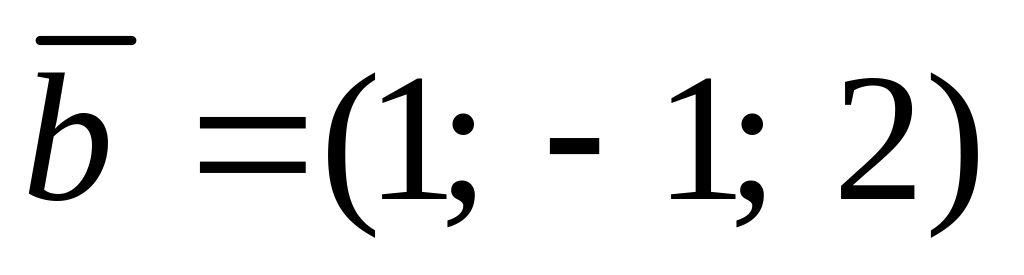 ,
,
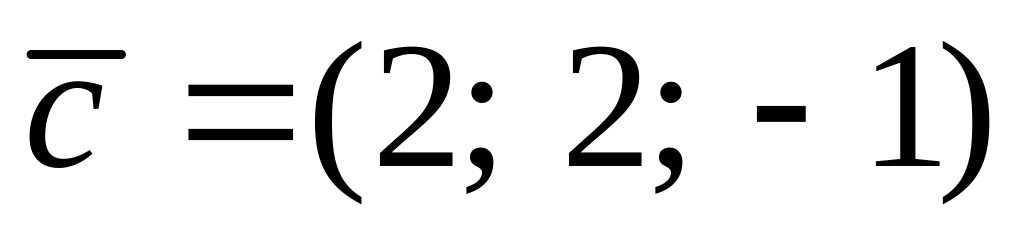 і
і .
Розкласти кожний з цих векторів,
приймаючи за базис три інші вектори.
.
Розкласти кожний з цих векторів,
приймаючи за базис три інші вектори.Дано точки
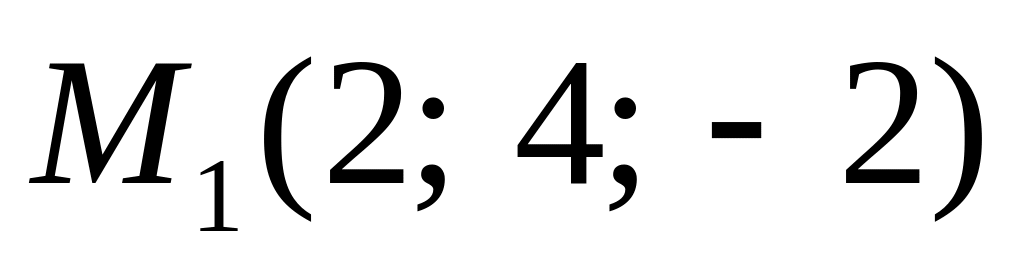 і
і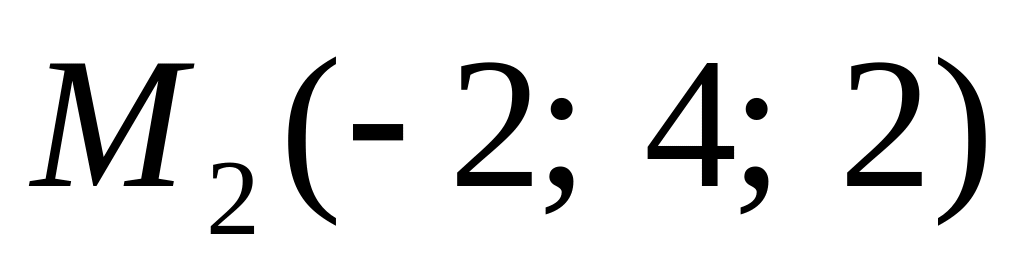 .
На прямій
.
На прямій
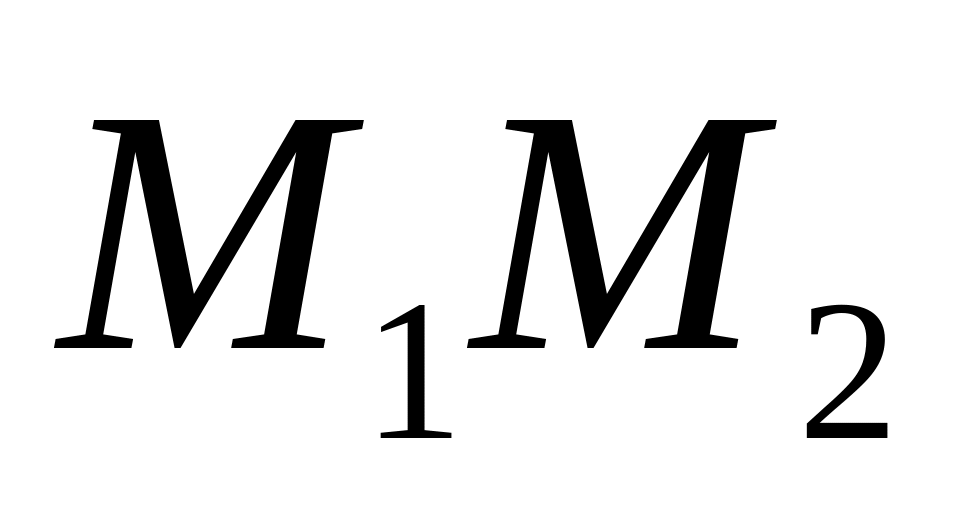 знайти точку M, яка ділить відрізок
у відношенні λ=3.
знайти точку M, яка ділить відрізок
у відношенні λ=3.Дано вершини трикутника: А(1; 1; 1), В(5; 1; -2), С(7; 9; 1). Знайти координати точки D перетину бісектриси кута А зі стороною СВ.
На осі Ox знайти точку, рівновіддалену від точок А(2; -4; 5) і В(-3; 2; 7).
В якому відношенні точка М, рівновіддалена від точок А(3; 1; 4) і В(-4; 5; 3), поділить відрізок осі Oy від початку координат до точки С(0; 6; 0).
Дано вершини чотирикутника А(1; -2; 2), В(1; 4; 0), С(-4; 1; 1), D(-5; -5; 3). Довести, що його діагоналі АС і BD взаємно перпендикулярні.
Обчислити внутрішні кути трикутника АВС, якщо
1) А(1; 2; 1), В(3; -1; 7), С(7; 4; -2); 2) А(2; -1; 3), В(1; 1; 1), С(0; 0; 5).
Дано точки А(-2; 3; -4), В(3; 2; 5), С(1; -1; 2), D(3; 2; -4). Обчислити проекцію вектора
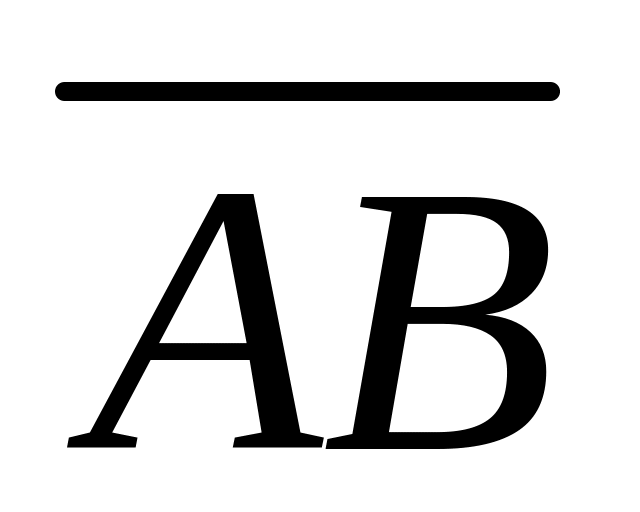 на вектор
на вектор .
.Обчислити площу трикутника з вершинами:
1) А(7; 3; 4), В(1; 0; 6), С(4; 5; -2); 2) А(1; 2; 0), В(3; 0; -3), С(5; 2; 6).
Дано вершини трикутника: А(1; -2; 8), В(0; 0; 4), С(6; 2; 0). Обчислити його площу і висоту ВD.
Обчислити об’єм піраміди з вершинами у точках A, B, C, D та довжину висоти, опущеної на грань АВС, якщо:
1) А(5; 2; 0), В(2; 5; 0), С(1; 2; 4) , D(0; 0; 0); 2) А(2; 0; 0), В(0; 3; 0), С(0; 0; 6) , D(2; 3; 8).
Довести, що точки A, B, C, D лежать в одній площині, якщо:
1) А(2; -1; -2), В(1; 2; 1), С(2; 3; 0) , D(5; 0; -6); 2) А(1; 2; -1), В(0; 1; 5), С(-1; 2; 1) , D(2; 1; 3).
Об’єм тетраедра V=5, три його вершини знаходяться у точках А(2; 1; -1), В(3; 0; 1), С(2; -1; 3). Знайти координати четвертої вершини D, якщо відомо, що вона лежить на осі Oy.
