7.14. Планарність графів.

Означення 7.38. Граф називається планарним (плоским), якщо існує ізоморфний йому граф, який може бути зображений на площині без перетину ребер (див. рис.7.23 а, б, в).

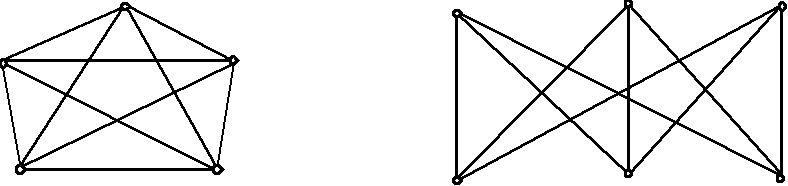
Розглядатимемо повні графи. Очевидно, повні графи на двох вершинах (рис.7.23 а), так і на трьох (рис.7.23 б) та чотирьох (рис.7.23 в) вершинах також є плоским. Повний граф на п’яти вершинах (рис.7.23 г) не є планарним, а граф − це повний плоский граф із максимальною кількістю вершин.

а)	б)		в)
г)		д)
Рис.7.18

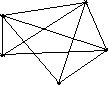
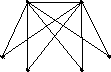
Розглянемо повний дводольний граф (рис.7.18 б), який є математичною моделлю відомої задачі про три будинки і три колодязі, що формулюється так. Є три будинки і три колодязі. Сусіди ворогують, не хочуть зустрічатися, але хочуть користуватися всіма трьома колодязями. Чи можна прокласти стежки від кожного будинку до кожного колодязя так, щоб вони не перетиналися? Ця задача нерозв’язна, тому що граф − неплоский.

Графи і відіграють фундаментальну роль у теорії планарності. Їх називають графами Понтрягіна-Куратовського.

Справджується таке твердження.

Граф є планарним (плоским) тоді і тільки тоді, коли він не містить підграфів Понтрягіна-Куратовського.

Позначимо -й ступінь матриці суміжності орграфа (аналогічно для графа ).

Вправа 7.3.

Зображено графи (рис.7.19)

а)	б)	в)
Рис.7.19

1) Визначити максимальний підграф, який є деревом.

2) Навести приклади маршрутів, ланцюгів, циклів, простих ланцюгів, простих циклів.

3) Визначити максимальний підграф кожного графа, який є ейлеревим.

4) Визначити максимальний підграф кожного графа, який є гамільтоновим.

5) Визначити максимальний планарний підграф.

6) Визначити цикломатичні числа кожного графа.

7.15. Задачі пошуку маршрутів в графі.

При розв’язанні широкого кола прикладних задач нерідко виникає необхідність знайти маршрут, що зв’язує задані вершини в графі . Наведемо алгоритм розв’язання її у загальному вигляді:

Алгоритм Террі. Задача зводиться до пошуку маршруту у зв’язному графі , який з’єднує задані вершини , де .

Нехай − зв’язний граф. Треба знайти маршрут, що зв’язує задані вершини , де , у графі . У зв’язному графі завжди можна знайти маршрут, що зв’язує дві задані вершини та , якщо, виходячи з вершини і здійснюючи послідовний перехід від кожної досягнутої вершини до суміжної з нею, керуватися такими правилами:

1) йдучи по довільному ребру, кожний раз відмічати напрямок, в якому воно було пройдене;

2) виходячи з деякої вершини , завжди рухатися тільки по тому ребру, яке не було пройдене або було пройдене у зворотному напрямку;

3) для кожної вершини , відмінної від , відмічати те ребро, яке першим заходить у , якщо вершина зустрічається вперше;

4) виходячи з деякої вершини , відмінної від , по першому ребру, яке заходить у , рухатися лише тоді, коли немає інших можливостей.

Приклад 7.19. Використовуючи алгоритм Террі, знайти маршрут, що зв’язує і у графі , зображеному на рис.7.20 а. Граф − це схема лабіринту, де − вихід із нього, а − розвилка, з якої починається пошук виходу.

а)	б)
Рис.7.20

Пошук вершини у будемо здійснювати так, неначе нічого невідомо про цей граф. На рис.7.20 б) показано один із можливих варіантів руху по графу згідно з алгоритмом Террі. Пронумерованими штриховими дугами зображено схему руху по графу . Знаками помічено перші ребра, які заходять у вершини (помітка робиться ближче до тієї вершини, в яку ребро заходить). Ця схема руху відповідає маршруту . Зазначимо, що після того, як із вершини зайшли у вершину , внаслідок правила 4 не можна повернутися у , оскільки існують інші можливості, а є першим ребром, що заходить у . Далі, після того, як із вершини зайшли у вершину , внаслідок правила 4 треба рухатися знов до вершини , і далі в наслідок правила 2 рухатися до вершини .