7.3. Подання графа за допомогою матриці суміжності графа.

Матриця суміжності графа - це квадратна матриця , стовпцям і рядкам якої відповідають вершини графа. Для неорієнтованого графа дорівнює кількості ребер, інцидентних -й і -й вершинам, для орієнтованого графа цей елемент матриці суміжності відповідає кількості ребер з початком у -й вершині й кінцем у -й. Таким чином, матриця суміжності неорієнтованого графа симетрична (), а орієнтованого – необов'язково.

Приклад 7.4. Задамо матрицю суміжності графа, що наведений на рис.7.3 (табл.7.3) і графа, що наведений на рис. 7.2. в (табл.7.4).

Таблиця 7.3.							Таблиця 7.4.
	0	1	1	1	0			0	3	0
	1	0	1	0	0			0	0	1
	1	1	0	1	1			0	1	1
	1	0	1	0	1
	0	0	1	1	0

Матриця суміжності повністю визначає відповідний неорієнтований або орієнтований граф. Число його вершин дорівнює розмірності матриці , -й і -й вершинам графа інцидентні ребер. Для неорієнтованого графа , і всі його ребра визначаються верхнім правим трикутником матриці, розташованим над діагоналлю, включаючи останню. Кількість ребер графа дорівнює сумі у цьому трикутнику, тобто . Ребра орієнтованого графа визначаються всіма елементами матриці суміжності.

7.4. Визначення локальних степенів вершин графа. Повні графи.

Якщо задані матриці суміжності або інцидентності графа, можна визначити локальні степені всіх його вершин. Дійсно, в -му стовпці матриці інцидентності, який відповідає вершині , одиниці знаходяться на перетині з рядками, яким відповідають інцидентні цій вершині ребра, а інші елементи стовпця дорівнюють 0. Отже,

.

Елементи ж матриці суміжності – це кількості ребер, інцидентних вершинам і . Звідси .

Для вершин орієнтованого графа визначаються два локальних степеня: – число ребер з початком у вершині , або, інакше, кількість ребер, які виходять з , і – кількість ребер, що входять у ребра , тобто ребер, для яких ця вершина є кінцем. Петля дає внесок 1 у обидва ці степені. Локальні степені вершин орієнтованого графа визначаються через коефіцієнти його матриці суміжності: . Вираз їх через коефіцієнти матриці інцидентності – значно складніше.

Оскільки кожне ребро орієнтованого графа має один початок й один кінець, суми та дорівнюють кількості ребер цього графа, а отже, є рівними між собою:

.

Приклад 7.5. Для графа, що заданий на рис.7.3, визначимо локальні ступені його вершин за матрицею інцидентності (табл.7.1), підраховуючи суми одиниць в стовпцях.

, , , , .

Для того ж самого графа, що заданий на рис.7.3, визначимо локальні ступені його вершин за матрицею суміжності (табл.7.3), підраховуючи суми одиниць в рядках (або в стовпцях) матриці:

, , , , .

Результати підрахунків за обома матрицями збігаються.

Означення 7.10. Граф називається повним, якщо кожна пара його вершин сполучена ребром.

У звичайного повного графа на вершинах степені всіх вершин однакові і дорівнюють .

На рис.7.6 наведені повні графи на чотирьох вершинах.

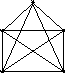
Приклад 7.6. Розглянемо повний граф на п’яти вершинах (рис.7.4).

Рис.7.4

Вправа 7.1.

Зображено графи (рис.7.19)

а)	б)	в)	г)
Рис.7.5

1) Подати ці графи всіма можливими способами подання.

2) Описати ці графи.

3) визначити локальні ступені всіх вершин графів.