1.2. Алгебра логіки
1.2.1. Поняття формули в алгебрі логіки
Як і в елементарній алгебрі, так і в алгебрі логіки, виходячи з елементарних функцій, можна будувати формули.
Літери, якими позначаються булеві змінні, позначки логічних операцій та дужки складають алфавіт алгебри логіки. За допомогою елементів алфавіту можна будувати формули алгебри логіки. Дамо математичне означення формули алгебри логіки.
Означення 1.5. Вираз, який складається з літер булевих змінних, позначок логічних операцій та дужок є формулою алгебри логіки, якщо він задовольняє наступним умовам:
1)
Будь-яка логічна змінна
є
формулою;
2) Якщо
і
- формули, то
а також
і
, які з’єднані будь-якою операцією з
табл.1.3, є формулою;
3) Інших формул немає.
Приклад 1.2. Такі вирази є формулами:
-
, -
, -
,
а ці вирази не є формулами:
-
– незакриті
дужки; -
– відсутній
символ булевої змінної; -
– відсутній
символ булевої змінної.
На прикладі дамо принцип підрахунку значень функції, яка може бути реалізована досить складною формулою.
Приклад
1.3.
Функція,
яку реалізує формула
будується
за три кроки (табл.1.5):
1.
2.
3.
|
Таблиця 1.5 |
||||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Приклад
1.4.
Функція,
яку реалізує формула
будується також за три кроки (табл.1.6):
1.
2.
3.
|
Таблиця 1.6 |
|||||
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Продовження таблиці 1.6 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
Означення
1.6.
Якщо
формула
описує функцію
,
то кажуть, що формулі
відповідає функція
або формулі
зіставлена функція
.
Якщо функція
відповідає формулі
,
то кажуть також, що формула
реалізує функцію
Наприклад,
формула
реалізує функцію
.
Це видно з табл.1.7 а.
|
Таблиця 1.7 а |
|
Таблиця 1.7 б |
||||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
Саме
таку таблицю істинності має й функція,
яка відповідає формулі
,
тобто й формула
реалізує функцію
,
(див. табл.1.7 б.).
Розглянемо
формули
,
і
.
Як видно з таблиць істинності (див.
табл.1.8.а),б),в)) перші дві мають завжди
значення змінної
,
а остання
завжди дорівнює 0.
|
Таблиця 1.8 а |
|
Таблиця 1.8 б |
|
Таблиця 1.8 в |
||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
0 |
|
0 |
1 |
0 |
|
1 |
1 |
|
1 |
1 |
|
1 |
0 |
0 |
Таким
чином, різні формули можуть реалізувати
одну й ту ж саму функцію. Більш того,
таких формул чимала кількість. Наприклад,
використовуючи доведені у табл.1.4. і
1.8. а), б), в), рівності
,
та
маємо
і
т.д.
Адже, наприклад, всього функцій від двох змінних існує 16, а формул, які їм відповідають, велика кількість. Проте, всі формули, які відповідають одній і тій самій функції, мають одну і ту саму таблицю істинності. Про такі формули кажуть, що вони рівносильні. Про рівносильні формули буде далі.
Вправа 1.1.
1. Для функцій, що реалізовані формулами побудувати таблиці істинності
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
2.
Визначити значення функції, яка
реалізована формулою
,
на наборах (0, 0, 1), (1, 1, 0), (1, 1, 1):
-
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
. -
.
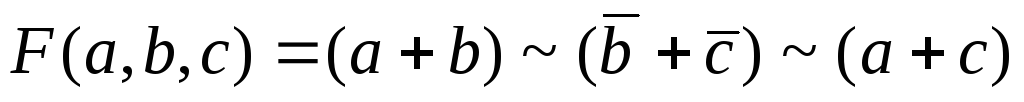