Определение площадей по переходной кривой

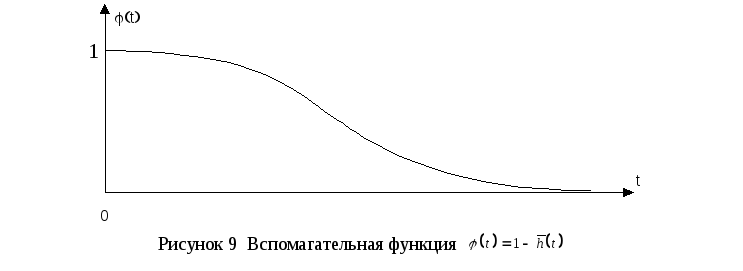
Введем в рассмотрение вспомогательную функцию , рисунок 9., определяемую формулой

(35)

Определим изображение по Лапласу . Принимая во внимание формулу (6) получим

(36)

Разложим в ряд по степеням в точке =0:

, (37)

где .

Коэффициенты разложения носят название моментов вспомогательной функции и могут быть вычислены непосредственно по графику .

Установим связь моментов с функцией . Запишем формулу прямого преобразования Лапласа для :

. (38)

Дифференцируя формулу (19) по последовательно раз получим:

(39)

Подставляя в (38) и (39) значение и сравнивая полученные выражения с формулами для моментов (37), получим:

(40)

Как видно из формул (40) моменты могут быть вычислены по известной функции . Установим связь между моментами и площадями .

Преобразуем формулу (36),

,

или

.

Отсюда следует,

. (41)

Подставляя разложения (37) и (24) в (41) получим

,

или

(42)

Умножая и приводя подобные члены, получим

. (43)

Из (43) следует,

(44)

Из последних уравнений получаем рекуррентные формулы для вычисления площадей:

(45)

Таким образом, алгоритм оценки параметров модели может быть записан следующим образом,

(46)

где ;

(47)

и

,

Вычисление моментов численными методами

Для вычисления интегралов в формулах (46) может быть использован метод трапеций. Бесконечный предел интегрирования в (46) заменяется конечным:

. (49)

Значение , рисунок 11, выбирается так, чтобы .

Интервал разбивается на равносторонних интервалов,

. (50)

Число интервалов разбиения выбирается таким, чтобы на каждом интервале мало отличалось от отрезка, соединяющего соседние точки.

Согласно формуле трапеций интеграл вида,

, (51)

заменяется суммой,

, (52)

где .

Для вычисления моментов (49) формула (52) принимает вид

(53)

Формулы (34) используются в программе Simou.exe [3] для расчета параметров модели.

Дадим оценку точности метода площадей. На рисунке 12 приведены графики функций для значений . Моменты , , пропорциональны площади под графиком , формулы (46), (49). При практических расчетах моментов вносится погрешность, обусловленная конечностью интервала интегрирования. Величина погрешности пропорциональна «отброшенной» площади, на рисунке 12, она заштрихована. Если для функции отброшенная площадь практически равна нулю и не влияет на точность вычисления момента , то для старших моментов отброшенная площадь и, соответственно, погрешность вычислений возрастает. Для обеспечения приемлемой точности модели на практике ограничиваются вычислением не более 3-х, 4-х моментов (площадей), что ограничивает порядок модели.

T_п

t

0

Рисунок 12. Оценка точности вычисления моментов

Временные характеристики

Временной характеристикой объекта называется его реакция на типовой апериодический сигнал. В качестве входных сигналов чаще всего используют ступенчатую функцию или её производную - - функцию. Реакция объекта или любого динамического звена на ступенчатую функцию единичной амплитуды (единичную ступенчатую функцию) называется переходной характеристикой объекта (звена) h(t). Реакцию объекта на ступеньку произвольной амплитуды х₀ называют кривой разгона объекта (рис.4). Для получения переходной характеристики из кривой разгона у(t) следует разделить каждую ординату кривой разгона на амплитуду ступеньки:

Аппроксимация переходных характеристик объектов регулирования.

Задача аппроксимации включает три этапа.

1. Выбор аппроксимирующей передаточной функции.

Переходные характеристики объектов с самовыравниванием и сосредоточенными параметрами аппроксимируют дробно-рациональной передаточной функцией в общем случае с чистым запаздыванием вида:

(7)

Для объектов без самовыравнивания в знаменателе передаточной функции (7) сомножителем добавляется переменная преобразования Лапласа р – признак интегрирующего звена.

Как показывает практика, удовлетворительная точность аппроксимации достигается при использовании моделей, для которых n=1,2,3, а n-m=1 при отсутствии точки перегиба в кривой разгона и n-m2 при её наличии.

2. Определение коэффициентов аппроксимирующей передаточной функции. (См. ниже)

3. Оценка точности аппроксимации.

Для оценки точности аппроксимации необходимо построить расчётную характеристику и определить максимальную ошибку аппроксимации. Выражения для переходных характеристик, соответствующих некоторым аппроксимирующим передаточным функциям, приведены в табл.1. При расчётах на ЭВМ в выражениях для переходных характеристик следует перейти к дискретному времени t=iΔt (Δt – интервал дискретности отсчётов), а при наличии в модели (7) чистого запаздывания к аргументу

Аппроксимация переходных характеристик объектов

с самовыравниванием инерционным звеном первого порядка с запаздыванием

а) Графический способ (метод касательной)

Передаточная функция ищется в виде:

(8)

Для определения τ и Т к переходной характеристике (рис.15) проводят касательную АВ в точке перегиба С (точке перегиба соответствует максимальный угол между касательной и осью абсцисс)

В y t

Отрезок ОА, отсекаемый касательной на оси абсцисс, принимается за время чистого запаздывания :

ОА

Длина подкасательной (проекция отрезка АВ на ось абсцисс) принимается за Т:

Т=АD

Коэффициент передачи К находится как отношение приращений выходной и входной величин в установившемся режиме:

(9)

б) Интерполяционный способ

Кривая разгона предварительно нормируется от 0 до 1 по формуле

(10)

Н

а нормированной кривой (рис.16) выбираются две точки А и В (узлы интерполяции), через которые должна проходить расчётная кривая.

1

В

А

Рис. 16.

t

0

t_A t_B

Нормированная переходная характеристика звена с передаточной функцией (8) равна

(11)

Записывая выражение (11) для точек А и В получаем систему двух уравнений с двумя неизвестными:

Разрешая эту систему относительно и Т, получаем:

Аппроксимация переходных характеристик объектов регулирования

звеном n-ного порядка

Поскольку рассматриваемый ниже метод предназначен для аппроксимации переходных характеристик объектов без чистого запаздывания и с самовыравниванием, то из кривой разгона необходимо предварительно исключить составляющие, соответствующие звеньям чистого запаздывания и интегрирующему, если таковые имеются.

Для исключения составляющей, обусловленной чистым запаздыванием, следует все абсциссы кривой разгона уменьшить на величину чистого запаздывания (т.е. перенести начало координат вправо на ). При этом в передаточной функции объекта с чистым запаздыванием

У

A

C

частку АВ переходной характеристики без запаздывания (рис.17) соответствует переходная функция .

B

Y₁(t)

y

y(t)

t

0

t

B

A

-y₂(t)

При аппроксимации переходной характеристики объекта без самовыравнивания она представляется в виде разности двух характеристик (рис.18):

Для этого проведём асимптоту ВС к установившемуся участку характеристики и луч ОА параллельный ВС. Вычитая y₁(t )из y(t), находим –y₂(t). y₁(t)- переходная характеристика интегрирующего звена с передаточной функцией

Коэффициент по-прежнему находится по формуле (15):

y₂(t) – переходная характеристика объекта с самовыравниванием. Ей соответствует передаточная функция . В силу линейности преобразования Лапласа передаточная функция объекта, соответствующая характеристике y(t), равна:

Коэффициенты передаточной функции могут быть найдены описываемым ниже методом.

Приводя выражение для к общему знаменателю, получаем искомую передаточную функцию объекта без самовыравнивания.

Определение коэффициентов передаточной функции объекта методом площадей Симою

Метод предназначен для определения коэффициентов дробно-рациональной передаточной функции объекта вида

(16)

На практике, как отмечалось, n=1,2,3; m=0,1. Коэффициент передачи , как всегда, определяется по формуле (9).

Для упрощения расчётов нормируем кривую разгона объекта в диапазоне 0-1 по формуле (10). Для нормированной кривой при единичном входном воздействии .

Запишем выражение обратное передаточной функции (16) и разложим его в бесконечный ряд по степеням р:

(17)

Приводя (17) к общему знаменателю и приравнивая коэффициенты при одинаковых степенях р, находим:

в частном случае при m=0

(19)

Числитель и знаменатель искомой передаточной функции (16) содержат (n+m) неизвестных коэффициентов, поэтому для их нахождения нужно, чтобы система (18) ( или в частном случае (19)) содержала столько же уравнений.

Итак, система (18) (или (19)) позволяет определить коэффициенты передаточной функции (16) через неизвестные пока коэффициенты разложения S_k.

Для определения последних рассмотрим изображение по Лапласу отклонения нормированной переходной характеристики от установившегося значения:

(20)

Из (20) находим

или с учётом определения преобразования Лапласа (3):

(21)

Раскладывая функцию в ряд по степеням pt:

можем представить интеграл в выражении (21) в виде суммы интегралов:

(22)

Подставляя разложения (17) и (22) в (21), перемножая степенные ряды от p и приравнивая в результирующем соотношении коэффициенты при одинаковых степенях р, получаем следующие выражения для коэффициентов S_k.

При практических расчётах интегралы (23) определяются численными методами. Например, при использовании метода трапеций выражения для коэффициентов S_k приобретают вид:

где - интервал дискретности отсчётов нормированной переходной характеристики,

N- число точек переходной характеристики .

С геометрической точки зрения коэффициент S₁ есть площадь , ограниченная кривой и линией установившихся значений. S₂ - есть площадь, взвешенная с весовой функцией и т. д. Таким образом, коэффициенты S_k есть некоторые взвешенные площади, что и определяет название метода.

Если при расчётах k-тый коэффициент S_k оказался отрицательным, необходимо в модели (16) уменьшить n на единицу или увеличить т (т.е. уменьшить разность (n-m)).

57