18.3. Аналитическая функция

Опр_3. Если ф-ия f =w(z) дифференцируема не только в т. Z, но и в некоторой её окрестности, то она называется аналитической в этой точке.

Ф-ия, аналитическая в каждой точке открытой области (без учета границы области) называется аналитической в этой области (голоморфной, моногенной, регулярной, правильной)

Опр_4. Те точки комплексной плоскости z в которых ф-ия f(z) аналитическая, назыв. Правильными точками ф-ии f(z). Те точки, в которых ф-ия не аналитическая (в частности таких не существует) называются особыми точками ф-ии f(z).

Пример: выяснить, является ли ф-ия w=z*Re z аналитичной:

W=(x+iy)x=x²+ixy => |U=x², V=xy| =>U’_x=2x V’_x=y

V’_y=0 U’_y=x

=>|U’_x=V’_y | => 2x = x => x=0 => z=0.

|U’_x=-V’_x | 0 = -y y=0

Условия КРЭДА позволяют по действительной или мнимой части восстановить саму аналитическую ф-ию w=f(z).

Иными словами, если одна из двух ф-ий или U(x,y) или V(x,y) задана, то другая ф-ия определяется из условия U’_x = V’_y, V’_x = - U’_y, т.е. находятся по её двум ч/п.

Пример: найти аналитическую ф-ию по её мнимой части: V(x,y) = 3x+2xy

V(x,y)=3x+2xy => |V’_x=3+2y U’_x=2x | =>

| V’_y=2x U’_y=3-2y |

U=∫U’_xdx = ∫2xdx + φ(x) = x² + φ(x)

U=∫U’_ydy=-∫(3+2y)dy + ψ(x) = -3y - y² + ψ(x)

U=x²-3y-y²+C

W=f(z)=U(x,y)+iV(x,y)=(x²-3y-y2+C)+i(3x+2xy)=

= | z=x+iy => x=(z+z)/2| = z² +3iz +C.

| z=x-iy => y=i(z-z)/2|

Л. 19 интегральное исчесление фкп.

19.1 Интеграл от ФКП(ИФКП):опр., сведение КРИ, теор. существ.

Пусть L=AB- дуга гладкой кривой или замкнутая кривая(контур),в точках которой опр.

Выполним следующие действия:

1. -разобъем АВ на n-частей(эл-тов дуг)точками z₀=A,z₁, z₂,…,z_n=B.;

–вычислим разности Δz_k=z_k-z_k-1(k=1,n).

–найдем диаметр разбиения дуги L(λ=max{|Δz_k|})

2. –выберем на каждой частичной дуге z_k-z_k-1 произв.точку C_k и составим сумму:

_k)* Δz_k (1)-комплексная интегральная сумма для ф-ции f(z) по кривой L в направлении от точки А до В.

Опр1. Если существует предел конечной интегральной суммы (1) при условии ,что λ→0(n→0),то он называется интегралом от ФКП по кривой L, и обозн.:

Δz_k.(2)

Теорема 19.1(о сведении ИФКП и КРИ)

ИФКП ф-ции f(z) вдоль кривой L=АВ сводится к выч. двух КРИ от действительных ф-ций 2-х действительных переем.:

(3)

u=u(x,y)=Re f(z)

v=v(x,y)=Im f(z)

1)ф-лу (3) можно записать в виде:

2)условия существов. ИФКП такие, как и у КРИ.

19.2(О существов.Ифкп)

1)Дуга L-гладкая

2)w=f(z) непрерывна на L,то существует конечный предел инт. суммы(1),т.е ФКП и этот предел не зависит от способа разбиения дуги L на части и выбора точек на них для составления инт.суммы.

Осн. св-ва ФКП:

1)

2)(при изменении пути инт. знак инт.меняется)

3)

4)

5)(если разбить дугу АВ точкой М по середине)

6)ИФКП по замкнутому контуру С не зависит от выбора точки с которой начинается обход контура.

Теорема 19.3(теор. Коши)

Если ф-я w=f(z) аналитична в обл.Д, то интеграл от нее по любому замкнутому контуру С, лежащему внутри обл.Д равен 0.

,()

Док-во: (),

Также выполн. услов.КРЭДА: ;

Согласно (3) инт. по замкнутому контуру:

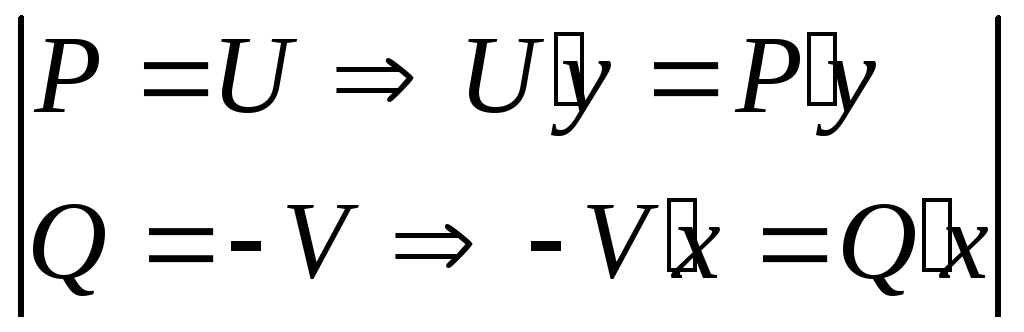
I2- доказывается аналогично, отсюда:

+i0=0, ч.т.д.

Следствие:если ф. f(z) аналитична в обл.Д ,то инт. от нее не зависит от формы кривой интегрирования, и его значение опред. только начальной точкой А и конечной т.В.Иными словами ИФКП от аналитичной ф-ции сохраняет постоянное значение по всем дугам лежащих внутри обл. Д, то независимо от того аналитическая она или нет выч. инт. Сводится к выч. двух КРИ от двух действительных ф-й 2х действ.переменных по ф-ле (3),при выч.инт.значительно упрощается если исходить из параметрического задания инт.:

L=АВ:

Тогда ур-е:

z(t)=x(t)+iy(t) – наз.: комплексного параметрического ур-нием кривой L.

Параметрич. ур-я окружности с центром в т. (х₀,у₀) и радиусом R имеет вид:

x=x₀+R cost

y=y₀+R sint,

ТогдаZ(t)=x₀+Rcost+i(y₀+Rsint)=(x₀+iy₀)+R(cost+isint)=z₀+ +R(cost+isint)=z₀+Re^it-комплексно параметрическое ур-ние окружности.Переход от ИФКП к КРИ осущ. по ф-ле:

(6)

Если же подинтегральная ф-я f(z) аналитична в обл.Д,то как и при интегрировании ф-ции действит.аргумента имеют место те же методы:

1)ф-ла Ньютона –Лейбница

,

где z_a, z_b- к/ч соотв. т.А и В кривой L.

2)метод инт. по частям:

3)метод замены переменой или подстановки:

, где

Z=g(w)-аналит.ф-я которая отображает кривую L пл-ти z в кривой L, в пл-ти Д.