13.4 Циркуляция поля

Опр 5. Линейным интегралом ВП наз КРИ (7)

Опр 6. Если кривая L замкнутая, то наз циркуляцией вектора поля по замкнутой линии (контуру): . (8)

Если ввести в рассмотрение вектор дифференциала дуги, то циркуляцию можно записать следующим

образом:

т.е. (9)

Циркуляция имеет простой физич. смысл: если кривая L расположена в силовом поле, то циркуляция выражает работу силы по перемещению материальной точки вдоль замкнутого контура L.

13.5 Ротор (вихрь) поля.

Опр 7. Ротором или вихрем ВП задаваемого векторной функцией

называется вектор, который обозн. и определяется функцией:

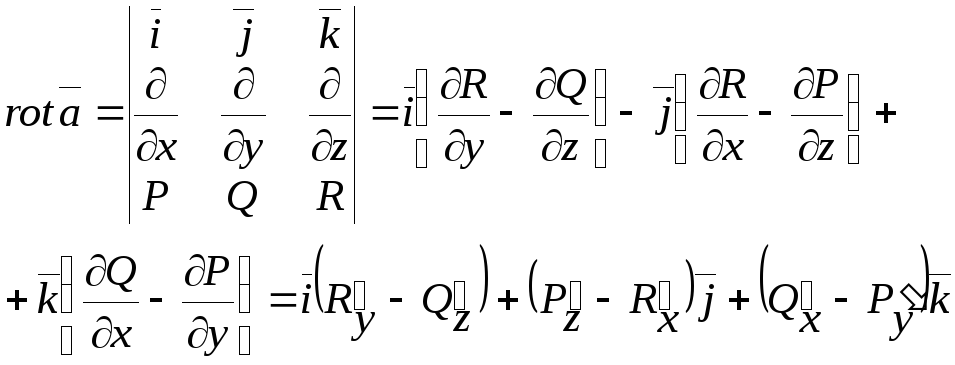
Следовательно можно сделать вывод: любое ВП порождает ВП ротора.

С помощью понятия циркуляции и ротора можно дать векторную форму записи формулы Стокса.

Учитывая связь между ПВИ-1 и ПВИ-2 запишем:

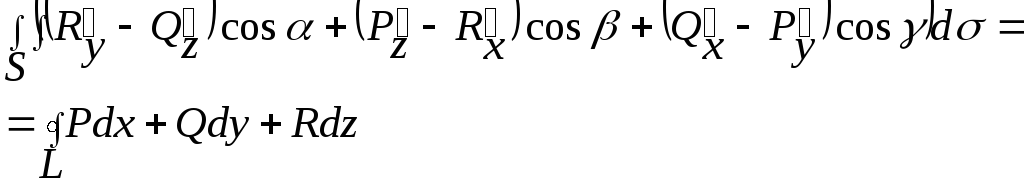
Формула Стокса в векторной форме: поток ротора ВП через поверхность S равен циркуляции вектора поля вдоль контура L, ограниченный поверхностью S.

Замечание :

Div и rot называются дифференциальными хар-ми ВП, а поток и циркуляция – интегральными хар-ми ВП.

14. Специальные векторные поля и их характеристики

14.1 Векторные дифференциальные операции 1 порядка

Основной дифференциальной операцией скалярного поля является а векторного поля -

Опр1. Операции нахождения называются векторными дифференциальными операциями 1 порядка (так как в них участвуют только ЧП 1-го порядка).

Опр 2. Символический вектор координатами которого являются операции частного дифференцирования наз. оператором Гамильтона или набла-оператором и обозначается . Таким образом, представляет собой:

Термин "символический" объясняется тем, что этот вектор приобретает конкретный смысл только комбинации со скалярными или векторными функциями. Умножение набла-оператора на число u или вектор производится по обычным правилам векторной алгебры, при этом с его координатами нужно обращаться как с обыкновенными дробями. Получим с помощью векторные дифференциальные операции 1 порядка:

1. Пусть u=u(M) – скалярная функция

Произведение на скалярную функцию равно градиенту этой функции: .

2. Пусть - векторная функция

Скалярное произведение на вектор поля равно div этого поля: .

3.

Векторное произведение набла-оператора на вектор поля равно : .

14.2 Векторные дифференциальные операции II – порядка

При применении набла-оператора к скалярному и векторному полям мы получаем новое поле к которому опять можно применить набла-оператор. В результате получим векторные дифференциальные операции II-порядка, их всего 5:

Получим выражения для этих операций.

Опр 3. Скалярный квадрат называется оператором Лапласа (лапласианом) или дельта-оператором.

1.

2.

3.

4.

5.

14.3 Соленоидальное векторное поле и его свойства

Опр 4. Векторное поле называется соленоидальным (трубчатым), если во всех его точках div поля равна 0

Примером такого поля может служить магнитное поле, создаваемое прямолинейным проводником по которому течет ток.

Основные свойства:

1.Соленоидальное поле является полем rot некоторого ВП, т.е. если , то существует такое ВП для которого

Утверждение, что поле ротора является соленоидальным доказывается легко