
- •Л.1 двойной интеграл в декатовых координатах.
- •1.1 Основные понятия и определения
- •1.2 Геометрический и физический смысл дви.
- •1.3 Основные свойства дви
- •1.4 Вычисление дви в декартовых координатах
- •Л.2 дви в полярных координатах. Замена переменных в дви.
- •2.1 Замена переменных в дви.
- •2.2 Дви в полярных координатах.
- •Лекция №3 Геометрические и физические приложения дви.
- •3.1 Геометрические приложения дви.
- •1) Вычисление объёмов пространственных тел.
- •2) Вычисление s плоской фигуры:
- •3.2 Физические приложения двойных интегралов.
- •1.Масса. Вычисление массы плоской фигуры.
- •2.Вычисление статических моментов и координат центра тяжести(центра масс) пластины.
- •3. Вычисление моментов инерции пластины.
- •Лекция 4 тройной интеграл
- •4.2 Основные св-ва три
- •4.3 Вычисление три в декартовых координатах
- •Л.5 криволинейные интегралы по координатам II рода – кри-II
- •5.1 Основные понятия и определения кри-II, теорема существования
- •5.2 Основные свойства кри-II
- •Л. 6. Связь между дви и кри. Свойства кри II-го рода связанные с формой пути интегрирования.
- •6.2. Условия (критерии) равенства нулю контурного интеграла.
- •6.3. Условия независимости кри от формы пути интегрирования.
- •Лекция №7 Условия независимости кри 2-го рода от формы пути интегрирования (продолжение)
- •Л.8 Геометрическая и физические приложения кри 2-го рода
- •8.1 Вычесление s плоской фигуры
- •8.2 Вычисление работы переменой силы
- •Лекция№9 Поверхностные интегралы по площади поверхности (пви-1)
- •9.2. Основные свойства пви-1
- •9.3.Гладкие поверхности
- •9.4.Вычисление пви-1 свидением к дви.
- •Л.10. Поверхностные интегралы по координатам (пви-2)
- •10.3. Основные свойства пви-2.
- •10.4. Вычисление пви-2
- •11.1.Формула Остроградского-Гаусса.
- •11.2 Формула Стокса.
- •11.3. Применение пви к вычислению объёмов тел.
- •Лк.12 элементы теории поля
- •12.1 Теор. Поля , осн. Понятия и определения.
- •12.2 Скалярное поле.
- •Лк 13. Векторное поле (вп) и его характеристики.
- •13.1 Векторные линии и векторные поверхности.
- •13.2 Поток вектора
- •Опр 3.Потоком вектора через поверхность s в заданном направлении наз. Пви от скалярного произведения вектора поля на единичный вектор нормали к поверхности s и обозначается п.
- •13.3 Дивергенция поля. Формула Остроградского-Гаусса.
- •13.4 Циркуляция поля
- •13.5 Ротор (вихрь) поля.
- •14. Специальные векторные поля и их характеристики
- •14.1 Векторные дифференциальные операции 1 порядка
- •Произведение на скалярную функцию равно градиенту этой функции: .
- •14.2 Векторные дифференциальные операции II – порядка
- •14.3 Соленоидальное векторное поле и его свойства
- •2.В соленоидальном поле поток вектора поля через замкнутую поверхность s равен 0
- •14.4 Потенциальное (безвихревое) вп и его свойства
- •14.5 Гармоническое поле
- •Л.15 элементы функции комплексного переменного. Комплексные числа(к/ч).
- •15.1. К/ч определение, геометрическое изображение.
- •15.2 Геометрическое представление к/ч.
- •15.3 Операция над к/ч.
- •15.4 Понятие расширенной комплексной z-пл.
- •16.1.Последовательность комплексных чисел определение, критерий существования.
- •16.2Арифметические свойства приделов комплексных чисел.
- •16.3 Функция комплексного переменного: определение, непрерывность.
- •Л.17 Основные элементарные ф.-ции комплексного переменного (фкп)
- •17.1.Однозначные элементарные фкп.
- •Л.18 Дифференцирование фкп. Аналитическая ф-ия
- •18.1. Производная и дифференциал фкп: основные понятия.
- •18.2. Критерий дифференцируемости фкп.
- •18.3. Аналитическая функция
- •Л. 19 интегральное исчесление фкп.
- •19.2(О существов.Ифкп)
- •19.4 Теорема(интегральная ф-я Коши)
- •19.5Теорема(обобщенная ф-ла Коши)
- •Л.20. Геометрический смысл модуля и аргумента производной. Понятие о конформном отображении.
- •Л.21. Ряды в комплексной области.
- •21.2 Числовые ряды (чр):
- •21.2 Степенные ряды (ср):
- •21.3 Ряд Тейлора:
- •21.4 Ряд Лорана:
- •Содержание
- •1.1 Основные понятия и определения
- •1.2 Геометрический и физический смысл дви.
Л.1 двойной интеграл в декатовых координатах.
1.1 Основные понятия и определения
Рассмотрим на плоскости ХОУ замкнутую область Д, т.е. такую область, которая ограничена замкнутой линией Г границей области, причем точки лежащие на границе принадлежат Д.
Пусть функция z=f(x,y) непрерывна в области Д.

1. Разобьем область Д произвольным образом на n-равных областей (площадок) Дi (i=1,n), площади которых обозначим через ∆Si. Наибольшее расстояние между двумя точками каждой площадки назовем диаметром площадки. А наибольший среди них – диаметром разбиения области Д.
λ=max{λi}
2.Выберем
на каждой площадке Дi
произвольную точку Mi(Xi,Yi),
умножим значение функции в этой точке
f(Xi,Yi)
на ∆Si
и составим сумму всех таких произведений.![]()
![]()
f(X1,Y2)*
∆S1+
f(X2,Y2)*
∆S2+……+f(Xn,Yn)*
∆Sn=![]()
![]() (1)
(1)
Опр.1 сумма (1) наз. интегральной суммой для функции f(X,Y) в области Д.
Опр.2 если существует конечный предел интегральной суммы (1) при n->∞,так что диаметр разбиения λ->0 , то он называется двойным интегралом от функции f(x,y) по области Д и обозначается:
![]() где
где
![]() -символ
двойного интеграла
-символ
двойного интеграла
Д-область интегрирования
f(x,y)-подынтегральная функция
х,у – переменные интегрирования
ds –элемент площади
Таким образом
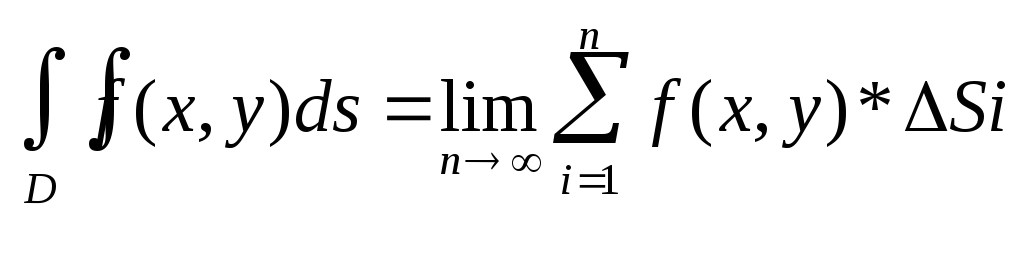
Теорема1: (Достаточное условие существования двойного интеграла) если функция z=f(x,y) непрерывна в рассматриваемой области Д, то существует конечный предел интегральной суммы (1) (т.е. ДВИ) и этот предел не зависит от способа разбиения области Д на площадки Дi и от выбора точек на них для составления интегральной суммы.
Из теоремы 1 следует, что разбиение области Д на площадки можно осуществить самым простым способом – линиями параллельными координатным осям.
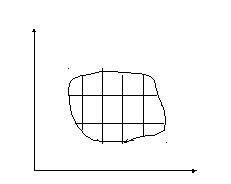
Тогда площадка Дi-прямоугольник, со сторонами ∆Х, ∆У. ∆S=∆x*∆y,т.к. для независимых переменных х и у, ∆х=dx, ∆y=dy.
Ds=∆S=∆x*∆y=dx*dy.
1.2 Геометрический и физический смысл дви.
Задача 1:
Рассмотрим тело, ограниченное сверху поверхностью Z=f(x,y)=>0, снизу- областью Д плоскости X0Y, а сбоку – цилиндрической поверхностью, образующая которой параллельна оси OZ, а направляющей служит граница области D.
Такое тело наз. цилиндрическим.
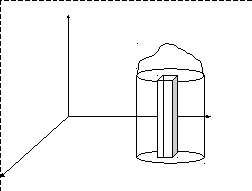
Каждое
слагаемое f(Xi,Yi)*∆Si
интегральной суммы (1) представляет
собой Vi
![]() прямой призмочки с высотой f(Xi,Yi)
и площадки основания
прямой призмочки с высотой f(Xi,Yi)
и площадки основания
![]()
![]() ,
,
а
вся интегральная сумма (1)
![]() объему
всего цилиндрического тела
объему
всего цилиндрического тела
![]() (3)
(3)
Равенство (3) будет тем точнее, чем больше n (число площадок) и чем меньше ∆Si, будет равно
![]() (4)
(4)
Геометрический смысл двойного интеграла ДВИ от неотрицательной функции Z=f(x,y) равна Vц.т.
Vц.т.=
![]()
Задача 2
Пусть
Д-тонкая плоская неоднородная пластинка
поверхностная плотность которой
![]() явл.
непрерывной функцией координат точки,
т.е.
явл.
непрерывной функцией координат точки,
т.е.
![]() =
=![]() (X,Y)
(X,Y)
Физический смысл ДВИ:
ДВИ
от поверхностной плотности
![]() (Х,У)
тонкой пластинки Д численно равен массе
этой пластинки
(Х,У)
тонкой пластинки Д численно равен массе
этой пластинки
![]() (5)
(5)
1.3 Основные свойства дви
Сравнивая определения ДВИ и ОИ можно сделать вывод, что принципиально они не отличаются, поэтому и их свойства будут аналогичными.
1.![]() с=const
с=const
2.![]()
3.
Если область Д разбить на 2 части Д1 и
Д2, такие что Д1![]() Д2=Д,
то
Д2=Д,
то
![]()
4.
![]()
![]()
