Формула Бернуллі

Якщо виконується n незалежних випробувань, у кожному з яких подія A відбувається з імовірністюp, то ймовірність того, що подія A настане m разів, визначається за формулою ;  . 

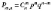30. Зрізана піраміда Зрізаною пірамідою називається многогранник, який залишиться, якщо від піраміди відділити площиною, яка паралельна основі, піраміду з тією ж вершиною. Теорема. Площина, яка паралельна основі піраміди й перетинає її, відтинає подібну піраміду. Зверніть увагу: щоб правильно зобразити зрізану піраміду, треба починати із зображення вихідної повної піраміди (див. рисунок). Основи зрізаної піраміди — подібні многокутники. Бічні грані — трапеції. 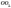 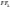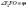— висота зрізаної піраміди,  — висота бічної грані,  — кут нахилу бічного ребра до площини основи (будь-якої),  — кут нахилу бічної грані до площини нижньої основи. Правильна зрізана піраміда — це зрізана піраміда, яку дістали з правильної піраміди. Її бічні ребра рівні й нахилені до площини основи під одним і тим самим кутом. Її бічні грані дорівнюють рівнобічній трапеції і нахилені до площини нижньої основи під одним і тим самим кутом. Висоти бічних граней піраміди називаються апофемами. Бічна поверхня правильної зрізаної піраміди дорівнює добутку півсуми периметрів основ і апофеми. 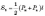, де Pн і Pв — периметри відповідних основ, l — апофема. На рисунках зображені фігури, які буває дуже корисним розглянути при розв’язуванні задач на зрізану піраміду. ; 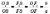.  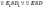;    — прямокутна трапеція. — висота зрізаної піраміди.  — висота бічної грані. У випадку, коли зрізана піраміда правильна, відрізки OD і  є радіусами описаного кола, а OF і 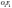— радіусами вписаного кола для нижньої і верхньої основи відповідно.

Об’єм зрізаної піраміди (див. рисунок) дорівнює 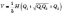, де H — висота,  — площа нижньої основи,  — площа верхньої основи. Об’єми подібних тіл відносяться як куби їх відповідних лінійних розмірів.