- •Властивості
- •Властивості
- •16. Зростаючі й спадні функції
- •Екстремуми функції
- •19. Скалярний добуток векторів
- •21. Перпендикуляр і похила
- •Властивості похилих
- •Перпендикуляр і похила
- •Теорема про триперпендикуляри
- •23. Паралелепіпед
- •26. Конус
- •27. Зрізаний конус
- •28. Куля
- •Площа круга
- •29. Основні поняття теорії імовірностей
- •Формула Бернуллі
16. Зростаючі й спадні функції
Функція
називається зростаючою на
деякому інтервалі, якщо для будь-яких
двох значень аргументу з цього інтервалу
більшому значенню аргументу відповідає
більше значення функції.
Функція
називається спадною на
деякому інтервалі, якщо для будь-яких
значень аргументу з цього інтервалу
більшому значенню аргументу відповідає
менше значення функції.
Приклади
1)
y = x2.
 Функція
зростаюча при
Функція
зростаюча при  (див.
рисунок).
Функція
спадна при
(див.
рисунок).
Функція
спадна при  .
Функція
парна.
2)
.
Функція
парна.
2)
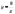 .
.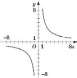 Функція
непарна (див. рисунок), спадна при
Функція
непарна (див. рисунок), спадна при 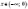 і
при
і
при 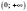 .
Зверніть
увагу: не можна сказати, що функція
.
Зверніть
увагу: не можна сказати, що функція 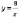 спадає
на проміжку
спадає
на проміжку  або
на всій області визначення. Дійсно,
візьмемо x1=-4, x2=2, x2>x1.
За означенням спадної функції, повинна
виконуватись умова
або
на всій області визначення. Дійсно,
візьмемо x1=-4, x2=2, x2>x1.
За означенням спадної функції, повинна
виконуватись умова  .
Однак
.
Однак 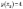 ,
, 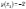 ,
тобто
,
тобто 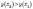 .
.
Екстремуми функції
Точку x0
називають точкою
мінімуму функції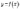 ,
а саме число
,
а саме число 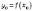 — мінімумом
функції,
якщо існує інтервал
— мінімумом
функції,
якщо існує інтервал 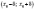 ,
,  ,
на якому функція
,
на якому функція 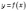 визначена
і
визначена
і 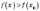 для
всіх
для
всіх 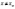 із
цього інтервалу.
Точку
із
цього інтервалу.
Точку  називають точкою
максимуму функції
називають точкою
максимуму функції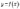 ,
а саме число
,
а саме число 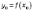 — максимумом
функції,
якщо існує інтервал
— максимумом
функції,
якщо існує інтервал  ,
,  ,
на якому функція
,
на якому функція 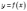 визначена
і
визначена
і  для
всіх
для
всіх  із
цього інтервалу.
Загальна
назва для точок максимуму і мінімуму
— точки
екстремуму,
а для значень функції в цих точках
— екстремуми
функції.
У
багатьох випадках графік функції можна
побудувати за допомогою геометричних
перетворень графіка відомої функції,
через яку виражається дана.
із
цього інтервалу.
Загальна
назва для точок максимуму і мінімуму
— точки
екстремуму,
а для значень функції в цих точках
— екстремуми
функції.
У
багатьох випадках графік функції можна
побудувати за допомогою геометричних
перетворень графіка відомої функції,
через яку виражається дана.
17. Диференційована функція F(x), називається первісною для функції f(x), на заданому проміжку, якщо для всіх іксів із цього проміжку виконується рівність: F’(x)=f(x). Сукупність всіх первісних F(x)+c для функції f(x) на даному інтервалі називають неозначеним інтегралом.
18. Криволінійною трапецією – називається фігура обмежена графіком неперервної невідємної функція y=f(x), x Є (a;b), прямими x=a, x=b cта відрізком осі Оx
19. Скалярний добуток векторів
Скалярним
добутком векторів 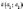 і
і 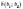 називається
число
називається
число 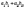 .
Позначення:
.
Позначення: 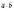 .
.
 .
Очевидно, що
.
Очевидно, що  .
Розподільна
властивість скалярного добутку:
.
Розподільна
властивість скалярного добутку:  .
Кутом
між ненульовими векторами
.
Кутом
між ненульовими векторами  і
і 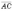 називається
кут BAC.
Кутом між будь-якими двома ненульовими
векторами
називається
кут BAC.
Кутом між будь-якими двома ненульовими
векторами  і
і  називається
кут між векторами, що дорівнюють даним
і мають спільний початок. Вважають, що
кут між однаково напрямленими векторами
дорівнює 0.
Теорема
1. Скалярний добуток векторів дорівнює
добутку їхніх абсолютних величин і
косинуса кута між ними:
називається
кут між векторами, що дорівнюють даним
і мають спільний початок. Вважають, що
кут між однаково напрямленими векторами
дорівнює 0.
Теорема
1. Скалярний добуток векторів дорівнює
добутку їхніх абсолютних величин і
косинуса кута між ними:  (див.
рисунок).
(див.
рисунок).
 Звідси
Звідси 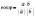 .
Теорема
2. Два ненульові вектори перпендикулярні
тоді й тільки тоді, коли їх скалярний
добуток дорівнює 0.
.
Теорема
2. Два ненульові вектори перпендикулярні
тоді й тільки тоді, коли їх скалярний
добуток дорівнює 0.
 ;
; 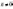 ;
; 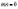

 .
.
20. Призмою називається многогранник, який складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників. Діагональним перерізом називається переріз площиною, яка проходить через два бічних ребра, що не належать одній площині. Бічною поверхнею призми називається сума площ бічних граней. Повна поверхня призми дорівнює сумі бічної поверхні і площ основ.

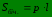
Об'єм призми нерівний. Він дорівнює добутку площі основи на висоту. Таким чином об'єм дорівнює:

де S — площа основи, h — висота. Об'єм правильної призми в основі якої є правильний n-кутник дорівнює:
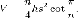
Площа
поверхні призми дорівнює  ,
де S —
площа основи, h —
висота, P —
периметр основи.
,
де S —
площа основи, h —
висота, P —
периметр основи.
Площа поверхні правильної призми в основі якої є правильний n-кутник дорівнює: