
- •Властивості
- •Властивості
- •16. Зростаючі й спадні функції
- •Екстремуми функції
- •19. Скалярний добуток векторів
- •21. Перпендикуляр і похила
- •Властивості похилих
- •Перпендикуляр і похила
- •Теорема про триперпендикуляри
- •23. Паралелепіпед
- •26. Конус
- •27. Зрізаний конус
- •28. Куля
- •Площа круга
- •29. Основні поняття теорії імовірностей
- •Формула Бернуллі
1.Функцією у = f(x) називається така відповідність між множинами D і Е, при якій кожному значенню змінної х відповідає одне й тільки одне значення змінної у.Область визначення — множина допустимих значень аргументу функції.Функція y=f(x) називаеться непарною якщо для будь якого значення x із області визначення використовуеться рівність f(-x)=-f(x).для парноъ f(-x)=f(x).
2.
Якщо
для довільної послідовності точок
взятої з області визначення відповідна
послідовність значень функції збігається
до того самого числа то це число називають
границею функції в
точці.Функція 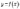 називається неперервною
в точці
називається неперервною
в точці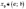 ,
якщо існує границя функції в цій точці
й вона дорівнює значенню функції в
точці
,
якщо існує границя функції в цій точці
й вона дорівнює значенню функції в
точці  .
.
Основні теореми про границь
1.Якщо
існують границі функції f(x)
і
 то існує також і границя їх суми що =
сумі границі данній функції,тобто:
то існує також і границя їх суми що =
сумі границі данній функції,тобто:

2.Якщо
існує границі функції f(х)
і 
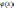 то існує також і границя їх добутку,що
= добутку границі данних функції,тоюто:
то існує також і границя їх добутку,що
= добутку границі данних функції,тоюто:

3.Якщо
існують границі функції f(x)
і
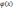
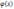 і границя
і границя 

відміння
від нуля то існує також і границя частки
цих функції 
 ,
від данних функції, тобто:
,
від данних функції, тобто: 
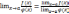
3. Коренем n-го степеня з числа a називається таке число, n-й степінь якого дорівнює a. Арифметичним коренем n-го степеня із невід'ємного числа а називається таке
невід'ємне число, n-й степінь якого дорівнює а.
Арифметичний корінь n-го степеня із числа а позначають так: . Число п
називають показником кореня, число а — підкореневим числом (виразом).
Якщо п = 2, то замість пишуть і називають арифметичним квадратним коренем.
Властивості
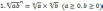

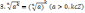
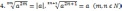
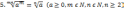

4.Означення
степенем числа 
 ,
a>0,
з раціональним показником
,
a>0,
з раціональним показником 
 де m
є Z,n
є
N
називається
число
де m
є Z,n
є
N
називається
число 
 ,
тобто:
,
тобто:
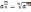 .
.
Властивості
1.
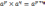
2.

3.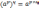
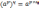
4.
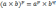
5.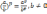
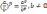
5.
 Степеневою
функцією називається функція
виду
Степеневою
функцією називається функція
виду 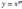
 де p —
постійне дійсне число, а
х
(основа)
— змінна.
де p —
постійне дійсне число, а
х
(основа)
— змінна.
1) р
= 1 -
пряма.
2) р
— натуральне, парне, р = 2n.
D(y)=R;
E(y)=[0;+∞).
Функція
спадає при х € (-∞; 0] і зростає при х €
[0; ∞).
Функція
парна, графік симетричний відносно осі
Оу. Окремий випадок: у = х2.
3) р
— натуральне, непарне, р = 2n + 1.
D(y)=R;
E(y)= R;
Функція
зростає на всій області визначення;
Функція
непарна, графік симетричний відносно
початку координат. Окремий випадок: у
= х3.
4) р
— ціле, від'ємне, непарне.
Нехай
р = -n.
Тоді,
за означенням степеня з від'ємним
показником,
 маємо:
маємо:
 функція
спадає при х € (-∞; 0) і (0;+ ∞);
функція
непарна, графік – гіпербола, симетрична
відносно початку координат і розміщена
у I і III координатних чвертях.
5) р
— ціле, від'ємне, парне.
функція
спадає при х € (-∞; 0) і (0;+ ∞);
функція
непарна, графік – гіпербола, симетрична
відносно початку координат і розміщена
у I і III координатних чвертях.
5) р
— ціле, від'ємне, парне.
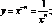 Нехай
р = -n
Нехай
р = -n
 функція
зростає при
функція
зростає при 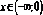 і
спадає при
і
спадає при  ;
функція
парна; графік – гіпербола, симетрична
відносно осі Оу.
;
функція
парна; графік – гіпербола, симетрична
відносно осі Оу.
6.
Показниковою функцією називається
функція виду 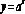 ,
де а — задане число, а>0, а
,
де а — задане число, а>0, а 1.
Властивості
показникової функції
1.
Областю визначення показникової функції
є всі дійсні числа.
2.
Множиною значень показникової функції
є всі додатні числа.
3.
Функція не є ні парною ні непарною,
оскільки а-х
1.
Властивості
показникової функції
1.
Областю визначення показникової функції
є всі дійсні числа.
2.
Множиною значень показникової функції
є всі додатні числа.
3.
Функція не є ні парною ні непарною,
оскільки а-х ах,
а-х
ах,
а-х -ах.
4.
Функція зростає на всій області
визначення, якщо а>1 і спадає на всій
області визначення, якщо 0 < а < 1. При
х=0 значення функції дорівнює 1, тобто
а0=1.
5.
Немає таких значень аргументу, при яких
значення показникової функції дорівнює
нулю, тобто у показникової функції
немає нулів.
6.
Показникова функція неперервна на всій
області визначення.
7.
Графік показникової функції:
-ах.
4.
Функція зростає на всій області
визначення, якщо а>1 і спадає на всій
області визначення, якщо 0 < а < 1. При
х=0 значення функції дорівнює 1, тобто
а0=1.
5.
Немає таких значень аргументу, при яких
значення показникової функції дорівнює
нулю, тобто у показникової функції
немає нулів.
6.
Показникова функція неперервна на всій
області визначення.
7.
Графік показникової функції:

 х
х
 х
7.
Логарифмом числа b за
основою а називається
показник степеня, до якого необхідно
піднести основу а,
щоб одержати число b.
Властивості
логарифмів
При
довільному а > 0 (а
х
7.
Логарифмом числа b за
основою а називається
показник степеня, до якого необхідно
піднести основу а,
щоб одержати число b.
Властивості
логарифмів
При
довільному а > 0 (а  1)
і довільних додатних х і у виконуються
такі властивості:
1.
Логарифм одиниці за основою а дорівнює
нулю
1)
і довільних додатних х і у виконуються
такі властивості:
1.
Логарифм одиниці за основою а дорівнює
нулю  2.
Логарифм а за основою а дорівнює
одиниці:
2.
Логарифм а за основою а дорівнює
одиниці:  3.
Логарифм добутку дорівнює сумі
логарифмів:
3.
Логарифм добутку дорівнює сумі
логарифмів: 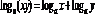 4.
Логарифм частки дорівнює різниці
логарифмів:
4.
Логарифм частки дорівнює різниці
логарифмів: 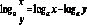 5.
Логарифм степеня дорівнює добутку
показника степеня на логарифм основи:
5.
Логарифм степеня дорівнює добутку
показника степеня на логарифм основи: 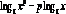 для
будь-якого дійсного числа р.
6.
Формула переходу від однієї основи
логарифма до іншої:
для
будь-якого дійсного числа р.
6.
Формула переходу від однієї основи
логарифма до іншої: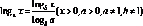 .
7.
.
7. 8.
8.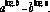
8.
Функцію

 називають
логарифмічною
функцією
з основою a.
Логарифмічна та показникова функції
є взаємно оберненими
називають
логарифмічною
функцією
з основою a.
Логарифмічна та показникова функції
є взаємно оберненими
Основні властивості логарифмічної функції y=logax.
1. Область визначення логарифмічної функції – множина R+ всіх додатних чисел. 2. Область значень логарифмічної функції – множина R всіх дійсних чисел. 3. Логарифмічна функція на всій області визначення R+ зростає, якщо a>0 і спадає, якщо 0<a<1.
9. Тригонометри́чні фу́нкції — це функції кута, особливо корисні при дослідженні та моделюванні періодичних подій. Вони можуть бути визначені як відношення двох сторін трикутника що містить кут, або як відношення координат точок по колу, або, більш загально, як нескінченні ряди, або як розв'язок диференційного рівняння.
10 Функція називається зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною


11.


12
.

13


14.Обернені тригонометричні функції — це математичні функції, що є оберненими до тригонометричних функцій.До обернених тригонометричних функцій відносять 6 функцій:
аркси́нус (arcsin) ;
аркко́синус (arccos);
аркта́нгенс (arctg; в іноземній літературі arctan)
-
арккота́нгенс (arcctg; в іноземній літературі arccot чи arccotan)
-
арксе́канс (arcsec)
-
арккосе́канс (arccosec; в іноземній літературі arccsc)
15. Похідною функції y=f(x), в даній точці х – називається границя відношення приросту функції до відповідного приросту аргументу, при умові, що приріст аргументу прямує до 0. Геометрична точка зору. Похідна функції y=f(x) при X прямує до Xo – це кутовий коефіцієнт дотичної до графіка функції в точці М(Xo; f(Xo)) k=tgl=f’(Xo) – k- кутовий коефіцієнт.
