
- •Властивості
- •Властивості
- •16. Зростаючі й спадні функції
- •Екстремуми функції
- •19. Скалярний добуток векторів
- •21. Перпендикуляр і похила
- •Властивості похилих
- •Перпендикуляр і похила
- •Теорема про триперпендикуляри
- •23. Паралелепіпед
- •26. Конус
- •27. Зрізаний конус
- •28. Куля
- •Площа круга
- •29. Основні поняття теорії імовірностей
- •Формула Бернуллі
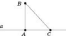
21. Перпендикуляр і похила
Нехай BA — перпендикуляр,
опущений із точки B на
пряму a,
а С —
будь-яка точка прямої a,
відмінна від A (див.
рисунок). Відрізок BC називається похилою,
проведеною з точки B до
прямої a.
Точка С називається основою
похилої.
Відрізок AС називається проекцією
похилої.
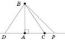
Властивості похилих
Теорема.
Коли з даної точки до прямої проведено
перпендикуляр і похилі, то будь-яка
похила більша від перпендикуляра; рівні
похилі мають рівні проекції, а з двох
похилих більша та, в якої проекція
більша.
На
рисунку BD, BC, BP —
похилі, AB —
перпендикуляр,  ;
;  ;
; .
.
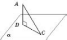
Перпендикуляр і похила
Перпендикуляром,
опущеним із даної точки на дану площину,
називається відрізок, що сполучає дану
точку з точкою площини й лежить на
прямій, перпендикулярній до площини.
Кінець цього відрізка, який лежить у
площині, називається основою
перпендикуляра. Відстанню
від точки до площини називається
довжина перпендикуляра, опущеного із
цієї точки на площину.
На
рисунку AB —
перпендикуляр; AC —
похила; BC —
проекція.
 Відстанню
від прямої до
паралельної їй площини називається
відстань від будь-якої точки цієї прямої
до площини.
Відстанню
між паралельними площинами називається
відстань від будь-якої точки однієї
площини до другої площини.
Похилою,
проведеною з даної точки до даної
площини, називається будь-який відрізок,
який сполучає дану точку з точкою
площини і не є перпендикуляром до
площини. Кінець відрізка, що лежить
у площині, називається основою
похилої.
Відрізок,
який сполучає основи перпендикуляра
й похилої, проведених з однієї і тієї
самої точки, називається проекцією
похилої.
Відстанню
від прямої до
паралельної їй площини називається
відстань від будь-якої точки цієї прямої
до площини.
Відстанню
між паралельними площинами називається
відстань від будь-якої точки однієї
площини до другої площини.
Похилою,
проведеною з даної точки до даної
площини, називається будь-який відрізок,
який сполучає дану точку з точкою
площини і не є перпендикуляром до
площини. Кінець відрізка, що лежить
у площині, називається основою
похилої.
Відрізок,
який сполучає основи перпендикуляра
й похилої, проведених з однієї і тієї
самої точки, називається проекцією
похилої.
Теорема про триперпендикуляри
Теорема 1. Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок). І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
22.

23. Паралелепіпед
Паралелепіпедом
називається призма, в основі якої лежить
паралелограм.
Усі
грані паралелепіпеда — паралелограми.
Грані
паралелепіпеда, які не мають спільних
вершин, називаються протилежними.
Теорема
1. Протилежні грані паралелепіпеда є
паралельними й рівними.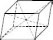 Паралелепіпед
залишається паралелепіпедом у всіх
випадках, коли за його основу вважаємо
довільну його грань (див. рисунок).
Теорема
2. Діагоналі паралелепіпеда перетинаються
в одній точці й точкою перетину діляться
навпіл.
Із
цього випливає, що точка перетину
діагоналей паралелепіпеда є його
центром симетрії.
Зверніть
увагу: у прямого паралелепіпеда є чотири
діагоналі, які попарно дорівнюють одна
одній.
На
рисунку
Паралелепіпед
залишається паралелепіпедом у всіх
випадках, коли за його основу вважаємо
довільну його грань (див. рисунок).
Теорема
2. Діагоналі паралелепіпеда перетинаються
в одній точці й точкою перетину діляться
навпіл.
Із
цього випливає, що точка перетину
діагоналей паралелепіпеда є його
центром симетрії.
Зверніть
увагу: у прямого паралелепіпеда є чотири
діагоналі, які попарно дорівнюють одна
одній.
На
рисунку  ;
;  .
Це
випливає з властивостей похилих,
оскільки
.
Це
випливає з властивостей похилих,
оскільки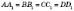 —
рівні перпендикуляри до площини
основи ABCD.
—
рівні перпендикуляри до площини
основи ABCD.
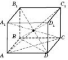 Якщо
дві діагоналі прямого паралелепіпеда
виходять із сусідніх вершин, то більша
з них та, яка проектується у більшу
діагональ основи, тобто таку діагональ
паралелограма, яка лежить проти тупого
кута. Отже, якщо на наведеному вище
рисунку вважати кут ABC тупим,
отримаємо
Якщо
дві діагоналі прямого паралелепіпеда
виходять із сусідніх вершин, то більша
з них та, яка проектується у більшу
діагональ основи, тобто таку діагональ
паралелограма, яка лежить проти тупого
кута. Отже, якщо на наведеному вище
рисунку вважати кут ABC тупим,
отримаємо  ,
, 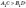 .
Прямий
паралелепіпед, у якого основою є
прямокутник, називається прямокутним
паралелепіпедом (див.
рисунок).
.
Прямий
паралелепіпед, у якого основою є
прямокутник, називається прямокутним
паралелепіпедом (див.
рисунок).
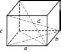 Усі
грані прямокутного паралелепіпеда —
прямокутники, які можна розбити на три
пари рівних між собою. Довільну грань
прямокутного паралелепіпеда можна
вважати його основою. Враховуючи, що
при паралельному проектуванні довільний
паралелограм може зображуватися
довільним паралелограмом, зображення
прямокутного паралелепіпеда ніяк не
відрізняється від зображеня будь-якого
прямого паралелепіпеда.
Довжини
непаралельних ребер називаються лінійними
розмірами (вимірами)
прямокутного паралелепіпеда.
Теорема
3. У прямокутному паралелепіпеді всі
діагоналі рівні. Квадрат діагоналі
дорівнює сумі квадратів трьох його
вимірів.
Усі
двогранні кути прямокутного паралелепіпеда
є прямими.
Прямокутний
паралелепіпед має три пари рівних між
собою діагональних перерізів. Кожний
із цих перерізів є прямокутником (див.
рисунки).
Усі
грані прямокутного паралелепіпеда —
прямокутники, які можна розбити на три
пари рівних між собою. Довільну грань
прямокутного паралелепіпеда можна
вважати його основою. Враховуючи, що
при паралельному проектуванні довільний
паралелограм може зображуватися
довільним паралелограмом, зображення
прямокутного паралелепіпеда ніяк не
відрізняється від зображеня будь-якого
прямого паралелепіпеда.
Довжини
непаралельних ребер називаються лінійними
розмірами (вимірами)
прямокутного паралелепіпеда.
Теорема
3. У прямокутному паралелепіпеді всі
діагоналі рівні. Квадрат діагоналі
дорівнює сумі квадратів трьох його
вимірів.
Усі
двогранні кути прямокутного паралелепіпеда
є прямими.
Прямокутний
паралелепіпед має три пари рівних між
собою діагональних перерізів. Кожний
із цих перерізів є прямокутником (див.
рисунки).
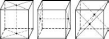 Кожна
пара перерізів перетинається по прямій,
яка проходить через точки перетину
діагоналей протилежних граней. Відрізки
між цими точками є паралельними й
дорівнюють одному з ребер прямокутного
паралелепіпеда.
Прямокутним
є трикутник, який утворюється діагоналлю
прямокутного паралелепіпеда, діагоналлю
бічної грані й стороною основи (див.
рисунок). Наприклад,
Кожна
пара перерізів перетинається по прямій,
яка проходить через точки перетину
діагоналей протилежних граней. Відрізки
між цими точками є паралельними й
дорівнюють одному з ребер прямокутного
паралелепіпеда.
Прямокутним
є трикутник, який утворюється діагоналлю
прямокутного паралелепіпеда, діагоналлю
бічної грані й стороною основи (див.
рисунок). Наприклад, 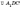
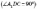 .
.
 Прямокутний
паралелепіпед має центр симетрії — це
точка перетину його діагоналей.
Він
також має три площини симетрії, які
проходять через центр симетрії паралельно
граням.
Прямокутний
паралелепіпед, у якого всі ребра рівні,
називається кубом.
Площина
будь-якого діагонального перерізу куба
є його площиною симетрії. Таким чином,
куб має дев’ять площин симетрії.
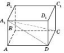
На
рисунку розглянемо взаємне розміщення
деяких елементів прямого паралелепіпеда:
Прямокутний
паралелепіпед має центр симетрії — це
точка перетину його діагоналей.
Він
також має три площини симетрії, які
проходять через центр симетрії паралельно
граням.
Прямокутний
паралелепіпед, у якого всі ребра рівні,
називається кубом.
Площина
будь-якого діагонального перерізу куба
є його площиною симетрії. Таким чином,
куб має дев’ять площин симетрії.
На
рисунку розглянемо взаємне розміщення
деяких елементів прямого паралелепіпеда:
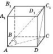
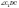 —
кут між діагоналлю бічної грані й
площиною основи (
—
кут між діагоналлю бічної грані й
площиною основи (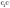 —
перпендикуляр,
—
перпендикуляр, 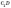 —
похила, СD —
проекція).
—
похила, СD —
проекція).
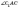 —
кут між діагоналлю прямого паралелепіпеда
й площиною основи (
—
кут між діагоналлю прямого паралелепіпеда
й площиною основи (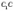 —
перпендикуляр,
—
перпендикуляр, 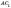 —
похила, АС —
проекція).
—
похила, АС —
проекція).
 —
кут нахилу діагоналі
—
кут нахилу діагоналі 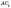 до
бічної грані
до
бічної грані 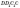 (AD —
перпендикуляр,
(AD —
перпендикуляр, 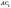 —
похила,
—
похила, 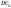 —
проекція).
Нехай
—
проекція).
Нехай 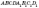 —
прямий паралелепіпед (див. рисунок),
де ABCD —
ромб. Проведемо його переріз площиною,
що проходить через діагональ основи BD і
вершину
—
прямий паралелепіпед (див. рисунок),
де ABCD —
ромб. Проведемо його переріз площиною,
що проходить через діагональ основи BD і
вершину  .
.
 У
перерізі отримаємо рівнобедрений
трикутник
У
перерізі отримаємо рівнобедрений
трикутник 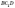 .
.
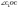 —
лінійний кут двогранного кута між
площинами основи й перерізу.
—
лінійний кут двогранного кута між
площинами основи й перерізу. 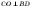 за
властивістю діагоналей ромба,
за
властивістю діагоналей ромба, 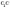 —
перпендикуляр,
—
перпендикуляр, 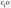 —
похила, СО —
проекція. За теоремою про три
перпендикуляри:
—
похила, СО —
проекція. За теоремою про три
перпендикуляри: 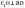 .
.
24. Піраміда
Пірамідою називається
многогранник, який складається з
плоского многокутника — основи піраміди,
точки, яка не лежить у площині основи
— вершини піраміди, і всіх відрізків,
що сполучають вершину піраміди з точками
основи. Відрізки, що сполучають вершину
піраміди з вершинами основи,
називаються бічними
ребрами.
Висота
піраміди —
перпендикуляр, опущений із вершини
піраміди на площину основи.
Піраміда
називаєтьсяn-кутною,
якщо її основою є n-кутник.
Трикутна піраміда називається
такожтетраедром. Бічна
грань піраміди —
трикутник. Однією з його вершин є вершина
піраміди, а протилежною стороною —
сторона основи піраміди.
На
рисунку SO —
висота піраміди. Тоді  —
кут між бічним ребром і площиною основи
(SO —
перпендикуляр, SА —
похила, OА —
проекція).
—
кут між бічним ребром і площиною основи
(SO —
перпендикуляр, SА —
похила, OА —
проекція).
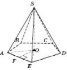 З
основи висоти піраміди (точки О)
проведемо перпендикуляр на сторону
основи (наприклад, АЕ).
Основу цього перпендикуляра (точку F)
з’єднаємо з вершиною піраміди (точкою S).
За теоремою про три перпендикуляри:
З
основи висоти піраміди (точки О)
проведемо перпендикуляр на сторону
основи (наприклад, АЕ).
Основу цього перпендикуляра (точку F)
з’єднаємо з вершиною піраміди (точкою S).
За теоремою про три перпендикуляри:  .
(SO —
перпендикуляр, SP —
похила, OF —
проекція,
.
(SO —
перпендикуляр, SP —
похила, OF —
проекція,  за
побудовою.) Отже,
за
побудовою.) Отже,  —
лінійний кут двогранного кута між
площиною бічної грані ASEі
площиною основи.
Для
розв’язування задач про піраміду дуже
важливо з’ясовувати, де розміщена
основа її висоти.
1.
Якщо виконується хоча б одна з таких
умов:
•
усі бічні ребра піраміди рівні;
•
усі бічні ребра нахилені до площини
основи під одним і тим самим кутом;
•
усі бічні ребра утворюють однакові
кути з висотою піраміди;
•
усі бічні ребра рівновіддалені від
основи висоти, — то основою висоти
піраміди є центр кола, описаного навколо
основи піраміди.
Бічне
ребро l,
висота H і
радіус R описаного
навколо основи кола утворюють прямокутний
трикутник:
—
лінійний кут двогранного кута між
площиною бічної грані ASEі
площиною основи.
Для
розв’язування задач про піраміду дуже
важливо з’ясовувати, де розміщена
основа її висоти.
1.
Якщо виконується хоча б одна з таких
умов:
•
усі бічні ребра піраміди рівні;
•
усі бічні ребра нахилені до площини
основи під одним і тим самим кутом;
•
усі бічні ребра утворюють однакові
кути з висотою піраміди;
•
усі бічні ребра рівновіддалені від
основи висоти, — то основою висоти
піраміди є центр кола, описаного навколо
основи піраміди.
Бічне
ребро l,
висота H і
радіус R описаного
навколо основи кола утворюють прямокутний
трикутник:
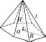 У
цьому випадку бічну поверхню можна
знайти за формулою
У
цьому випадку бічну поверхню можна
знайти за формулою 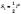
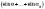 ,
де l —
довжина бічного ребра,
,
де l —
довжина бічного ребра,  ,
...
,
...  —
плоскі кути при вершині.
2.
Якщо виконується хоча б одна з таких
умов:
•
всі бічні грані нахилені до площини
основи під одним і тим самим кутом;
•
усі бічні грані мають однакові висоти;
•
висоти бічних граней утворюють однакові
кути з висотою піраміди;
•
бічні грані рівновіддалені від основи
висоти, — то основа висоти лежить у
центрі кола, вписаного в основу
піраміди.
На
рисунку
—
плоскі кути при вершині.
2.
Якщо виконується хоча б одна з таких
умов:
•
всі бічні грані нахилені до площини
основи під одним і тим самим кутом;
•
усі бічні грані мають однакові висоти;
•
висоти бічних граней утворюють однакові
кути з висотою піраміди;
•
бічні грані рівновіддалені від основи
висоти, — то основа висоти лежить у
центрі кола, вписаного в основу
піраміди.
На
рисунку  —
прямокутний
—
прямокутний 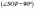 ,
,  —
радіус вписаного кола в ABCDEF;
—
радіус вписаного кола в ABCDEF;
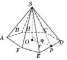
 —
висота піраміди, SP —
висота бічної грані;
—
висота піраміди, SP —
висота бічної грані;
 —
лінійний кут двогранного кута між
бічною гранню й площиною основи;
О —
центр вписаного в основу кола, тобто
точка перетину бісектрис ABCDEF.
У
цьому випадку
—
лінійний кут двогранного кута між
бічною гранню й площиною основи;
О —
центр вписаного в основу кола, тобто
точка перетину бісектрис ABCDEF.
У
цьому випадку 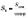 .
3.
Якщо бічне ребро перпендикулярне до
площини основи, то це ребро є висотою
піраміди (див. рисунки).
.
3.
Якщо бічне ребро перпендикулярне до
площини основи, то це ребро є висотою
піраміди (див. рисунки).
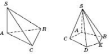 У
цьому випадку
У
цьому випадку  і
і — кути
нахилу бічних ребер SВ і SС відповідно
до площини основи.
— кути
нахилу бічних ребер SВ і SС відповідно
до площини основи.  є
лінійним кутом двогранного кута між
бічними гранями SAC і SBA.
є
лінійним кутом двогранного кута між
бічними гранями SAC і SBA.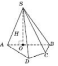 4.
Якщо бічна грань перпендикулярна до
площини основи (див. рисунок), то висотою
піраміди буде висота цієї грані (за
теоремою «Якщо пряма, яка лежить в одній
із двох перпендикулярних площин,
перпендикулярна до прямої їх перетину,
то вона перпендикулярна до другої
площини»).
4.
Якщо бічна грань перпендикулярна до
площини основи (див. рисунок), то висотою
піраміди буде висота цієї грані (за
теоремою «Якщо пряма, яка лежить в одній
із двох перпендикулярних площин,
перпендикулярна до прямої їх перетину,
то вона перпендикулярна до другої
площини»).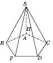 5.
Якщо дві бічні грані перпендикулярні
до площини основи, то висотою піраміди
є їх загальне бічне ребро.
5.
Якщо дві бічні грані перпендикулярні
до площини основи, то висотою піраміди
є їх загальне бічне ребро.
25. Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, — твірними циліндра. Основи циліндра рівні й лежать у паралельних площинах. Твірні циліндра паралельні й рівні. Бічна поверхня циліндра складається з його твірних. Поверхня — з основі бічної поверхні. Радіус циліндра — це радіус його основи. Висота циліндра — відстань між площинами його основ. Віссю циліндра називається пряма, яка проходить через центри основ. Вісь циліндра паралельна твірним. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр (далі просто «циліндр») можна дістати в результаті обертання прямокутника навколо сторони як осі. У прямому циліндрі висота дорівнює твірній. Перерізом циліндра площиною, паралельною його осі, є прямокутник. Дві його сторони — твірні циліндра, а дві інші — рівні й паралельні хорди основ.Осьовий переріз — переріз циліндра площиною, яка проходить через його вісь. Площина, паралельна осі циліндра, перпендикулярна до площин його основ
Об’єм циліндра
дорівнює добутку площі його основи та
висоти.
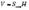 ;
;
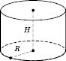
 .
.
