
- •Властивості
- •Властивості
- •16. Зростаючі й спадні функції
- •Екстремуми функції
- •19. Скалярний добуток векторів
- •21. Перпендикуляр і похила
- •Властивості похилих
- •Перпендикуляр і похила
- •Теорема про триперпендикуляри
- •23. Паралелепіпед
- •26. Конус
- •27. Зрізаний конус
- •28. Куля
- •Площа круга
- •29. Основні поняття теорії імовірностей
- •Формула Бернуллі
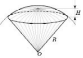
26. Конус
Круговим
конусом називається
тіло, яке складається з круга — основи
конуса,
точки, яка не лежить у площині цього
круга, — вершини
конуса і
всіх відрізків, що сполучають вершину
конуса з точками основи. Відрізки, що
сполучають вершину конуса з точками
кола основи, називаютьсятвірними
конуса.
Конус
називається прямим (далі
просто «конус»), якщо пряма, що сполучає
вершини конуса з центром основи,
перпендикулярна до площини основи.
Прямий
круговий конус можна розглядати як
тіло, утворене в результаті обертання
прямокутного трикутника навколо
його катета як осі.
Висота
конуса —
перпендикуляр, опущений із його вершини
на площину основи.
Віссю прямого
кругового конуса називається пряма,
яка містить його висоту.
Зверніть
увагу на рисунок нижче. Так звані
«контурні твірні» SA i SB є
дотичними до еліпса, який зображує
основу конуса, точки A і B не
є кінцями великої осі еліпса. Переріз
конуса площиною, яка проходить через
його вершину, — рівнобедрений трикутник,
у якого бічні сторони є твірними конуса,
а основою є хорда основи.
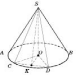 Розглянемо
переріз CSD.
Він перетинає основу конуса по
хорді CD.
Хорду CD видно
з центра основи під кутом COD,
а з вершини конуса — під кутом CSD.
Сам
переріз — рівнобедрений
Розглянемо
переріз CSD.
Він перетинає основу конуса по
хорді CD.
Хорду CD видно
з центра основи під кутом COD,
а з вершини конуса — під кутом CSD.
Сам
переріз — рівнобедрений  з
основою CD,
де
з
основою CD,
де  — твірні
конуса. Його ортогональною проекцією
на площину основи конуса є рівнобедрений
— твірні
конуса. Його ортогональною проекцією
на площину основи конуса є рівнобедрений 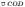 з
основою CD і
з
основою CD і  .
Відрізок OK є
бісектрисою, медіаною, висотою
.
Відрізок OK є
бісектрисою, медіаною, висотою  ,
відстанню від точки O до
хорди CD.
Відрізок SK є
бісектрисою, медіаною, висотою
,
відстанню від точки O до
хорди CD.
Відрізок SK є
бісектрисою, медіаною, висотою  та
відстанню від вершини конуса S до
хорди CD.
та
відстанню від вершини конуса S до
хорди CD.  є
лінійним кутом двогранного кута між
площиною перерізу й площиною основи.
Отже,
є
лінійним кутом двогранного кута між
площиною перерізу й площиною основи.
Отже, 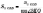 ,
,  —
кути нахилу твірної конуса до його
основи.
Площа
бічної поверхні конуса обчислюється
за формулою
—
кути нахилу твірної конуса до його
основи.
Площа
бічної поверхні конуса обчислюється
за формулою 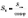 ,
де Sосн
— площа основи,
,
де Sосн
— площа основи,  —
кут нахилу твірної конуса до його
основи.
—
кут нахилу твірної конуса до його
основи.
Об’єм конуса (див.
рисунок) дорівнює одній третині добутку
площі його основи та висоти.
 .
.

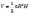 .
.
27. Зрізаний конус
Площина,
паралельна площині основи конуса,
перетинає конус по кругу, а бічну
поверхню — по колу з центром на осі
конуса. Така площина відтинає від конуса
менший конус. Частина, що залишилась,
називається зрізаним
конусом (див.
рисунок):
 ;
;
 Зверніть
увагу на осьовий переріз зрізаного
конуса. Це рівнобічна трапеція, в якої
основи — діаметри основ зрізаного
конуса, бічні сторони — твірні, висота
— висота зрізаного конуса.
Отже,
Зверніть
увагу на осьовий переріз зрізаного
конуса. Це рівнобічна трапеція, в якої
основи — діаметри основ зрізаного
конуса, бічні сторони — твірні, висота
— висота зрізаного конуса.
Отже,  .
Sб
.
Sб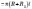 ,
де
,
де  ,
— формула для обчислення бічної поверхні
зрізаного конуса.
,
— формула для обчислення бічної поверхні
зрізаного конуса.
Об’єм зрізаного
конуса (див.
рисунок):
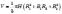 .
.

28. Куля
Кулею називається
тіло, що складається з усіх точок
простору, які розташовані від даної
точки на відстані, що не більша за дану.
Ця точка називається центром
кулі,
а дана відстань — радіусом
кулі.
Межа кулі називається кулевою
поверхнею,
або сферою.
Відрізок, що сполучає дві точки кульової
поверхні й проходить через центр кулі,
називається діаметром.
Куля є тілом обертання, яке утворюється
під час обертання півкруга навколо
його діаметра як осі. Будь-який переріз
кулі площиною є круг. Центр цього круга
є основою перпендикуляра, опущеного з
центра кулі на січну площину.
На
рисунку у 
 , OA —
радіус кулі,
, OA —
радіус кулі, 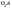 —
радіус перерізу,
—
радіус перерізу,  —
відстань від центра кулі до площини
перерізу (d).
—
відстань від центра кулі до площини
перерізу (d).
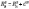 .
. Площина,
яка проходить через центр кулі,
називається діаметральною
площиною.
Переріз кулі діаметральною площиною
називається великим
кругом,
а переріз сфери — великим
колом,
або екватором.
Будь-яка
діаметральна площина кулі є її площиною
симетрії. Центр кулі є її центром
симетрії.
Площина,
яка проходить через точку А кульової
поверхні та є перпендикулярною до
радіуса, проведеного в точку А,
називається дотичною
площиною.
Точка А називається точкою
дотику.
Дотична
площина має з кулею тільки одну спільну
точку — точку дотику.
Пряма,
яка належить дотичній до кулі площині
й проходить через точку дотику,
називаєтьсядотичною
до кулі в цій точці.
Вона має з кулею тільки одну спільну
точку. Лінією перетину двох сфер є
коло.
Площа
сфери радіусом R обчислюється
за формулою
Площина,
яка проходить через центр кулі,
називається діаметральною
площиною.
Переріз кулі діаметральною площиною
називається великим
кругом,
а переріз сфери — великим
колом,
або екватором.
Будь-яка
діаметральна площина кулі є її площиною
симетрії. Центр кулі є її центром
симетрії.
Площина,
яка проходить через точку А кульової
поверхні та є перпендикулярною до
радіуса, проведеного в точку А,
називається дотичною
площиною.
Точка А називається точкою
дотику.
Дотична
площина має з кулею тільки одну спільну
точку — точку дотику.
Пряма,
яка належить дотичній до кулі площині
й проходить через точку дотику,
називаєтьсядотичною
до кулі в цій точці.
Вона має з кулею тільки одну спільну
точку. Лінією перетину двох сфер є
коло.
Площа
сфери радіусом R обчислюється
за формулою 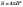 .
Кульовим
сегментом називається
частина кулі, яку відтинає від неї січна
площина.
На
рисунку H —
висота кульового сегмента.
Кульовий
сегмент обмежується частиною сфери,
площа якої обчислюється за формулою
.
Кульовим
сегментом називається
частина кулі, яку відтинає від неї січна
площина.
На
рисунку H —
висота кульового сегмента.
Кульовий
сегмент обмежується частиною сфери,
площа якої обчислюється за формулою  ,
і кругом, який називається основою сегмента.
Кульовий
сектор —
це кульовий сегмент і конус, вершина
якого в центрі кулі, а основою є основа
сегмента.
,
і кругом, який називається основою сегмента.
Кульовий
сектор —
це кульовий сегмент і конус, вершина
якого в центрі кулі, а основою є основа
сегмента.
Об’єм кулі
На
рисунку зображено кулю, кульовий сегмент
і кульовий сектор. Об’єм
кулі:
Об’єм
кулі:
 ,
де R —
радіус кулі.
Об’єм кульового
сегмента:
,
де R —
радіус кулі.
Об’єм кульового
сегмента:
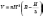 ,
де H —
висота кульового сегмента,
R —
радіус кулі.
Об’єм кульового
сектора:
,
де H —
висота кульового сегмента,
R —
радіус кулі.
Об’єм кульового
сектора:
 ,
де R —
радіус кулі, H —
висота відповідного кульового сегмента.
,
де R —
радіус кулі, H —
висота відповідного кульового сегмента.
