
- •Часть 4. Элементы аналитической механики Глава 1. Основные понятия
- •1.1. Классификация связей
- •1.2. Виртуальные перемещения
- •1.3. Условия, налагаемые связями на вариации координат
- •1.4. Обобщенные координаты, степени свободы
- •1.5. Работа сил на виртуальных перемещениях, идеальные связи, обобщенные силы
- •Глава 2. Аналитическая статика
- •2.1. Принцип виртуальных перемещений
- •2.2. Условия равновесия смт в обобщенных координатах
- •Глава 3. Аналитическая динамика
- •3.1. Общее уравнение динамики – уравнение Даламбера-Лагранжа
- •3.2. Уравнения движения смт в обобщенных координатах – уравнения Лагранжа второго рода
- •Глава 4. Алгоритмы решения задач
- •Пример 1.
- •Пример 2
- •Пример 3
- •Пример 4
- •Пример 5
- •Пример 6.
- •Пример 7
- •Пример 8
Пример 7
2 Используя условие задачи примера 4 (рис. 5), определить ускорение груза и его скорость в зависимости от пройденного им пути с помощью уравнения Лагранжа второго рода.
3 Равновесие объекта: нет, движение объекта.
4
Обобщенная координата:
![]() .
.
Степень свободы:
![]() .
.
5б
Связи стационарные, удерживающие и
неидеальные (работы силы трения скольжения
и момента трения качения на виртуальных
перемещениях не равны нулю). Силовая
схема, состоящая из
![]() представлена на рис. 15.
представлена на рис. 15.
Нормальные реакции
связей
![]() не войдут в обобщенные силы, так как их
работы на виртуальных перемещениях
равны нулю.
не войдут в обобщенные силы, так как их
работы на виртуальных перемещениях
равны нулю.
Сила трения скольжения и момент трения качения условно принимаются за активные силы:
![]() ,
,
![]() .
.
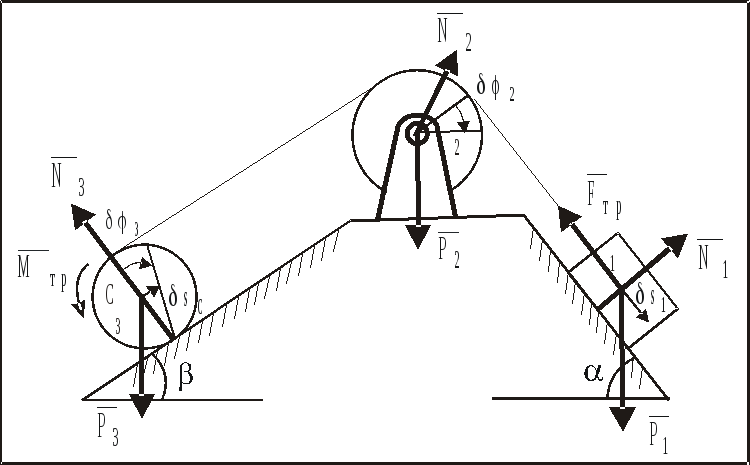
Рис. 15
6



![]() б
Д49 КЭС
3 – 6
б
Д49 КЭС
3 – 6
![]()
![]()
7б
Виртуальные перемещения
![]() изображены на рис. 15.
изображены на рис. 15.
Соотношения между
виртуальными перемещениями выражаются
через
![]() ,
так как степень свободы МС
,
так как степень свободы МС
![]() .
Эти соотношения получены в примере 4
настоящей главы:
.
Эти соотношения получены в примере 4
настоящей главы:
![]() ,
,
![]() ,
,
![]()
8б
Подставив в
![]() полученные в уровне 5б
выражения для силы трения скольжения,
момента трения качения, а также соотношения
между виртуальными перемещениями,
найденные в уровне 6б,
получим:
полученные в уровне 5б
выражения для силы трения скольжения,
момента трения качения, а также соотношения
между виртуальными перемещениями,
найденные в уровне 6б,
получим:
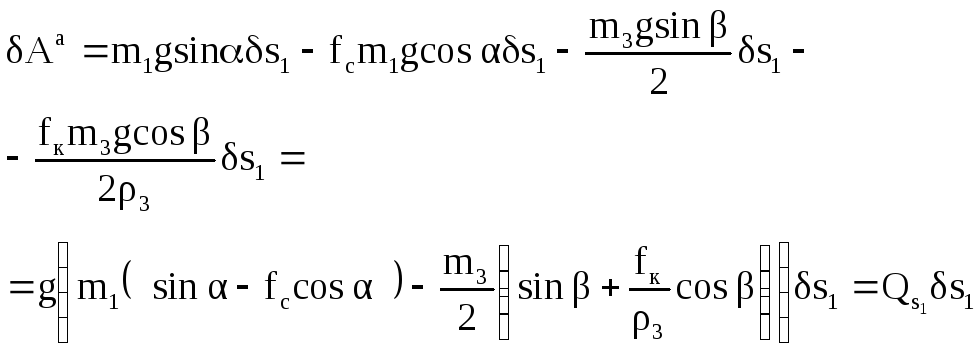
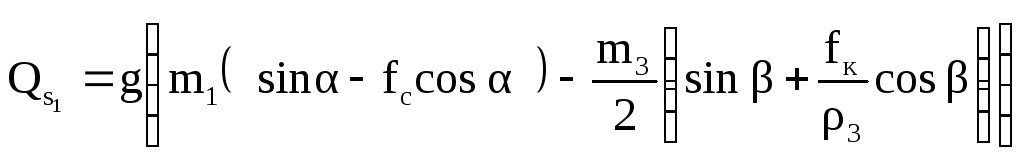 .
.
9
 б
Д49 КЭС
б
Д49 КЭС
Т
Кинетическая энергия МС найдена в примере 1 главы 4, п. 4.9, Ч.3 Динамика (рис. 38).
![]() .
.
10б
![]() ,
,
![]() .
.
11 Составим уравнение Лагранжа второго рода
![]() .
.
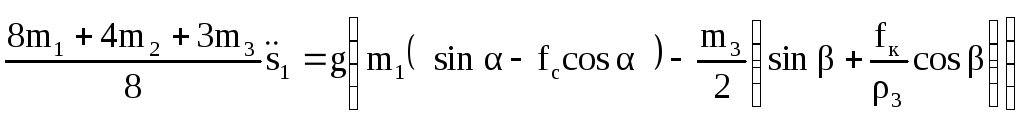
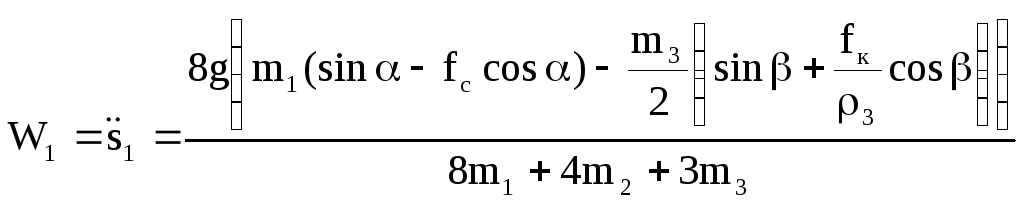 .
.
12 Ответ:
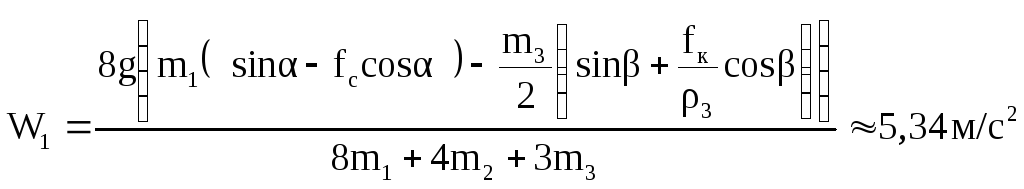 .
.
Скорость груза с учетом нулевых начальных условий можно найти путем искусственного преобразования и интегрирования методом разделения переменных (аналогично тому, как это сделано в примере 4 настоящей главы):
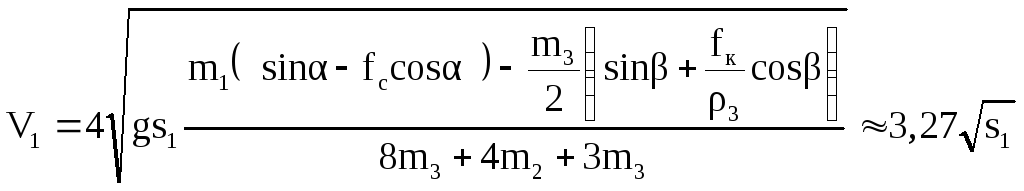
Условия того, чтобы
груз опускался
![]() ,
т.е.
,
т.е.
![]() .
.
Эти условия выполняются, следовательно, груз 1 опускается.
Пример 8
2 Используются условия задачи примера 5 (рис. 6).
Найти системуыражаем
все изображенные на рис.
3 Равновесие объекта: нет, движение объекта.
4б
Обобщенные координаты
![]() .
.
Степень свободы
![]() .
.
5б Связи стационарные, удерживающие и идеальные.
Силовая схема,
состоящая из
![]() ,
представлена на рис. 16. Сила упругости
,
представлена на рис. 16. Сила упругости
![]() .
.
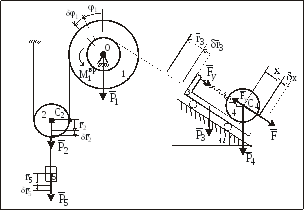
Рис. 16
Р![]() еакции
идеальных связей
еакции
идеальных связей
![]() можно не изображать на рисунке, так как
они не войдут в обобщенные силы.
можно не изображать на рисунке, так как
они не войдут в обобщенные силы.
6


 б
Д49 КЭС
3 – 6
б
Д49 КЭС
3 – 6
![]()
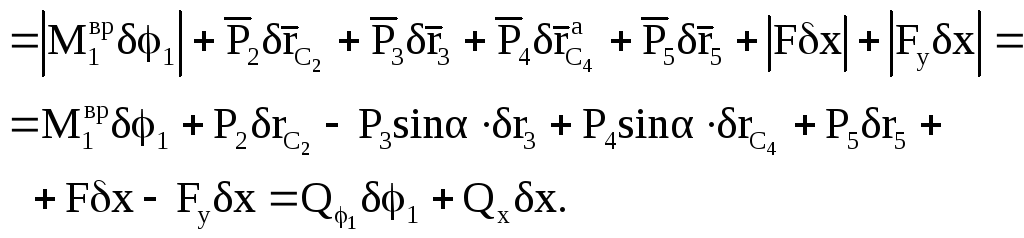
7б
Виртуальные перемещения
![]() ,
,![]() (виртуальное абсолютное перемещение
центра масс катка),
(виртуальное абсолютное перемещение
центра масс катка),
![]() (виртуальное относительное перемещение
центра масс катка),
(виртуальное относительное перемещение
центра масс катка),
![]() изображены на рис. 16.
изображены на рис. 16.
Соотношения между
виртуальными перемещениями выражаются
через
![]() ,
так как степень свободы МС
,
так как степень свободы МС
![]() .
.
Эти соотношения получены в примере 5:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
8б Подставим
в
![]() полученное
в уровне 5б
выражение для силы упругости, а также
соотношения, выражающие зависимость
между виртуальными перемещениями,
найденные в уровне 7б,
получим:
полученное
в уровне 5б
выражение для силы упругости, а также
соотношения, выражающие зависимость
между виртуальными перемещениями,
найденные в уровне 7б,
получим:
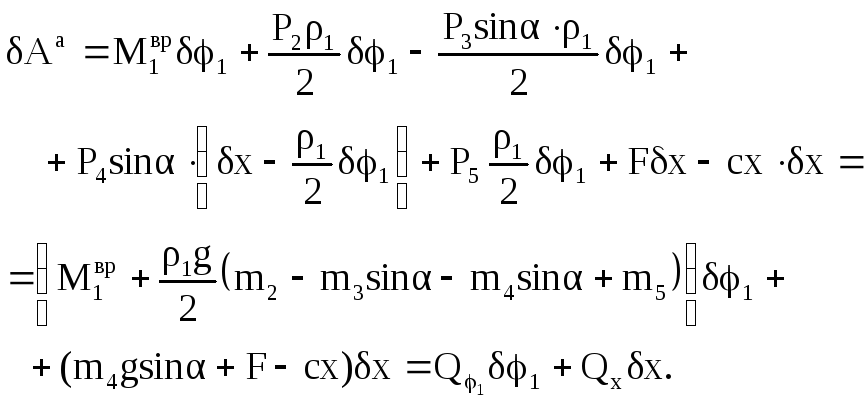
![]()
![]() .
.
9
 б
Д49 КЭС
б
Д49 КЭС
Т
![]()
![]()
8 Неподвижный блок совершает вращательное
движение.
Неподвижный блок совершает вращательное
движение.
9
![]() ,
здесь
,
здесь
![]() .
.
![]()
8 Подвижный блок совершает плоско-параллельное
движение.
Подвижный блок совершает плоско-параллельное
движение.
9
![]() ,
,
здесь
![]() .
.
![]()
8 Тележка совершает поступательное
движение.
Тележка совершает поступательное
движение.
9
![]() ,
здесь
,
здесь
![]() .
.
![]()
8 Каток совершает сложное движение:
поступательное вместе с тележкой
(переносное движение) и плоско-параллельное
относительно тележки (относительное
движение)
Каток совершает сложное движение:
поступательное вместе с тележкой
(переносное движение) и плоско-параллельное
относительно тележки (относительное
движение)
![]() ,
,
здесь
![]() ,
,
![]() ,
,
![]() .
.
![]()
8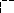 Груз совершает прямолинейное движение
МТ.
Груз совершает прямолинейное движение
МТ.
9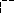
![]() ,
здесь
,
здесь
![]()
1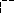 0
0
![]()
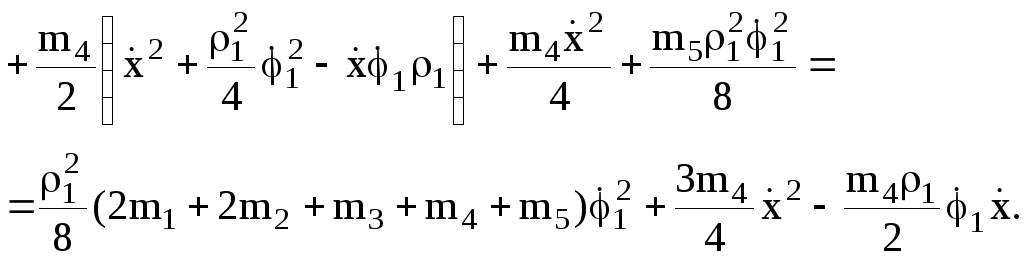
10
Прежде, чем записать уравнения Лагранжа
второго рода, найдем частные производные
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
11 Уравнения Лагранжа второго рода:
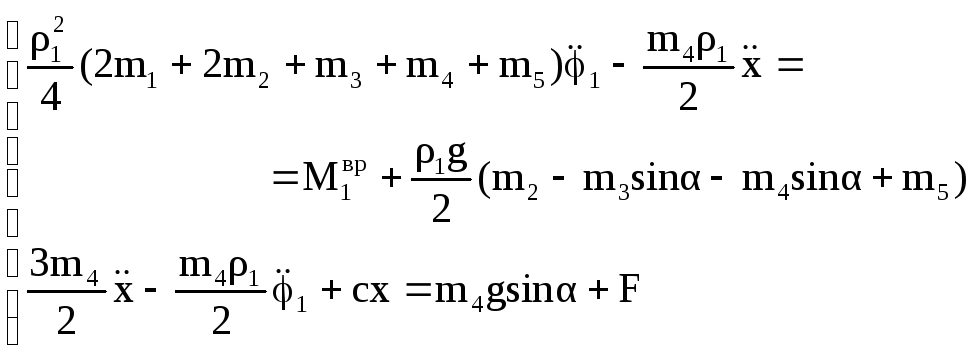
12 Ответ:
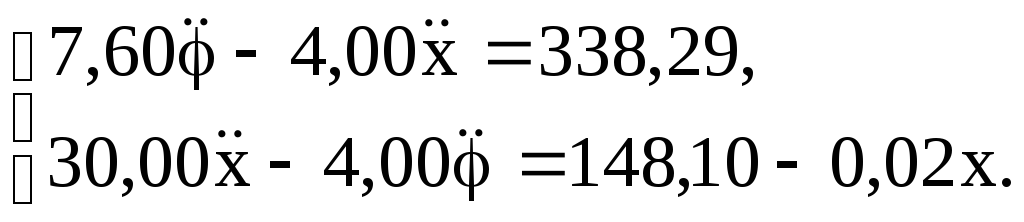
Примечание
Сравнивая решения задач в примерах 4 и 5 с решением задач в примерах 7 и 8, можно сделать вывод, что использование уравнений Лагранжа второго рода по сравнению с общим уравнением динамики дает более универсальный и рациональный метод решения задач динамики.
Заключение
Алгоритм аналитической механики – управляющий
А00 УПР с комментариями
-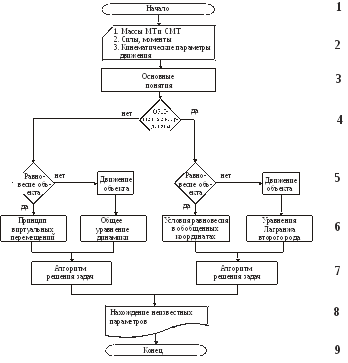
Комментарии
К.3. Вводятся основные понятия аналитической механики: классификация связей, виртуальные перемещения, обобщенные координаты, степени свободы, работа сил на виртуальных перемещениях, обобщенные силы, идеальные связи (глава 1).
К.4,5,6. Используются две формы условий равновесия: СМТ принцип виртуальных перемещений и условия равновесия в обобщенных координатах и два условия движения СМТ: общее уравнение динамики, уравнение движения СМТ в обобщенных координатах – уравнения Лагранжа второго рода (главы 2 и 3).
К.7. Рассматриваются два алгоритма решения задач с комментариями и примерами: один с использованием принципа виртуальных перемещений и общего уравнения динамики, другой с помощью условий равновесия в обобщенных координатах и уравнений движения СМТ в обобщенных координатах – уравнений Лагранжа второго рода (глава 4)
