34. Основные теоремы дифференциального исчисления. Правило Лопиталя.
Ответ: Корнем или нулем функции наз. такое значение аргумента. При котором это функция обращается в нуль
Т. Роля. Между двумя различными корнями дифференцируемой функции содержаться по меньшей мере один корень ее производной
Т. Логранта. Если функция f(x) непрерывна [a,b] то существует такая точка С€(а,b) что f(b)-f(a)=f’(C)(b-a)-формула конечных приращений.
Т.Коши. Если y=f(x) и q=µ(x)- две функции непрерывны на [a, b] и дифференцируемые на интервале (а и в).При исследовании функции может проявится необходимость нахождения предела дроби f(x) и µ(х) числитель и знаменатель которой стремятся к нулю или бесконечность при х→а. Нахождение таких пределов наз. раскрытием неопределённостей соответствующего вида Основа его правила Лопиталя.
Т.
Лопиталя. Если функций f(х)
дефференц. В окрестности точки a
x=a,
обращаются в нуль этой точке и существует
предел
то существует и предемл отношений самых
функций равны пределу отношение
производной.
35. Дифференциация 1-го порядка, его свойства, использование в приближенных вычислениях.
Ответ:
Дифференциалом функции y=f(x)
наз. произведение производной этой
функции
,dx
=
то есть дифференциал независемой
переменной равен приращению dy=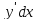
-формула
для вычисления дифференциала. То есть
производная функции равна отношению
данной функции дифференциалу его
аргумента
Свойства
1)dc=0 с-const
2)Дифференциал алгебраической суммы нескольких дифференцируемых функций равен такой же алгебраической сумме дифференциалов слагаемых d(u-v-w)=du-dv+dw
3)Дифференциал произведение двух дифференцируемых функций: d(uv)=udv+vdu
4)Дифференциал
частного
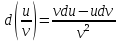
5)Дифференциал сложной функции равен произведению производной первой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента
36. Производные высших порядков. Формула Лейбница. Дифференциалы высших порядков.
Ответ: Производная от производной F(X) наз. производной второго порядка f”(x)=(f’(x))’
В
случае дифференцируемости производной
,
n€
N
производная порядка определяется
равенством.f^(n)(x)=(f^n-1(x))
y=f(x)
f”(x)=(f’(x))’=d^2y/dx^2
f”’(x)=…=d^3y/dx^3
Дифференциал от дифференциала функции y=f(x) наз. дифференциалом 2 порядка
Дифференциалом n порядка наз. дифференциал от дифференциал (n-1)-го порядка.
37. Монотонность и экстремумы функций. Признак монотонности функции. Необходимое и достаточное условие экстремума.
Ответ: Монотонность функции если в данном промежутке производная функции положительная то функция возрастает на этом промежутке если отрицательная то –убывает.
Необходимое условие экстремума. Если экстремума дифференцируемой функции производная равна нулю. Так же функция может достигать экстремума в точке которой производной не существует.
1-ое достаточное условие. Если в точке х=х0 производная функции y=f(х) равна 0 и меняет знак при переходе через точку, то х0-точка экстремума, причем если х0 точка максимума, знак меняется с + на -, а если х0 точка минимума то знак меняется с минуса на плюс
2-ое достаточное условие. Если в точке х=х0 первая производная функции y=f(x) равна нулю, а вторая отлична от нуля то х0 – точка экстремума причем х0 точка минимума ,если f”(x0)>0,х0 точка максимума, если f” (x0)<0
38. Выпуклость и перегиб. Асимптоты графика функции.
Ответ: График функции y=f(x) наз. Выпуклым вниз (вверх ) в данном промежутке если он целиком расположен выше (ниже) касательной в его производной точке.
Признак выпуклости. Если вторая производная функции y=f(x) в данном промежутке положительна (f”(x)>0),то график ее является выпуклым вниз в этом промежутке, а если f”(x) <0, то выпуклый вверх в соответствующем промежутке
Точкой перегиба графика y=f(x) наз. такая его точка M0,в которой меняется направление выпуклости (М0 точка непрерывности функции )
Признак точки перегиба. Если в точке х=х0 2-ая производная функции y=f(x) обращается в нуль (или не существует ) и меняет знак при переходе через нее , то М0 (х0,f(x0)) точка перегиба.
Асимптоты- прямые к которым неограниченно приближается данная линия , когда ее точка неограниченно удаляется от начала координат.