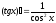Замечание:

Эта теорема неверна, если отрезок [a,b] заменить интервалом (a,b). Например, ƒ(x) - непрерывна на (0,1), но не ограничена так как .

Определение. Наибольшим значением функции y= ƒ(x) на отрезке [a,b] называется такое ее значение ƒ(x), что ƒ(x)≤ ƒ(x₁) при .

Определение. Наименьшим значением функции y= ƒ(x) на отрезке [a,b] называется такое ее значение ƒ(x), что ƒ(x)≥ ƒ(x₁) при .

Теорема 4 (Вторая теорема Вейерштрасса)

Функция, непрерывная на отрезке [a,b], достигает в нем своего наименьшего m и наибольшего M значения, т.е. , , что ƒ(x₁)=m, ƒ(x₂)=M.

Неубывающие и невозрастающие функции называются монотонными.

Возрастающие и убывающие функции называются строго монотонными.

Теорема 5 (О непрерывности обратной функции)

Пусть функция ƒ(x)определена, строго монотонна и непрерывна на некотором промежутке X, и пусть Y – множество ее значений. Тогда на множестве Y обратная функция однозначна, строго монотонна и непрерывна.

Например:

Функция y=sinx на возрастает, непрерывна и множество ее значений – [-1; 1]. По теореме 5 на [-1; 1] существует непрерывная, возрастающая обратная функция со множеством значений : x=arcsiny. Если теперь x и y поменять местами, т.е. рассмотреть функцию y=arcsinx, то получим график:

32. Приращение аргумента, приращение функции. Понятие производной. Физический и геометрический смысл производной.

33. Правила дифференцирования. Таблица производных. Производная сложной функции.

Функция, имеющая производную в данной точке называется дифференцируемой в данной точке.

Функция называется дифференцируемой в данном промежутке, если она имеет производную в каждой точке данного промежутка.

Если промежуток замкнутый, то на концах – односторонняя производная.

Теорема 1 (зависимость между непрерывностью и дифференцированием):

Если функция y=f(x) дифференцируема в данной точке, то она и непрерывна в ней.

Замечание: Обратное не всегда верно.

- в точке x=1 непрерывна, но не дифференцируема.

Пусть f(x) – дифференцируема в точке x, т.е. существует .

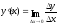Т.к. , то переходя к пределу

Действительно функция непрерывна (по необходимому и достаточному условию непрерывности).

Теорема 2:

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций.

Пусть , где - дифференцируемые функции.

Т.к. ,

переходя к пределу

Таким образом,

Следствие: Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых.

Теорема 3:

Производная двух дифференцируемых функций определяется формулой

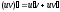
Следствие 1:

Постоянный множитель можно выносить за знак производной.

Следствие 2:

Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на остальные:

Например:

Теорема 4:

Производная частного двух дифференцируемых функций определяется формулой

Рассмотрим сложную функцию , где x – независимая переменная, а - промежуточный аргумент.

Теорема 5:

Если y=f(x) и - дифференцируемые функции своих аргументов, то производная сложной функции существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

или

Например:

Основные формулы дифференцирования: