Свойства функций, непрерывных в точке.

Выражают следующие теоремы:

Теорема1: Если функции f(x) и φ(x) непрерывны в точке х0 , то также непрерывны в этой точке их сумма f(x)+φ(x), разность f(x)-φ(х), произведение 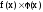и частное при условии .

Т.к. непрерывные в точке х0 функции f(x) и φ(х) имеют в этой точке пределы равные f(x0) и φ(х0), то пределы суммы, разности, произведения, частного существуют и равны соответственно f(x0)+φ(x0), f(x0)-φ(х0), ,.

А эти величины равны значениям соответствующих функций в точке х0, следовательно функции f(x)+φ(x), f(x)-φ(х), , непрерывны в точке х0 .

Следствие1: Целая рациональная функция или непрерывна при любых х.

Следстви2: Дробная рациональная функция:

непрерывна при любых х, для которых знаменатель не равен нулю.

Теорема2: Если функция φ(х) непрерывна в точке х0 , а функция f(x) непрерывна в точке y0 =φ(x0), то сложная функция F(x)=f(φ(x)), непрерывна в точке х0 .

Теорема3: Все основные элементарные функции непрерывны там, где они определены.

1) Найти предел

Решение:

Т.к. функция непрерывна в точке , т.е. 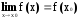, то переходя к пределу получаем:

2)

Решение:

Переходя к предельному значению аргумента, получаем неопределенность вида .

f(x) не определена в точке х=0, т.е. не является непрерывной в этой точке. Значит сразу переходить к пределу нельзя, надо функцию преобразовать так, что бы при х≠0 она совпала с функцией, непрерывной в точке х0. Для этого числитель и знаменатель умножим на выражение сопряженное числителю:

Рассмотрим функцию y=f(x), определенную на интервале (а,в) кроме быть может, точки х0(а,в)

Определение: Точка х0 называется, точкой разрыва данной функции, если в ней функция определена, но не является непрерывной, или не определена в этой точке.

Определение: Если х0- точка разрыва функции f(x) и существуют конечные пределы слева и справа:

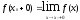, , то она называется точкой разрыва первого рода.

Величина -называется скачком функции в точке х0 .

В точке х0 =0 – разрыв первого рода

В точке х0 =0 f(x)- не определена

Скачок: -2.

Определение: Если функция y=f(x) имеет разрыв в точке х0 и = , тогда х0 называется точка устранимого разрыва.

в точке х0 =0 – устранимый разрыв

В точке х0 =0 функция не определена,

Определение: Если х0 точка разрыва и по крайней мере один из односторонних пределов слева или справа является бесконечным или не существует, то х0 называется точкой разрыва второго рода.

х0 =0 разрыв второго рода

1)

2)

31. Непрерывность функции на отрезке. Теоремы о непрерывностях функций.

Функция называется непрерывной на отрезке [a,b], если она непрерывна в каждой его точке (в точке a непрерывна справа, в точке b слева).

Если функция определена в точке x=a и при этом предел

ƒ(x)=ƒ(a), то функция непрерывна справа, аналогично если

ƒ(x)=ƒ(a), то непрерывна слева.

Теорема 1 (Первая теорема Коши)

Пусть функция ƒ(x) непрерывна на отрезке [a,b] и на концах отрезка имеет значения разных знаков, тогда существует точка в которой ƒ(с)=0.

Теорема 2 (Вторая теорема Коши)

Пусть функция ƒ(x) непрерывна на отрезке [a,b], причем ƒ(a)=A, ƒ(b)=B, где A≠B. Тогда какое бы ни было число С, заключенное между А и B, найдется такая точка , что ƒ(с)=С.

Определение. Функция называется ограниченной на отрезке [a,b] если существует число M>0 такое, что для выполняется неравенство | ƒ(x)≤M|.

Теорема 3 (Первая теорема Вейерштрасса)

Если функция ƒ(x) определена и непрерывна на отрезке [a,b], то она ограничена на этом отрезке.