Конверсия рент

55. Сформулируйте принцип финансовой эквивалентности для различных видов конверсии рент

Принцип финансовой эквивалентности заключается в том, что при необходимости изменить условия выплаты ренты, заменить одну ренту другой либо разовым платежом, либо, наоборот, заменить разовый платеж рентой, а также заменить несколько рент с разными параметрами одной, производится конверсия рент, подчиняющихся правилу: современные величины старой и новой рент должны быть равны. Это следует из предположения, что конверсия рент не должна менять финансового положения сторон.

56. Замените годовую ренту с параметрами p–срочной рентой с параметрами .

Приведенная величина годовой ренты

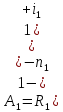
Приведенная величина р-срочной ренты к=1 ;

A₁=A₂

;

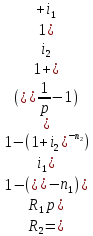
57. Дайте определение и приведите пример выкупа ренты.

Выкуп ренты - замена ренты единовременным платежом. Принцип финансовой эквивалентности здесь сводится к тому, что единовременный платеж P должен равняться современной величине выкупаемой ренты A:

Пример: Заменить p-срочную ренту с параметрами ; ; единовременным платежом в момент времени t=4.

Единовременный платеж в момент t=0:

t=4

58. Дайте определение и приведите пример консолидации рент.

Консолидация рент - объединение нескольких рент в одну, основанное на принципе финансовой эквивалентности. При замене нескольких рент одной равенство современных величин старых и новых рент имеет вид:

это равенство позволяет найти только один параметр консолидирующей ренты (член ренты или срок), при этом все остальные ее параметры должны быть заданы. В случае если неизвестен член ренты, то он для ренты постнумерандо со сроком n определяется:

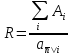
Если же известен срок консолидирующей ренты, то сначала находим коэффициент приведения:

Откуда находим срок рент

Важным частным случаем консолидации рент является ситуация, когда член консолидирующей ренты равен сумме членов заменяемых рент. При одинаковой процентной ставке всех рент из условия финансовой эквивалентности получаем:

Пример: Заменить 2 ренты постнумерандо с параметрами:

; ; ; ;

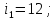
Разовым платежом в момент времени n=4, t=15%

A=, эта сумма должна равняться единовременному платежу, дисконтированному к начальному моменту времени:

Отсюда P = P = 1579,64*

59. Дайте определение и приведите пример рассрочки платежа.

Рассрочкой платежа называется замена долга (единовременного платежа) рентой. При этом задаются все параметры, кроме одного, а этот неизвестный параметр определяется из условия равенства долга современной величине вводимой ренты:

Пример: Заменить единовременный платеж 345000р.в момент времени t=2 p-срочной рентой постнумерандо с параметром ; ;

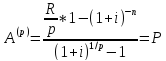
Доходность актива

60. Выразите доходность актива за два периода через доходности актива за каждый из периодов.

Два периода и , стоимость актива в моменты времени и 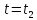обозначим через , имеем:

Доходность за период равна: t=+

перемножив два выражения имеем:

=>

61. Выразите доходность актива за три периода в целом через доходность актива за каждый из периодов.

Три периода 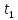, ,, стоимость актива в моменты времени обозначим через , имеем:

Доходность за период равна: t=+ +

=>

=>

=>

62. Выразите доходность актива за несколько периодов в целом через доходность актива за каждый из периодов (используйте метод математической индукции).

Найдём доходность за несколько периодов, если доходность за каждый период известна. Пусть доходности за последовательные периоды времени t₁, t₂, … , t_n равны и µ₁, µ₂, …, µ_n соответственно.

Доходность за несколько периодов

Тогда доходность µ за период t=t₁+t₂+…+t_n выражается формулой

µ=(µ₁+1)*(µ₂+1)*…*(µ_n+1)-1.

Для равных доходностей за отдельные периоды µ₁=µ₂=…=µ_n (при этом промежутки времени могут оставаться произвольными и не равными друг другу) имеем

µ=(µ₁+1)ⁿ – 1