34. Вывести формулы для приведенной и наращенной величины р–срочной ренты пренумерандо.

По сравнению с рентой постнумерандо начисления на каждый член ренты (за исключением последнего) выше в (1+i) раз за счет начислений за первый период. Наращенная величина р-срочной ренты - рента представляет собой геометрическую прогрессию с первым членом R/p и знаменателем (1+i)^1/p:

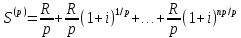
Поэтому наращенная сумма ренты пренумерандо S равна сумме постнумерандо 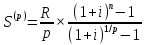умноженной на (1+i):

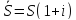
Аналогично для приведенной величины:

Пусть проценты начисляются k раз в году и k=1. Приведенная величина ренты постнумерандо будет 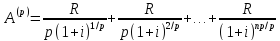и равна сумме геометрической прогрессии с a₁=R/p, q=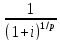 и nnp :

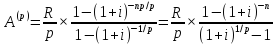
Затем умножив на (1+i) получаем:

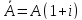
35. Найдите приведенную величину и наращенную сумму p–срочной ренты постнумерандо (случай ).

Число членов ренты равно np, платежи по R/p каждый, начисление процентов k раз в году. Наращенная величина р-срочной ренты равна сумме геометрической прогрессии с первым членом R/p и знаменателем (1+i/k)^k/p:

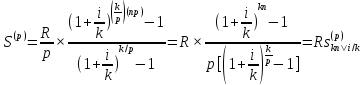
Для приведенной стоимости:

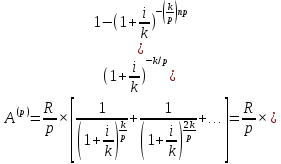
36. Найдите приведенную величину и наращенную сумму p–срочной ренты пренумерандо (случай ).

Для приведенной стоимости р- срочной ренты имеем:

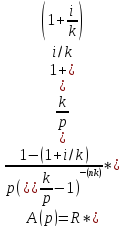
Для наращенной величины ренты имеем:

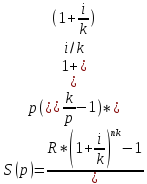
37. Найдите приведенную величину и наращенную сумму p–срочной ренты пренумерандо (случай k = p).

Число членов ренты равно числу начислений процентов, платежи по R/k каждый.

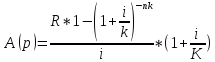
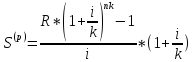
38. Найдите приведенную величину и наращенную сумму p–срочной ренты постнумерандо (случай k = p).

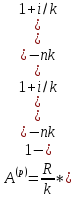
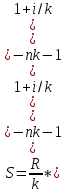
39. Установите связь между приведенной и наращенной величинами p–срочной ренты с непрерывным начислением процентов.

Приведенная величина p–срочной ренты с непрерывным начислением процентов:

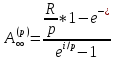
Наращенная величина p–срочной ренты с непрерывным начислением процентов:

Связь между приведенной и наращенной величинами p-срочной ренты с непрерывным начислением процентов имеет вид:

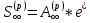
Отсюда получаем выражение для наращенной величины р-срочной ренты с непрерывным начислением процентов

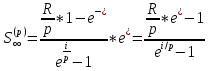
40. Установите связь между приведенной и наращенной величинами p–срочной ренты с k – кратным () начислением процентов.

Связь легко получается из формул приведенной и наращенной величинами p–срочной ренты с k – кратным () начислением процентов:

,

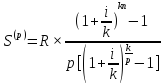
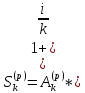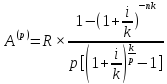
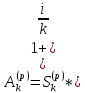
41. Установите связь между приведенной и наращенной величинами p–срочной ренты с k – кратным (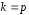) начислением процентов.

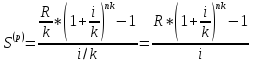
S^(p)=A^(p)* (1+i/p)^np

A^(p) = S^(p) * (1+i/p)^-np

42. От каких параметров ренты зависит связь между приведенной и наращенной величинами ренты.

Коэффициент связи зависит только от кратности начисления процентов и не зависит от срочности ренты и любых других ее параметров. Таким образом,

При однократном начислении процентов

S= A* 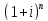, A=S*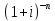

При k-кратном начислении ничислении процентов

S=A* (1+i/k)^kn, A=S*(1+i/k)^-kn

При непрерывном начислении процентов

S=A*eⁿⁱ, A=S*eⁿⁱ

43. Во сколько раз больше будет наращенная сумма в конце n–ого периода при ежепериодном (в конце периода) платеже R, чем при разовом платеже R в начальный момент времени?

Наращенная сумма в конце n-ого периода при платежах R в конце периода равна:

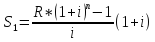
Наращенная сумма в конце n-ого периода при разовом платеже R в начальный момент времени равна:

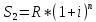
Искомое отношение 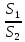равно:

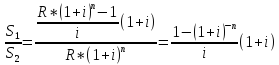
44. Выведите формулы для коэффициентов приведения и наращения 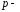срочной ренты постнумерандо с непрерывным начислением процентов.

A_k^(p)=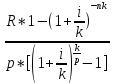, и переходя к пределу при k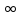, получим из приведенной величины ренты

=*

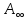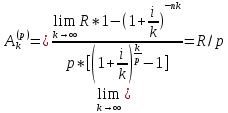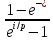
Покажем, что связь между приведенной и наращенной величинами ренты с непрерывным начислением процентов имеет вид:

=

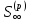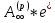
Отсюда получаем выражение для наращенной величины р-срочной ренты с непрерывным начислением процентов

=

=

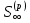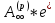
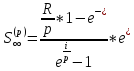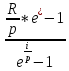
Следовательно,

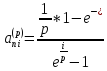
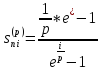
45. Дайте определение непрерывной ренты и выведите формулы для ее коэффициентов приведения и наращения.

Непрерывная рента – рента, при которой рентные платежи производятся непрерывно (через малые промежутки времени).

Переходя к пределу при 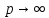, получим непрерывный поток платежей с постоянной плотностью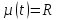 - непрерывную ренту

Найдем предел А^(р) =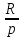* 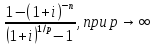. Используя правило Лопиталя, вычислим предел

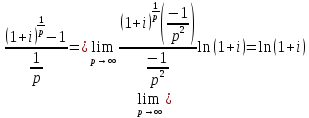
Используя его, получим выражение для приведенной величины непрерывной ренты

^=*

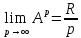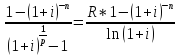
Коэффициент приведения равен

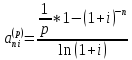
Наращенная сумма непрерывной ренты

S=R*

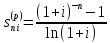
46. Найдите приведенную величину и наращенную сумму непрерывной ренты с k–кратным начислением процентов.

Для приведенной величины:

A_{, k}=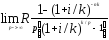

Применим правило Лапиталя и получим:

const

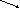
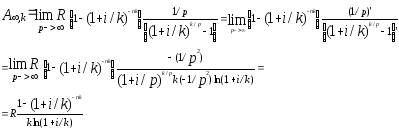
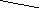
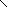
Для наращенной величины:

S_{, k}=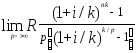

Применим правило Лапиталя для нахождения предела

const

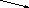
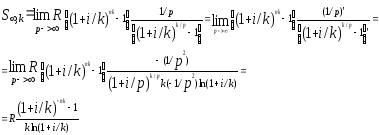
47. Найдите связь между приведенной величиной и наращенной суммой ренты постнумерандо.

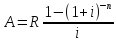
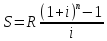
Домножим обе части уравнения 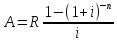на (1+i)ⁿ, тогда получим:

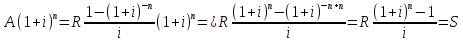
Следовательно

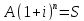
48. Найдите связь между приведенной величиной и наращенной суммой ренты пренумерандо.

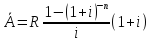
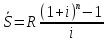(1+i)

Домножим обе части уравнения 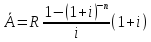на (1+i)ⁿ, тогда получим:

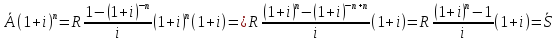
Следовательно

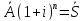
49. Найдите связь между приведенной величиной и наращенной суммой ренты постнумерандо с ежеквартальным начислением процентов.

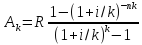
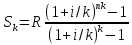
при k=4 получим:

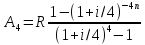
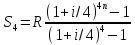
Домножим обе части уравнения 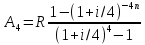на (1+i/4)⁴ⁿ, тогда получим:

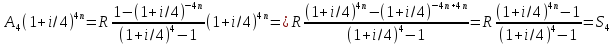
Следовательно

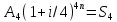
50. Найдите связь между приведенной величиной и наращенной суммой ренты пренумерандо с ежемесячным начислением процентов.

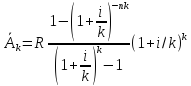
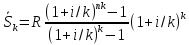
при k=12 получим:

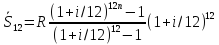
Домножим обе части уравнения 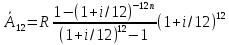на (1+i/12)¹²ⁿ, тогда получим:

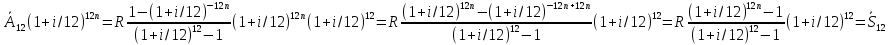
Следовательно

51. Найдите связь между приведенной величиной и наращенной суммой p–срочной ренты постнумерандо с ежемесячным начислением процентов.

Приведенная величина

Наращенная величина

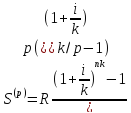
Так как % начисляются ежемесячно, то к=12

Найдем связь между S_p,12 и A_p,12. Домножим на (1+i/k)^kn, получим

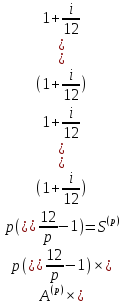
53. Найдите связь между приведенной величиной и наращенной суммой непрерывной ренты с непрерывным начислением процентов.

Приведенная непрерывная величина с непрерывным начислением %

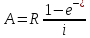
Наращенная непрерывная величина с непрерывным начислением % 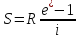, Домножим приведенную величину A на eⁿⁱ, получим

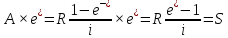
54. Во сколько раз увеличится приведенная величина ренты постнумерандо, если платежи производить в начале периода?

Приведенная величина ренты постнумерандо

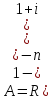
Приведенная величина ренты пренумерандо

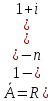
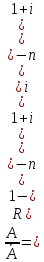
Приведенная величина ренты постнумерандо, при платежах в начале периода в 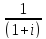раз.