Расчет параметров ренты

25. Пусть известны n, i, R. Найдите наращенную сумму S и приведенную величину A годовой ренты.

Рента постнумерандо:

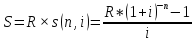
Рента пренумерандо:

26. Пусть известны A, i, R. Найдите срок ренты n.

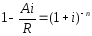
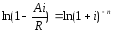
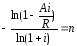
27. Пусть известны S, i, R. Найдите срок ренты n.

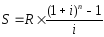
28. Пусть известны n, i, A. Найдите рентный платеж .

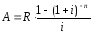
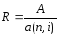
Пусть известны n, i, S. Найдите рентный платеж .

28*.Пусть известны n, i, S. Найти рентный платеж R.

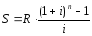
29. Пусть заданы n, R, A. Найдите процентную ставку i .

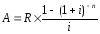
Не решается аналитически, можно решить только приближенно. Для нахождения процентной ставки i можно использовать линейное приближение либо итерационный метод(метод подбора значений). В линейном приближении зная R и А сначала находим коэффициент приведения: .

Далее находим процентную ставку i по интерполяционной формуле:

,

где a₁ и а₂ – значения коэффициента приведения при минимальной и максимальной процентной ставке (i₁ и i₂ соответственно);

а - значение коэффициента приведения при искомой процентной ставке i.

30. Пусть заданы n, r, s. Найдите процентную ставку I .

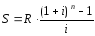
Не решается аналитически, можно решить только приближенно. Для нахождения процентной ставки i можно использовать линейное приближение либо итерационный метод (метод подбора значений). В линейном приближении зная R и S сначала находим коэффициент наращения: 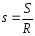. Далее находим процентную ставку i по интерполяционной формуле:

,

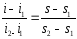где s₁ и s₂ – значения коэффициента наращения при минимальной и максимальной процентной ставке (i₁ и i₂ соответственно);

s - значение коэффициента наращения при искомой процентной ставке i.

31. Найдите приведенную величину и наращенную сумму вечной ренты.

Пусть есть вечная рента {(0, 0), (R, 1), (R, 2)…}. Сумма бесконечно убывающей геометрической прогрессии: 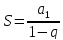c и 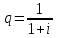получаем

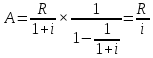– это приведенная стоимость.

Таким образом, R=Ai, что значит «заплатив сумму A, владелец вечной ренты получает право на получение рентных платежей, равных процентам на сумму А. Наращенная величина вечной ренты и коэффициент наращения равны бесконечности. Для последнего:

32. Для бессрочной (вечной) ренты определить, что больше увеличит приведенную стоимость этой ренты; увели­чение рентного платежа на 2% или уменьшение процентной ставки на 2%?

Приведенная стоимость вечной ренты равна

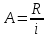
При увеличении рентного платежа на 2% R заменяется на 1,02R и приведенная величина ренты становится

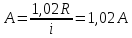
При уменьшении процентной ставки на 2% i заменяется на 0,98i и приведенная стоимость ренты становится 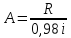= 1,0204А

Во втором случае приведенная стоимость ренты больше, следовательно, уменьшение процентной ставки на 2% больше увеличивает приведенную стоимость вечной ренты, чем увеличение рентного платежа на 2%.

33. Вывести формулы для приведенной и наращенной величины р–срочной ренты постнумерандо.

Когда рентный платеж R производится не единовременно, а разбит на p одинаковых платежей, равномерно распределенных в течение года, то соответствующий поток платежей имеет вид:

CF={(R/p, 1/p), (R/p, 2/p), …, (R/p, (n-1)/p), (R/p, n)}

И называется р-срочной рентой.

Пусть проценты начисляются k раз в году и k=1. Приведенная величина ренты постнумерандо будет и равна сумме геометрической прогрессии с a₁=R/p, q=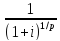 и nnp :

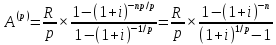
Наращенная величина р-срочной ренты. Рента представляет собой геометрическую прогрессию с первым членом R/p и знаменателем (1+i)^1/p:

Находим ее сумму: . Это величина.

А s_n|i^(p) = - коэффициент наращения р-срочной ренты.