18. Найти хроматическое число заданного графа, используя алгоритм с возвратом для нахождения независимых множеств вершин, указать, какие вершины в какой цвет окрашиваются.

19. Найти хроматический класс заданного графа, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа, указать, какие ребра в какой цвет окрашиваются.

3. Паросочетания

Не менее важным, чем понятие вершинной независимости, является понятие реберной независимости.

Произвольное подмножество попарно несмежных ребер графа называется паросочетанием ( или независимым множеством ребер).

В качестве иллюстрации рассмотрим граф, изображенный на рис.2. В нем паросочетаниями являются, например, х₁,х₃,х₅,х₇, х₁, х₂, х₂,х₆.

х₁ х₂ х₃ х₄ х₅ х₆ х₇

Рис. 3.

Паросочетание графа G называется максимальным, если оно не содержится в паросочетании с большим числом ребер, и наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа G.

Число ребер в наибольшем паросочетании графа G называется числом паросочетания и обозначается ₁(G).

Независимые множества ребер графа G находятся во взаимно однозначном соответствии с независимыми множествами вершин реберного графа L(G)=(V₁,X₁), который для графа G=(V,X) определяется следующими двумя условиями:

1. V₁ = X,

2. вершины х₁ и х₂ смежны в L(G) тогда и только тогда, когда ребра х₁ и х₂ смежны в G.

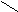
Рис. 4

На рис. 4 изображены два графа – G и L(G). Вершины графа G – темные кружки, вершины графа L(G) – светлые кружки. Ребра графа G – тонкие линии, ребра графа L(G) – жирные линии.

20. Найти все максимальные паросочетания в заданном графе, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа.

21. Найти наибольшее паросочетание в заданном графе, используя алгоритм с возвратом для нахождения независимых множеств вершин реберного графа.

3. Потоки в сетях и родственные задачи

1. Потоки в сетях

1. Полный поток в транспортной сети

Теория транспортных сетей возникла при решении задач, связанных с организацией перевозки грузов. Тем не менее понятие потока на транспортной сети, алгоритм нахождения потока наибольшей величины и критерий существования потока, насыщающего выходные дуги сети, оказались полезными для многих других прикладных и теоретических вопросов комбинаторного характера.

Введем основные понятия данной теории.

Транспортной сетью называется орграф D = (V,X) с множеством вершин V = {v₁,…,v_n}, для которого выполняются условия:

1. существует одна и только одна вершина v₁, называемая источником, такая, что Г^-1 (v₁) =  (т.е. ни одна дуга не заходит в v₁),

2. существует одна и только одна вершина v_n, называемая стоком, такая, что Г(v_n) =  (т.е. из v_n не исходит ни одной дуги),

3. каждой дуге xX поставлено в соответствие целое число c (x)  0, называемое пропускной способностью дуги.

Функция (x), определенная на множестве X дуг транспортной сети D и принимающая целочисленные значения, называется допустимым потоком (или просто потоком) в транспортной сети D, если

1. для любой дуги xX величина (x), называемая потоком по дуге x, удовлетворяет условию 0  (x)  c(x),

2. для любой промежуточной вершины v сумма потоков по дугам, заходящим в v, равна сумме потоков по дугам, исходящим из v.

Величиной потока  в транспортной сети D называется величина, равная сумме потоков по всем дугам, заходящим в сток, или, что то же самое сумме потоков по всем дугам, исходящим из источника.

Дуга xX называется насыщенной, если поток по ней равен ее пропускной способности. Поток  называется полным, если любой путь в сети из источника в сток содержит, по крайней мере, одну насыщенную дугу.

А л г о р и т м