6. Метод Свенна для поиска отрезка, содержащего точку минимума

М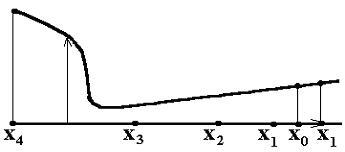етод Свенна – это эвристический метод, который определяет интервал неопределенности, содержащий точку минимума. Пусть требуется найти минимум функции f(x) не на отрезке, а на всей оси х. Берем функцию f(x), которая унимодальна. Выберем некоторое начальное приближение x0 и сделаем из него шаг некоторой длины h: x1 = x0 + h. Если f(x1)>f(x0), то изменим направление шага и положим x1= x0 + h. Пусть теперь f(x1 )<f(x0 ). Далее удвоим шаг h' = 2h и положим x2=x1 + h ' и т.д., до тех пор, пока на некотором шаге не будет выполнено условие f(x_n)<f(x_n-1). В рассматриваемом примере f(x4)>f(x3), следовательно минимум унимодальной функции лежит на отрезке [x4,x3] и его можно найти одним из методов, основанном на уменьшении интервала(метод общего поиска, деления отрезка пополам, золотого сечения).

Главное достоинство методов поиска отрезка, содержащего точку минимума состоит в том, что они основаны на вычислении только значений функции и, следовательно, не требуют вычисления производных. Но также есть и недостаток - скорость их сходимости невелика. Метод Свенна только значения функции f(x). Этот метод называется методом 0-го порядка.

7. Одномерная оптимизация. Метод Ньютона-Рафсона

Рассмотрим функцию f(x). Если предположить, что функция f(x) дифференцируема, то существуют методы, использующие производные. Методы, использующие вторую производную, называются методами 2-го порядка. Пусть f(x) дважды дифференцируема. Необходимым условием min функции является =0, где x*- минимум функции. А чтобы x* было именно min достаточно выполнения условия >0. Будем решать уравнение =0. Зададим некоторое начальное приближение x_k, построим квадратическую модель функции с помощью разложения в этой точки функции в ряд Тейлора. Получаем:

Если , то будет иметь единственную стационарную точку. Найти ее можно, для чего приравняем :.

Решим это уравнение относительно х и полученное решение запишем в виде x_k+1, как очередное приближение к min, т.е.

(*). Функцию (*) можно получить по-другому, если применить метод касательной, т.е. численный метод нахождения 0 функции g(0) =0, а g(x)=, тогда . Рассмотренный метод обычно называют методом Ньютона/ Ньютона – Рафсона.

Однако у метода есть недостатки: 1.Уравнение =0 может определить не только min, но и max.

2.Модельная функцияможет сильно отличаться от оптимизируемойи шаг

может оказаться слишком большим:

Поэтому, чтобы избежать такого случая, будем на каждом шаге проверять соотношения

<, если оно выполняется, то переходим к следующему шагу и т.д. Если же >, а < 0, то должна первоначально уменьшится в направлении от к (это следует из квадратичной модели). Поэтому следующую точку можно найти, дробя шаг в обратном направлении, например, положив . Из основной формулы метода видно, что выражение отрицательное тогда и только тогда, когда > 0. Это гарантия существования подходящего направления шага, направленного в сторону минимума. С другой стороны, если<0 и >0, то первоначально увеличивается, поэтому шаг нужно сделать в противоположном направлении. Критерии останова для данного метода <ε, где ε - заданная точность.