14. Задачи с ограничениями. Поиск оптимума в задачах с ограничениями типа равенств. Метод неопределенных множителей Лагранжа.

Рассмотрим задачу:

при ограничениях . Решением такой задачи является метод множителей Лагранжа.

С помощью данного метода устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями-равенствами. При этом задача с ограничениями преобразуется в эквивалентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Лагранжа. Рассмотрим более конкретную задачу с одним ограничением-равенством: , ограничение: .

В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной минимизации:

Функция называется функцией Лагранжа. Здесь – множитель Лагранжа.

Пусть при заданном значении безусловный минимум функции по переменной х достигается в точке и удовлетворяет уравнению .

Тогда, как не трудно видеть, минимизирует начальную функцию с учетом ограничения.

Также нужно подобрать значение таким образом, чтобы координата точки безусловного минимума удовлетворяла равенству-ограничению. Это можно сделать, если, рассматривая как переменную, найти безусловный минимум функции Лагранжа в виде функции , а затем выбрать значение , при котором выполняется равенство основной функции.

Очень часто оказывается, что решение системы 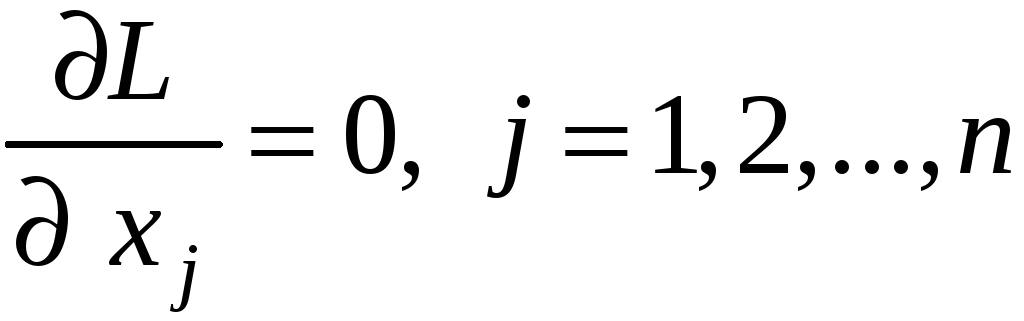в виде явной функции переменной получить нельзя. Тогда значения и находятся путем решения следующей системы, состоящей из n+1 уравнений с n+1 неизвестными:

Решить такую систему можно решить каким-либо численным методом. Для каждого из решений вычисляется матрица Гессе функции Лагранжа, рассматриваемой как функция от . Если она положительно определена, то решение – точка минимума.

Метод множителей Лагранжа можно распространить на случай, когда задача имеет несколько ограничений в виде равенств: , .

Функция Лагранжа принимает вид .

Здесь – множители Лагранжа, то есть неизвестные параметры, значения которых нужно определить. Приравнивая частные производные L по нулю, получаем следующую систему.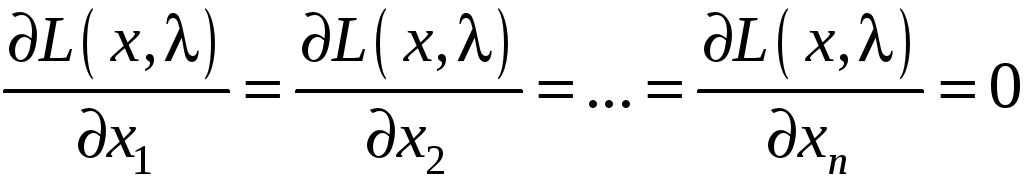

Если найти решение этой системы в виде функций от вектора затруднительно, то можно расширить последнюю систему путем включения в неё ограничений-равенств:

. Решение расширенной системы, состоящей из N+K уравнений с N+K неизвестными, определяет стационарную точку функции L. Затем реализуется процедура проверки на минимум или максимум, которая проводится на основе вычисления элементов матрицы Гессе функции Лагранжа, рассматриваемой как функция от x.

15. Поиск оптимума в задачах с ограничениями. Методы штрафных и барьерных функций.

Методы штрафных функций

Рассмотрим задачу условной оптимизации или нелинейного программирования , которая имеет ограничения: , ,. ( Говорят, что точка x соответствует допустимому решению задачи нелинейного программирования, если для нее выполняются все ограничения. Предполагается, что для вектора x^*, являющегося решением задачи нелинейного программирования, известно некоторое начальное приближение x⁰ , возможно недопустимое. В методах штрафных функция строится последовательность точек x^m, m=0,1,...,M, которая начинается с заданной точки x⁰ и заканчивается точкой x^M, дающая наилучшее приближение к x^* среди всех точек построенной последовательности. В качестве x^m берутся точки решения вспомогательной задачи безусловной минимизации, полученной с помощью преобразования исходной целевой функции с помощью штрафных функций. В этих методах исходная задача условной оптимизации преобразуется в последовательность задач безусловной оптимизации.

Методы штрафных функций классифицируются в соответствии со способами учета ограничений-неравенств. В зависимости от того, являются ли элементы последовательности x^m допустимыми или недопустимыми точками, говорят о методах внутренней и внешней точки соответственно. Если последовательность x^m содержит точки обоих типов, метод называют смешанным. Основная идея метода штрафных функций заключается в следующем. Строят вспомогательную функцию , такую, что приближенное решение основной задачи получается в результате решения последовательности задач безусловной минимизации функции . В методе внешних штрафных функций функции H, G выбираются таким образом, чтобы они становились отличными от нуля (положительными) при нарушении соответствующего ограничения. А так как мы минимизируем вспомогательную функцию, то движение в сторону нарушения становится невыгодным. Внутри допустимой области в данном методе функции H и G должны быть равны нулю. Например, для ограничений неравенств G_j(g_i(x))→0, при g_i(x))→0⁺ . Приближенное решение задачи получается в результате решения последовательности задач минимизации вспомогательной функции при r_j,l_k→∞,j=1,...,J, k=1,...,K. Соответствующие методы называют методами внешней точки.

Метод барьерных функций

В методе барьерных функций функции H, G выбираются отличными от нуля в допустимой области и такими, чтобы при приближении к границе допустимой области (изнутри) они возрастали, препятствуя выходу при поиске за границу области. В этом случае эти функции должны быть малыми (положительными или отрицательными) внутри допустимой области и большими положительными вблизи границы (внутри области). Например, для ограничений неравенств , G_j(g_i(x))→∞, при g_i(x))→0^-. Такие методы называют еще методами внутренней точки. В алгоритмах, использующих функции штрафа данного типа, требуют, чтобы в процессе поиска точка x всегда оставалась внутренней точкой допустимой области. Приближенное решение поставленной задачи получается в результате решения последовательности задач минимизации при r_j,l_k→∞,j=1,...,J, k=1,...,K. Для ограничений-равенств при выборе функций штрафов обычно требуют, чтобы H_k(h_k(x))→0 , при h_k(x)→0.

Существуют разного рода функции штрафов, н-р: пропорциональный, логарифмический, квадратичный и т.п.

Последовательность действий при реализации методов штрафных функций или барьерных функций выглядит следующим образом: 1. На основании задачи (5.4-5.7) строим функцию (5.8). Выбираем начальной приближение x и начальные значения коэффициентов штрафа r_j,l_k, число итераций, точность безусловной оптимизации, точность соблюдения ограничений и т.д. 2. Решаем задачу минимизации вспомогательной функции. 3. Если полученное решение не удовлетворяет системе ограничений в случае использования метода штрафных функций, то увеличиваем значения коэффициентов штрафа и снова решаем эту задачу. В случае метода барьерных функций значения коэффициентов уменьшаются, чтобы можно было получить решение на границе. 4. Процесс прекращается, если найденное решение удовлетворяет системе ограничений с определенной точностью.