8. Одномерная оптимизация. Квазиньютоновский метод.

Для нахождения минимума функции f(x) используют модифицированный метод Ньютона – квазиньютоновский метод. Этот метод не использует вычисления производных, все действия выполняются с помощью вычисления функции. Производные находят с помощью аппроксимации. Для начала выберем начальное приближение и малый шаг h. Будем изначально рассматривать три точки . Аппроксимируем производные:

, а вторая производная, следовательно, равна:

.

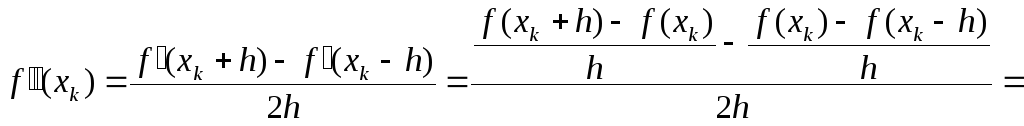
В простом методе Ньютона следующее приближение находиться по формуле: . Подставим значение производных в формулу и получим новое приближение с помощью квазиньютоновского метода:

.

Метод имеет такие же недостатки: 1.Уравнение =0 может определить не только min, но и max.

2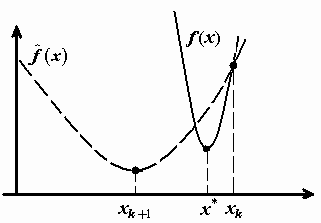.Модельная функцияможет сильно отличаться от оптимизируемойи шаг

может оказаться слишком большим:

Поэтому, чтобы избежать такого случая, будем на каждом шаге проверять соотношения

<, если оно выполняется, то переходим к следующему шагу и т.д. Если же >, а < 0, то должна первоначально уменьшится в направлении от к (это следует из квадратичной модели). Поэтому следующую точку можно найти, дробя шаг в обратном направлении, например, положив . Из основной формулы метода видно, что выражение отрицательное тогда и только тогда, когда > 0. Это гарантия существования подходящего направления шага, направленного в сторону минимума. С другой стороны, если<0 и >0, то первоначально увеличивается, поэтому шаг нужно сделать в противоположном направлении. Критерии останова для данного метода <ε, где ε - заданная точность.

9. Многомерная оптимизация. Рельеф функции. Метод покоординатного спуска.

Изложим этот метод на примере функций трех переменных F(x, y, z). Выберем нулевое приближение, x₀, y₀, z₀. Фиксируем значение двух координат y=y₀, z=z₀. Тогда функция будет зависеть только от одной переменной x; обозначим ее через f₁(x)=F(x, y₀, z₀). Используя какой-либо способ нахождения минимума функции одной переменной, отыщем минимум функции f₁(x) и обозначим его через x₁. Мы сделали шаг из точки (x₀, y₀, z₀) в точку (x₁, y₀, z₀) по направлению, параллельному оси x; значение функции на этом шаге уменьшилось. Теперь из новой точки сделаем спуск по направлению, параллельному оси y, то есть рассмотрим функцию f₂(y)=F(x₁, y₀, z₀), найдем ее минимум и обозначим его через y₁. Второй шаг приводит нас в точку (x₁, y₁, z₀). Из этой точки делаем третий шаг – спуск параллельно оси z и находим минимум функции f₃(z)=F(x₁, y₁, z₀). Приход в точку (x₁, y₁, z₁) завершает цикл спусков или первую итерацию. Далее будем повторять циклы. На каждом спуске функция не возрастает, и при этом значение функции ограничено снизу ее значением в минимуме F^*=F(x^*, y^*, z^*). Следовательно, итерации сходятся к некоторому пределу . Будет ли здесь иметь место равенство, то есть, сойдутся ли спуски к минимуму, зависит от функции и выбора нулевого приближения.

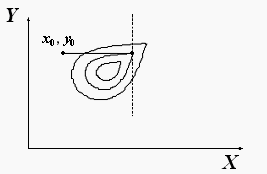
Геометрическая иллюстрация будет следующей: будем двигаться по выбранному направлению, по некоторой прямой в плоскости XY.

В тех участках, где прямая пересекает линии уровня, мы при движении переходим от одной линии уровня к другой, так что при этом движении функция меняется. В зависимости от направления движения функция возрастает или убывает. Только в той точке, где прямая касается линии уровня, функция имеет экстремум вдоль этого направления. Найдя такую точку, мы завершаем в ней спуск по первому направлению и должны начать спуск по второму.

Пусть линии уровня образуют истинный овраг. Тогда возможен случай, когда спуск по одной координате приводит нас на "дно оврага", а любое движение по следующей координате (пунктирная линия) ведет нас на подъем. Никакой дальнейший спуск по координатам невозможен, хотя минимум еще не достигнут. Тогда такой процесс спуска по координатам не сходится к минимуму.

Рельеф функции

Понятие "рельеф функции" удобно рассмотреть на примере функции двух переменных z=F(x, y). Эта функция описывает некоторую поверхность в трехмерном пространстве с координатами x, y, z. Задача F(x, y)->min означает поиск низшей точки этой поверхности.

Как в топографии, изобразим рельеф этой поверхности линиями уровня. Проведем равностоящие плоскости z=const и найдем линии их пересечения с поверхностью F(x, y). Проекции этих линий на плоскость XY называют линиями уровня. Направление убывания функции будем указывать штрихами рядом с линиями уровня. По виду линий уровня условно выделим три типа рельефа: котловинный, овражный и неупорядоченный.

При котловинном рельефе линии уровня похожи на эллипсы.
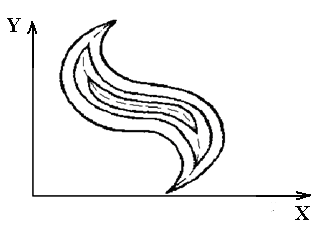
Овражный тип рельефа. Если линии уровня кусочно-гладкие, то выделим на каждом из них точку излома. Геометрическое место излома назовем истинным оврагом, если угол направлен в сторону возрастания функции, и гребнем, – если в сторону убывания.

Существуют, так называемые неупорядоченные типы рельефа. Такие рельефы характеризуется наличием многих максимумов и минимумов.

10. Метод оврагов Случайный поиск

Выберем произвольную точку и спустимся из нее (например, по координатам), делая не очень много шагов, то есть, не требуя высокой точности. Конечную точку спуска обозначим . Если рельеф овражный, эта точка окажется вблизи дна оврага.

Теперь выберем другую точку не слишком далеко от первой. Из нее также сделаем спуск и попадем в некоторую точку . Эта точка тоже лежит вблизи дна оврага. Проведем через точку и на дне оврага прямую – приблизительную линию дна оврага, передвинемся по этой линии в сторону убывания функции и выберем новую точку на этой прямой, на расстоянии h от точки r₁. Величина h называется овражным шагом и для каждой функции подбирается в ходе расчета.

Дно оврага не является отрезком прямой, поэтому точка на самом деле лежит не на дне оврага, а на его склоне. Из этой точки снова спустимся на дно и попадем в некоторую точку . Затем соединим точки и прямой, наметим новую линию дна оврага и сделаем новый шаг по оврагу. Продолжим процесс до тех пор, пока значения функции на дне оврага, то есть в точках убывают.

В случае, когда процесс надо прекратить и точку не использовать. Метод оврагов рассчитан на то, чтобы пройти вдоль оврага и выйти в котловину около минимума. В этой котловине значение минимума лучше уточнять другими методами.