16. Поиск оптимума в задачах с ограничениями. Метод факторов.

Своеобразным и очень эффективным методом штрафов является метод факторов (или множителей), который основан на штрафе типа "квадрат срезки" для ограничений-неравенств. Такой штраф определяется следующим образом , где срезка t определяется так: 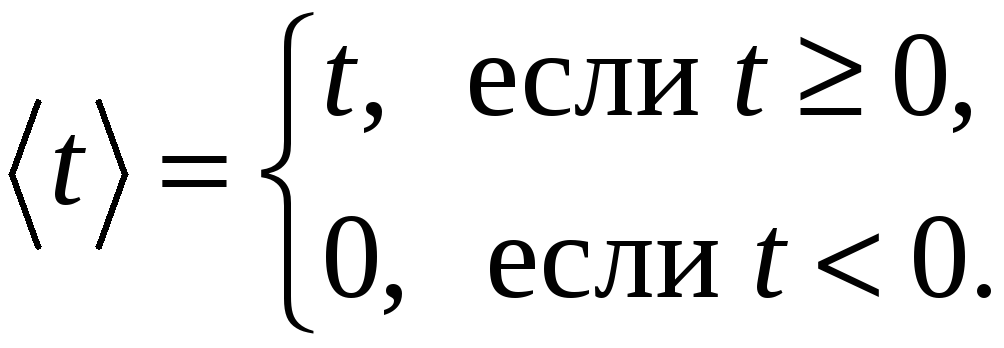Этот штраф внешний и стационарные точки функции Q(x,R) могут оказаться недопустимыми. С другой стороны, недопустимые точки не создают в данном случае дополнительных сложностей по сравнению с допустимыми. Различие между ними состоит лишь в том, что в допустимых точках штраф равен нулю. В методе факторов на каждой итерации производится безусловная минимизация функции , где R - постоянный весовой коэффициент, а угловые скобки обозначают операцию срезки. Параметры (факторы) σ_j и ì_k осуществляют сдвиг штрафных слагаемых. Компоненты векторов σ и ì меняются по ходу вычислений, однако в процессе решения каждой вспомогательной безусловной задачи оба эти вектора остаются постоянными. Начальные значения факторов σ и ì можно выбрать нулевыми. Обозначим через x^m точку минимума функции , используемой на m-ой итерации. При переходе к (m+1)-й итерации факторы пересчитываются по формулам , . Формулы пересчета таковы, что в результате сдвига при переходе к новой подзадаче штраф за нарушение ограничений возрастает, и вследствие этого точки x^m приближаются к допустимой области. Для контроля сходимости метода используют последовательности x^m, σ^m , ì^m , f(x^m ), g(x^m ), h(x^m). Прекращение основного процесса происходит, когда члены, по крайней мере, одной из этих последовательностей, перестают изменяться при пересчете факторов и последующей безусловной минимизации. Заметим, что величина положительного параметра R влияет на свойства метода, но конструктивного алгоритма его выбора не существует.

17. Линейное программирование. Постановка задач. Основная (каноническая) задача и сведение к ней произвольной задачи.

Постановка задачи. Основная задача линейного программирования состоит в следующем. Задана система

линейных алгебраических уравнений с неизвестными и линейная форма относительно этих же неизвестных: . Требуется среди всех неотрицательных решений данной системы выбрать такое, при котором форма F принимает наименьшее значение, т.е. минимизируется. Данная система называется системой ограничений решаемой задачи, а равенства системы называются ограничениями-равенствами. Также в задаче есть ограничения-неравенства

При решении данной задачи всякое неотрицательное решение системы назовем допустимым. Допустимое решение также называют планом задачи линейного программирования. А допустимое решение Для основной системы есть ряд ограничений. Задача имеет смысл лишь в том случае, когда система совместна, т.е. когда ранги основной и расширенной матриц системы совпадают. Этот общий ранг r не может превосходить числа неизвестных. При решение системы единственно. Если это решение допустимо, то оно является оптимальным, так как никаких других решений вообще нет. Если единственное решение не является допустимым, то задача не имеет решения.

Таким образом, будем рассматривать случай .

Каждую задача линейного программирования можно свести к форме основной задачи. Для этого нужно: 1. Уметь сводить задачу максимизации к задаче минимизации.

2. Уметь переходить от ограничений, заданных в виде неравенств, к эквивалентным им ограничениям-равенствам.

1. Форма F достигает наибольшей величины при тех же самых значениях неизвестных , при которых форма F₁=-F достигает наименьшей величины. Следовательно, максимизация формы F равносильна минимизации формы F₁=-F. Тем самым задача максимизации сводится к задаче минимизации.

2. Допустим теперь, что среди ограничений задачи имеется некоторое неравенство. Его всегда можно записать в виде .(*)

Введем новую, добавочную, неизвестную, связанную с неизвестными уравнением.(**)Т.е. если положительно, то неравенство(*) выполняется. Если система неотрицательных значений удовлетворяет уравнению(**), то система удовлетворяет неравенству (*). Также верно обратное утверждение, если величины неотрицательны и удовлетворяют неравенству (*), то величина окажется Получаем, что ограничение-наравенство (*) эквивалентно ограничению-равенству (**), что требовалось сделать. Число добавочных неизвестных равно числу ограничений-неравенств в исходной задаче.