
- •Основные понятия
- •Дифференциальные уравнения
- •Обыкновенные дифференциальные уравнения Уравнения с
- •Графичес- Аналити- Прибли- Численное Численное
- •Метод Решение Методы
- •3.2. Методы решения. Общие положения
- •3.3. Задача Коши. Общие замечания
- •3.4. Метод Пикара
- •Так как должны выполняться условия (3.21), (3.22) можно записать в виде
- •3.6. Метод Эйлера
- •Аналогично определяем отрезки , , …
- •Так как искомую точку находим как точку пересечения прямой с ординатой , то можно записать:
- •Метод согласуется с рядом Тейлора вплоть до членов степени .
- •На рис. 11 видно, что расхождение этого метода значительно меньше расхождения обычного метода Эйлера, равного .
- •3.7. Метод РунгеКутта
- •3.8. Метод Адамса
- •(К выводу формулы метода Адамса)
Аналогично определяем отрезки , , …
Как видно из рис.
9, решение по методу Эйлера представляет
собой ломаную
![]()
![]()
![]()
![]() . . . (так называемая ломаная
Эйлера). Звенья
этой ломаной в каждой вершине
. . . (так называемая ломаная
Эйлера). Звенья
этой ломаной в каждой вершине
![]() имеют направление
имеют направление
![]() ,
совпадающее с направлением интегральной
кривой уравнения (3.40), проходящей через
точку
,
совпадающее с направлением интегральной
кривой уравнения (3.40), проходящей через
точку
![]() .
.
Из рис. 9 также
видно, в методе Эйлера есть только
единственное точное решение
это
![]() .
Для
.
Для
![]() расхождение
расхождение
![]() равняется
равняется
![]() (
(![]()
точное решение для
точное решение для
![]() ),
для
),
для
![]() расхождение
расхождение
![]() составит
составит
![]() (точка
(точка
![]() на рис. 9 не обозначена), таким образом,
расхождение с каждым шагом накапливается.
на рис. 9 не обозначена), таким образом,
расхождение с каждым шагом накапливается.
 y
y
![]()

![]()



![]()

![]()
![]()



![]()

![]()





![]()





![]()
![]()




h h h

О
![]()
![]()
![]()
![]()
![]()
Рис. 9
Замечания к методу Эйлера.
Замечание 1. Метод Эйлера и его модификации являются простейшими представителями конечно-разностных методов (шаговых методов) для приближенного решения обыкновенных дифференциальных уравнений.
Замечание
2. Доказывается
[12], что если правая часть
![]() уравнения (3.40) непрерывна, то
последовательность ломаных Эйлера при
уравнения (3.40) непрерывна, то
последовательность ломаных Эйлера при
![]() на достаточно малом отрезке
на достаточно малом отрезке
![]() равномерно стремится к искомой
интегральной кривой
равномерно стремится к искомой
интегральной кривой
![]() .
.
Замечание
3. Метод Эйлера
имеет малую точность: с разложением
Тейлора согласуется вплоть до
![]() ,
поэтому для получения большей точности
необходимо уменьшить шаг, но это приводит
к увеличению объема вычислений.
,
поэтому для получения большей точности
необходимо уменьшить шаг, но это приводит
к увеличению объема вычислений.
Замечание 4. Ошибки систематически накапливаются.
Замечание 5. Метод позволяет начать счет при i = 0 по известным начальным значениям.
Замечание 6. В этом методе можно изменить шаг в любой точке в процессе счета, что позволяет строить численные алгоритмы с автоматическим выбором шага.
Замечание
7. Как мы уже
отмечали, на рис. 9 кривая
![]() ,
проходящая через точку
,
проходящая через точку
![]() ,
есть точное решение задачи Коши. И
касательную
,
есть точное решение задачи Коши. И
касательную
![]() мы проводим именно к этой кривой. Точка
же
мы проводим именно к этой кривой. Точка
же
![]() ,
полученная в результате решения методом
Эйлера, из-за его погрешности принадлежит
уже другой
интегральной
кривой (чтобы не насыщать рис. 9
дополнительными деталями, эта кривая
не обозначена). Поэтому касательная
,
полученная в результате решения методом
Эйлера, из-за его погрешности принадлежит
уже другой
интегральной
кривой (чтобы не насыщать рис. 9
дополнительными деталями, эта кривая
не обозначена). Поэтому касательная
![]() в точке
в точке
![]() проводится уже к этой новой кривой.
Таким образом, погрешность метода Эйлера
приводит к тому, что на каждом шаге
решение переходит на другую интегральную
кривую.
проводится уже к этой новой кривой.
Таким образом, погрешность метода Эйлера
приводит к тому, что на каждом шаге
решение переходит на другую интегральную
кривую.
Замечание 8. Метод Эйлера легко распространяется на системы дифференциальных уравнений.
Пример 13. Методом Эйлера проинтегрировать уравнение
![]()
на отрезке [0; 0.1] с
шагом h
= 0,05, при начальном условии
![]() .
.
Решение.
Определяем значение производной при
![]() = 0:
= 0:
![]() .
.
Теперь по формуле
(3.44) вычисляем
![]() при х
= 0,05
при х
= 0,05
![]()
Вычисляем производную
при
![]() =
=
![]() + h
=0 + 0,05 = 0,05:
+ h
=0 + 0,05 = 0,05:
![]()
Искомое значение
функции при
![]() =
=
![]() + h
= 0,05 + 0,05 = 0,1 будет
+ h
= 0,05 + 0,05 = 0,1 будет
![]() = 1,1050
= 1,1050
б) исправленный метод Эйлера. Сначала дадим геометрическую интерпретацию данного метода (рис. 10).
1. Точно так же, как
и в обычном методе Эйлера, через точку
![]() проводим касательную
проводим касательную
![]() с угловым коэффициентом
с угловым коэффициентом
![]() и находим точку
и находим точку
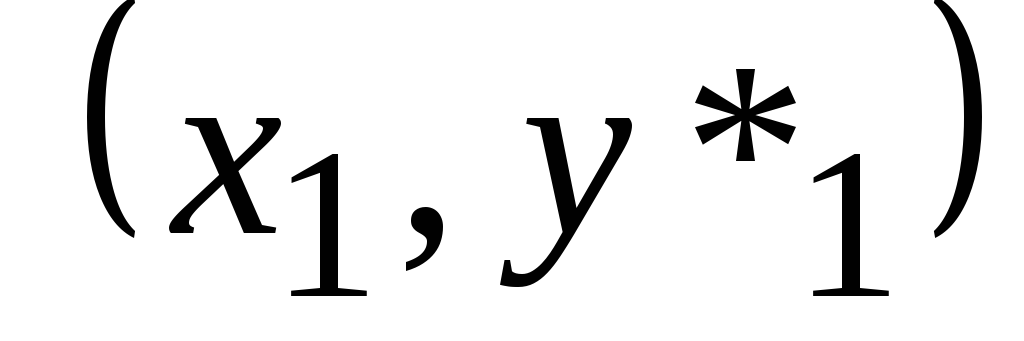 .
.
2. К кривой![]() ,
проходящей через точку
,
проходящей через точку
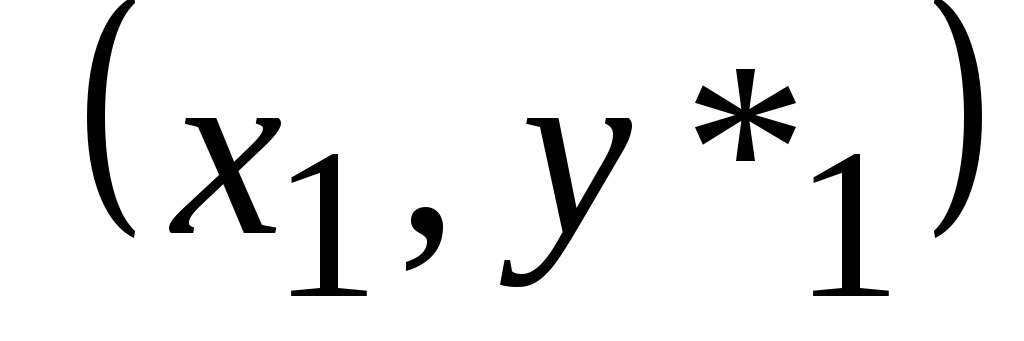 ,
проводим касательную
,
проводим касательную
![]() с угловым коэффициентом
с угловым коэффициентом
![]() .
.
3. Находим
среднее значение угловых коэффициентов
касательных
![]() и
и
![]() :
:
![]() .
.
4. Проводим через
точку
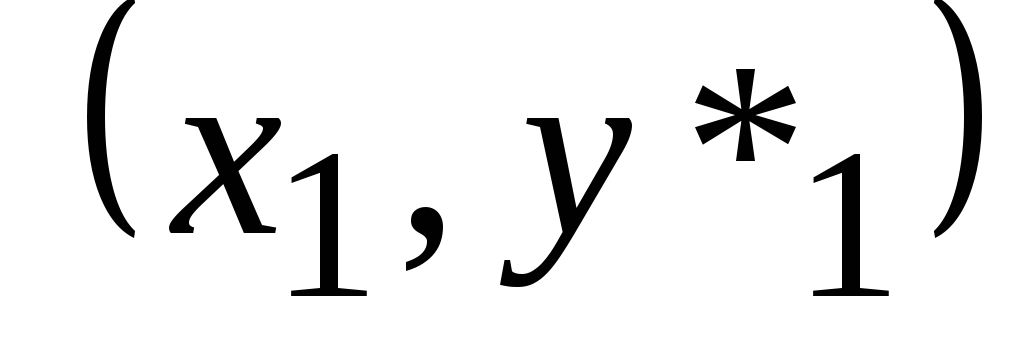 прямую
прямую
![]() с угловым коэффициентом
с угловым коэффициентом
![]() .
.
5. Через точку
![]() проводим прямую
проводим прямую
![]() ,
параллельную
,
параллельную
![]() .
.
6. Находим точку
пересечения прямой
![]() ,
с прямой х
=
,
с прямой х
=
![]() ,
т.е. точку
,
т.е. точку
![]() ;
ординату
;
ординату
![]() этой точки и принимаем за решение
уравнения (3.40) при х
=
этой точки и принимаем за решение
уравнения (3.40) при х
=
![]() =
=
![]() .
.
7. Таким же способом
получаем решения в точках
![]() ,
,
![]() ,
. . .
,
. . .
Основываясь на геометрической интерпретации, получим формулу исправленного метода Эйлера.
Угловые коэффициенты
касательных
![]() и
и
![]() соответственно равны:
соответственно равны:
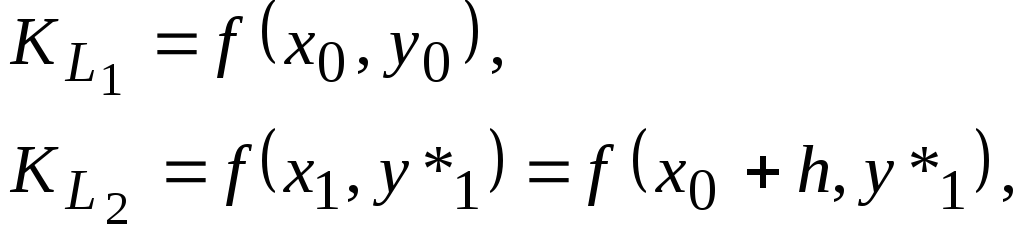 (3.47)
(3.47)
где
![]() ,
поэтому
,
поэтому
![]() .
(3.48)
.
(3.48)
На основании (3.47)
и (3.48) получаем тангенс угла наклона
прямой
![]() (а значит, и прямой
(а значит, и прямой
![]() ,
так как она по построению параллельна
прямой
,
так как она по построению параллельна
прямой
![]() ):
):
![]() .
.
