Численные методы
ЛЕКЦИЯ 6 – 7
ПОНЯТИЕ УСТОЙЧИВОСТИ И СХОДИМОСТИ.
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Лекции 6 − 7. Понятие устойчивости и сходимости.
Численные методы решении
обыкновенных дифференциальных уравнений
Основные понятия
Изложение материала предположении, что читатель знаком с основами теории дифференциальных уравнений. Здесь же мы напомним лишь некоторые сведения из курса дифференциальных уравнений, которые будут нам необходимы в дальнейшем.
Как известно, дифференциальное уравнение уравнение, содержащее искомую функцию, ее производные различных порядков и независимые переменные. Дифференциальные уравнения делятся на обыкновенные дифференциальные уравнения, содержащие производные одной или нескольких функций от одной независимой переменной, и уравнения с частными производными (или уравнения в частных производных), содержащие частные производные функций нескольких независимых переменных. Данная глава посвящена методам решения обыкновенных дифференциальных уравнений.
Обыкновенные дифференциальные уравнения можно записать в виде
(3.1)
,
,
где x – независимая переменная.
К обыкновенным дифференциальным уравнениям относят и дифференциальные уравнения с параметрами, когда искомая функция зависит от нескольких аргументов, но производные, участвующие в уравнении, берутся лишь по одному из аргументов, например,
.
Для краткости обыкновенное дифференциальное уравнение называют обычно «дифференциальным уравнением».
Порядком дифференциального уравнения называется наивысший порядок n входящей в уравнение (3.1) производной. В частности, уравнения первого и второго порядков в форме (3.1) запишутся так:
,
.
Если из общей записи дифференциального уравнения (3.1) удается выразить старшую производную в явном виде, например,
,
,
то такая форма записи называется дифференциальным уравнением в нормальной форме (или уравнением, разрешенным относительно старшей производной).
Линейным дифференциальным уравнением называется уравнение вида
,
(3.2)
где
искомая функция;
ее производные;
,
…,
,
коэффициенты;
свободный член.
В уравнение (3.2) искомая функция и ее производные входят в первой степени, т.е. линейно (поэтому оно и называется линейным).
Если
= 0, то уравнение (3.2) называется однородным.
Если
,
то уравнение (3.2)
неоднородное.
Пример линейного дифференциального уравнения:
.
Решением
дифференциального уравнения (3.1)
называется всякая действительная или
комплексная функция
,
которая после ее подстановки в уравнение
превращает его в тождество. Функция
должна обладать производными всех
порядков до наивысшего порядка уравнения
включительно. Процесс нахождения решения
называется разрешением
(или интегрированием)
дифференциального
уравнения.
Соотношение
,
(3.3)
содержащее n
произвольных постоянных
,
называется общим
решением
обыкновенного дифференциального
уравнения n-го
порядка (3.1), если при соответствующем
выборе постоянных
получается решение с любыми начальными
данными.
Частное
решение дифференциального
уравнения получается из общего, если
произвольным постоянным
придать определенные значения.
Например,
дифференциальное уравнение первого
порядка
,
т. е.
,
имеет решением
,
где C
> 0 – произвольная постоянная. При
различных значениях постоянной C
получается семейство окружностей (рис.
3). Выбор начального значения
при
(обычно
)
позволяет выделить из этого семейства
одну определенную кривую, т.е. найти
частное решение (на рис. 3 выделена
окружность, которой принадлежит точка
A,
имеющая координаты
и
).
Для уравнений
высших порядков геометрическая
интерпретация более сложная. Через
каждую точку в области решения уравнения
при
проходит не одна интегральная кривая.
Поэтому для выделения частного решения
из общего нужно задавать столько
дополнительных условий, сколько
произвольных постоянных в общем решении,
т.е. каков порядок уравнения. Следовательно,
для уравнения второго порядка нужно
задать два дополнительных условия,
благодаря которым можно найти значения
двух произвольных постоянных.
В зависимости от способа задания дополнительных условий для получения частного решения дифференциального уравнения существуют два различных типа задач: задача Коши и краевая задача. В качестве дополнительных условий могут задаваться значения искомой функции и ее производных при некоторых значениях независимой переменной, т.е. в некоторых точках.
Если эти условия
задаются в одной точке, то такая задача
называется задачей
Коши.
Дополнительные условия в задаче Коши
называются начальными
условиями, а
точка
,
в которой они задаются
начальной
точкой.
Примеры:
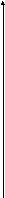
y
A
x
