19

Численные методы

ЛЕКЦИЯ 5

ЧИСЛЕННОЕ ДИФФИРИНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ

Лекция 5. Численное дифференцирование и интегрирование

2.1. Постановка задачи и оценка точности

численного дифференцирования

Численное дифференцирование – это нахождение производной функции численными методами. Численное дифференцирование используется в тех случаях, когда методы дифференциального исчисления неприменимы (функция задана таблично) или их применение вызывает значительные трудности (функция имеет сложное аналитическое выражение).

Рассмотрим методы численного дифференцирования.

Напоминаем, что производная есть основное понятие дифференциального исчисления, которая характеризует скорость изменения функции при изменении аргумента x, и определяется как предел отношения приращения функции к приращению аргумента при стремлении к нулю:

. (2.1)

При вычислении производных обычно используют готовые формулы. Но если функция задана таблично, производную находят, опираясь на формулу (2.1). В этом случае приращение аргумента полагают равным некоторому конечному числу, и значение производной вычисляют через приближенное равенство

. (2.2)

Соотношение (2.2) называют аппроксимацией производной с помощью отношения конечных разностей.

Пусть функция задана в табличном виде. Шаг – разность между соседними значениями аргумента – постоянный и равен h. Рассмотрим аппроксимацию производной для заданной функции. В зависимости от способа вычисления конечных разностей получим разные формулы для вычисления производной в одной и той же точке.

Если будем вычислять производную через левые разности, то есть и , то

. (2.3)

Формула для вычисления производной через правые разности (; ) будет такая:

. (2.4)

Если использовать центральные разности (; ), формулой для вычисления значения производной будет выражение

. (2.5)

По формуле (2.2) можно найти приближенные значения производных любого порядка. В частности, выражение для вычисления второй производной будет следующим:

. (2.6)

Однако при таком способе вычислений вопрос о точности вычислений остается открытым. Поэтому сейчас остановимся на вопросах оценки погрешности численного дифференцирования.

Выше было отмечено, что при приближении функции некоторой функцией появляется остаток (погрешность аппроксимации) (1.2), который выражается как , так что

. (2.7)

Если за функцию взять частичную сумму ряда, то определяется остаточным членом ряда. Функция может быть использована для приближенного вычисления производной функции . Если дифференцировать равенство (2.7) необходимое число раз, можно найти значения производных

, , . . .

и в качестве приближенного значения производной порядка k функции можно принять соответствующее значение производной функции , т.е.:

.

Величина , определяющая отклонение приближенного значения производной от ее истинного значения, называется погрешностью аппроксимации производной.

При численном дифференцировании функции, заданной в виде таблицы с шагом h, погрешность зависит от h, и ее записывают в виде , где показатель степени k называется порядком погрешности аппроксимации. В выражении предполагается, что значение шага h по модулю меньше единицы.

Чтобы проиллюстрировать оценку погрешности, рассмотрим ряд Тейлора

. (2.8)

Если функция задана таблично с постоянным шагом h, то .

Теперь запишем (2.8) при и с точностью до членов первого порядка h:

;

отсюда можно найти значение производной в точке :

.

Сравнивая полученное выражение с (2.3), можно сделать вывод, что производная, вычисленная через левые разности, имеет первый порядок погрешности аппроксимации (k = 1). Если записать ряд Тейлора при , можно получить аппроксимацию первой производной с помощью правых разностей, она также будет иметь первый порядок погрешности, т.е.

.

Теперь оценим погрешности производных (2.5) и (2.6). Для этого запишем (2.8) при и соответственно:

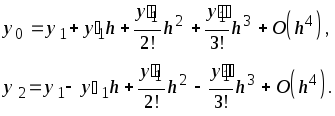(2.9)

Вычитая эти равенства одно из другого, после преобразований получим

.

Таким образом, аппроксимация производной с помощью центральных разностей имеет второй порядок погрешности аппроксимации.

Складывая равенства (2.9), находим оценку погрешности для производной второго порядка (2.6):

,

которая также имеет второй порядок.

Аналогично можно получить аппроксимации производных более высоких порядков и оценку их погрешностей.

Необходимо отметить, что для хорошей аппроксимации производной нужно использовать значения функции во многих узлах. В качестве примера оценим погрешности аппроксимации производных и , вычисленных при помощи значений функции в трех узлах. (К вычисленным таким образом производным и обращаемся потому, что они применяются в некоторых численных методах решения обыкновенных дифференциальных уравнений.) Запишем (2.8) при и соответственно:

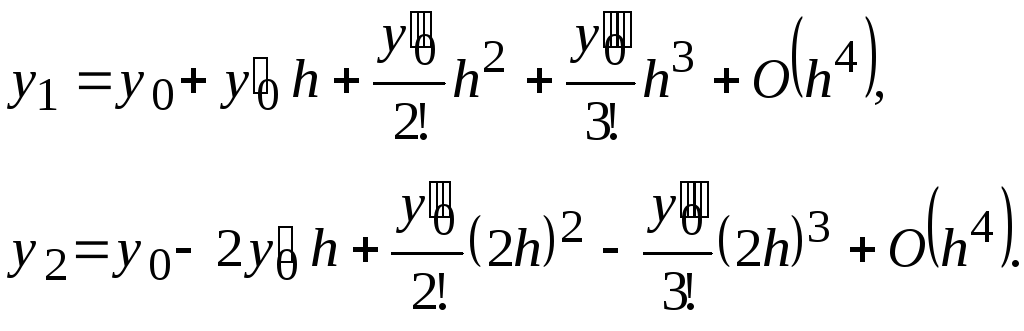
Из этих равенств получаем:

. (2.10)

Аналогично можно получить выражение для вычисления :

, . (2.11)

Как видим, для обеих производных получается второй порядок погрешности аппроксимации. Заметим, применение формул (2.10) и (2.11) предполагает, что функция достаточная гладкая в окрестностях точек и .

Основными источниками погрешности при численном дифференцировании являются: 1) погрешность аппроксимации, 2) неточность значений функции в узлах таблицы и 3) погрешности округлений при проведении расчетов.

Выше была рассмотрена погрешность аппроксимации производной, которая есть отклонение приближенного значения производной от ее истинного значения и возникает из-за того, что в формулах учитывается ограниченное число членов, зависящих от величины шага h. Эта погрешность, записываемая обычно в виде , при уменьшении шага h , как правило, уменьшается.

Погрешность округления, в отличие от погрешности аппроксимации, с уменьшением шага h возрастает. В результате чего суммарная погрешность численного дифференцирования может убывать лишь до некоторого предельного значения, после чего дальнейшее уменьшение шага не повысит точности результатов.

Для достижения оптимальной точности проводят регуляризацию процедуры численного дифференцирования. Одним из способов регуляризации является выбор шага h так, чтобы выполнялось условие , где – некоторое малое число. Это исключает вычитание близких по величине чисел и в последующем деление приращения функции на малое число h, что обычно приводит к увеличению погрешности. Другой способ регуляризации – сглаживание табличных значений функции подбором некоторой гладкой аппроксимирующей функции, например многочлена.

2.2. Применение интерполяционных формул для численного дифференцирования

Известно, что хорошая аппроксимация производной достигается при использовании значений функции во многих узлах (заметим, что в формуле (2.2), это не предусмотрено). Задачу уменьшения погрешности аппроксимации можно решить применением интерполяционных формул.

Если функция дана в виде таблицы значений, соответствующих равноотстоящим значениям независимой переменной, то ее можно представить при помощи одной из интерполяционных формул, содержащих разности, вроде формул Ньютона, Бесселя или Стирлинга. В этом случае и значения производных даются формулами, содержащими разности. Если же значения функции даны для неравноотстоящих значений независимой переменной, то мы должны представить функцию при помощи формулы Лагранжа. Выбор между формулами с разностями производится на тех же основаниях, что и при интерполировании. Так если мы ищем производную в точке, близкой к началу ряда табличных значений, нужно пользоваться первой формулой Ньютона. Когда ищут производную в точке, близкой к концу таблицы, то применяют вторую формулу Ньютона. Для точек, близких к середине таблицы, пользуются формулой центральных разностей Стирлинга или Бесселя.

Для рассмотрения численного дифференцирования с использованием значений функции во многих узлах обратимся к первой интерполяционной формуле Ньютона для функций с равноотстоящими узлами (1.14).

В этой формуле переменная величина , где и h постоянны. Поэтому, учитывая, что ,

.

Отсюда, принимая во внимание, что

;

;

;

. . . . . . . . . . . . . . ,

получаем

. (2.12)

Аналогично

. (2.13)

Продолжая дифференцировать, можно найти производные третьего и более высокого порядков.

На примере применения первой интерполяционной формулы Ньютона мы рассмотрели, как вычисляются производные функции, заданной таблично, используя конечные разности с равномерным расположением узлов. Оценку точности применения интерполяционных формул мы рассмотрели в главе 1. Если использовать интерполяционную формулу Лагранжа, то аппроксимацию производных можно осуществлять непосредственно через значения функции в узлах (выражения для вычисления производных не приводятся). Заметим, что формулу Лагранжа можно применять для аппроксимации производных и в случае произвольного расположения узлов.

2.3. Метод Рунге-Ромберга

Необходимо отметить, что при нахождении производных точность вычислений быстро понижается. Так, если значения функции заданы с 10 знаками после запятой и каждая из последующих разностей имеет на одну значащую цифру меньше, то производные первого, второго и третьего порядков имеют соответственно 9, 8 и 7 верных знаков после запятой. Поэтому используются методы уточнения решения. Наиболее простым и эффективным способом при фиксированном числе узлов является метод Рунге-Ромберга [9]. Суть этого метода следующая.

Предполагается, что аппроксимация производной в виде конечно-разностной функции на равномерной сетке с шагом h уже построена.

Пусть R – остаточный член или погрешность аппроксимации:

,

где – главный член погрешности аппроксимации.

Запишем выражения для аппроксимации производной в точке x при шаге h и в той же точке при шаге :

, (2.14)

.

Из этих выражений можно найти выражение для главного члена погрешности аппроксимации производной:

.

Подставив полученное выражение в равенство (2.14) получаем формулу Рунге:

. (2.15)

Данная формула позволяет для двух расчетов значений производной и (то есть с шагами h и kh) с порядком точности p найти ее уточненное значение с точностью p + 1 .

Пример 5 [15]. Вычислить производную функции для x = 1.

Решение. Так как , поэтому мы можем вычислить точное значение производной: .

Теперь найдем значение производной численно. Для этого составим таблицу значений функции :

x	0,8	0,9	1,0
y	0,512	0,729	1,0

Аппроксимацию производной выполним с помощью левых разностей, имеющих первый порядок (p = 1). Пусть h = 0.1 и k =2, тогда kh = 0.2. С этими исходными получаем:

,

.

По формуле Рунге (2.15) уточним значение производной:

.

Из сравнения результатов можно сделать вывод, что формула Рунге дает более точное значение производной.

В общем случае порядок точности аппроксимации по формуле Рунге увеличивается на единицу.

Выше был рассмотрен метод уточнения решения при двух значениях шага. Теперь предположим, что расчеты проводятся с шагами . В этом случае уточненное решение выполняют по формуле Ромберга:

+

.

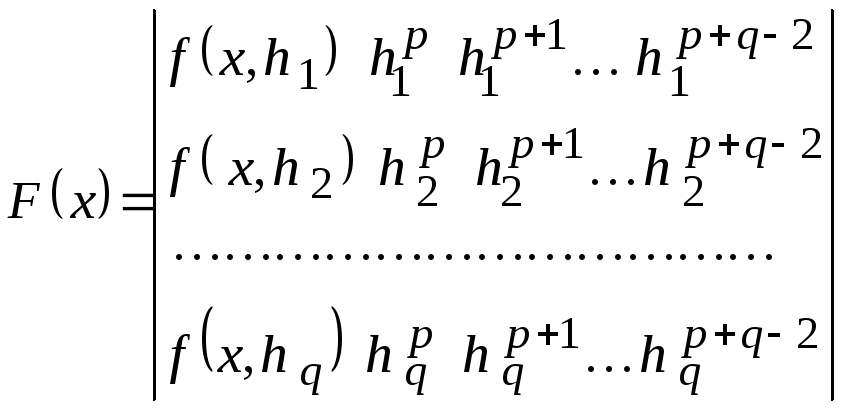
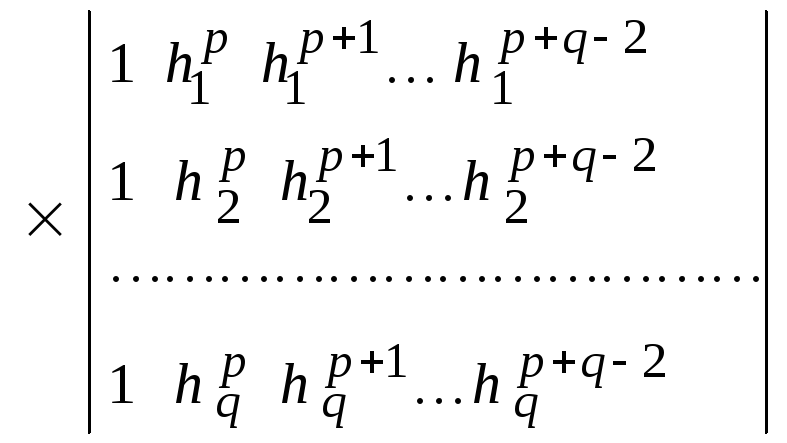Использование данной формулы приводит к возрастанию порядка точности на q – 1. Необходимо отметить, что для успешного применения уточнения исходная функция должна иметь непрерывные производные достаточно высокого порядка.

В завершение вопроса численного дифференцирования рассмотрим трудности, возникающие при обработке экспериментальных данных [10].

Первая трудность проистекает из самой природы табулированной информации, полученной экспериментальным путем, так как в каждом экспериментальном измерении в большей или меньшей степени всегда присутствуют шумы или погрешности экспериментов. Если эти данные продифференцировать, влияние погрешности существенно возрастает.

Вторая трудность, связанная с численным дифференцированием, проиллюстрирована на рис. 2, откуда видно, что интерполяционный многочлен g (x) хотя и может адекватно описать табулированную функцию f (x), его производные высоких порядков могут совершенно отличаться от таких же производных табулированной функции (на рис. 2 это можно видеть, если сравнить наклоны и кривизны двух кривых).

y f (x)

g(x)

x

Рис. 2. К вопросу о точности численного дифференцирования