4.4. Метод Симпсона (метод парабол).

Погрешность численного интегрирования определяется шагом разбиения, поэтому, уменьшая его, можно добиться большей точности. Но увеличивать число точек не всегда возможно. Например, если функция задана в табличном виде, приходится ограничиться, как правило, данным множеством точек. В этом случае повышение точности может быть достигнуто за счет повышения степени используемых интерполяционных многочленов. Рассмотрим один из таких способов численного интегрирования, а именно метод Симпсона (Т.Симпсон  английский математик, член Лондонского королевского общества, профессор Вулиджской военной академии. По профессии он был ткачом шелковых тканей, а математику изучил самостоятельно. Является одним из основоположников теории ошибок. Формулу приближенного интегрирования вывел в 1743 г., вернее, эта формула фактически была им лишь вновь открыта. Он не знал, что ее содержание до него было известно Торичелли (1644), Грегори (1668), Ньютону (1676) и Котесу (1722)). Заметим, что этот метод является также и одним из наиболее применяемых методов численного интегрирования.

Изложим один из способов вывода формулы Симпсона.

Так же, как и в методе трапеций, в методе Симпсона интегрирование проводится разбиением общего интервала интегрирования на множество более мелких отрезков, но в данном методе отрезок интегрирования делят на четное число n равных частей с шагом h, и для вычисления площади через три последовательные ординаты проводится парабола

. (1)

Для упрощения ось ординат направим вдоль ординаты , поскольку площадь трапеции от этого не изменится. Тогда , , (рис. 21). Подставив эти значения в выражение (1), получим систему уравнений:

;

;

.

Решив ее, найдем:

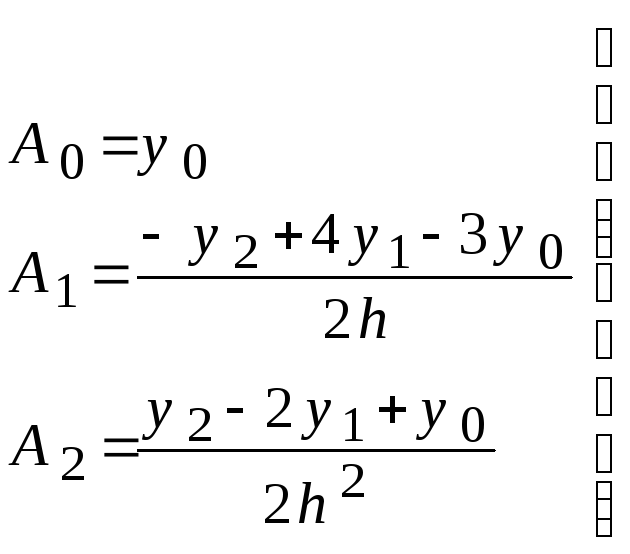(2)

Площадь криволинейной трапеции, ограниченная сверху параболой, равна

,

то есть (с учетом выражений (6.9))

.

Аналогично

;

. . . . . . . . . . . .

.

Просуммировав полученные значения площадей, получаем соотношение, которое принимается в качестве значения определенного интеграла (числа, стоящие перед значениями функции , , …, называются весовыми коэффициентами):

. (3)

Полученное выражение есть формула Симпсона. В литературе встречается и другое название  первая формула Симпсона. Дело в том, что для случая, когда парабола проводится через четыре последовательные ординаты  , была выведена вторая формула Симпсона. Но

оказалось, что вторая формула менее проста и менее точна, чем первая, поэтому в вычислениях не нашла применения в общем виде (поэтому полное выражение для второй формулы здесь не приводим). Но в тех случаях, когда количество промежутков нечетно (а для первой формулы Симпсона, как мы знаем, необходимо иметь четное число промежутков), для первых трех промежутков применяют формулу, использующую параболу третьей степени, то есть частный случай второй формулы Симпсона, которая еще известна как формула Симпсона трех восьмых:

.

Оценки показывают, что погрешность метода Симпсона и формулы (1) (п. 4.3) имеют одинаковый порядок. Разница же между этими методами заключается в том, что указанная формула (1) требует двукратного вычисления интеграла разными методами. Кроме того, для метода Симпсона нужно почти вдвое меньше табличных значений функции, поскольку для метода прямоугольников нужны дополнительные данные в полуцелых точках.

В приложении дан пример решения задачи с применением метода Симпсона.

Численное интегрирование

Погрешность метода при интегрировании функции f на отрезке [;] имеет величину:

R =, где [;]. (5.32)

Из формулы (5.32) видно, что при <0 формула (5.27) дает значение интеграла с избытком, а при >0 – с недостатком.

При распространении оценки (5.32) на весь отрезок интегрирования [a; b] (т.е. на все п частичных отрезков) получается формула:

= , где [a; b].

Учитывая, что hn = a – b, окончательный вид формулы для оценки погрешности метода трапеций будет такой:

= , (5.33)

где

.

Пример 5. Вычислить интеграл по формуле трапеций, разделив отрезок [a; b] на 10 равных частей, и оценить погрешность вычислений.

Чтобы оценить ошибку метода, находим вторую производную подынтегральной функции:

.

На отрезке [0; 1] всюду положительна, причем ее значение ограничено сверху <3,3. Таким образом, используя формулу (5.33) (a=0; b= 1; h=0,1), имеем:

| R |< = 0,00275.

Итак, приняв на заданном участке интегрирования п = 10, мы сможем получить интеграл от заданной функции с погрешностью, не превышающей 0,003.

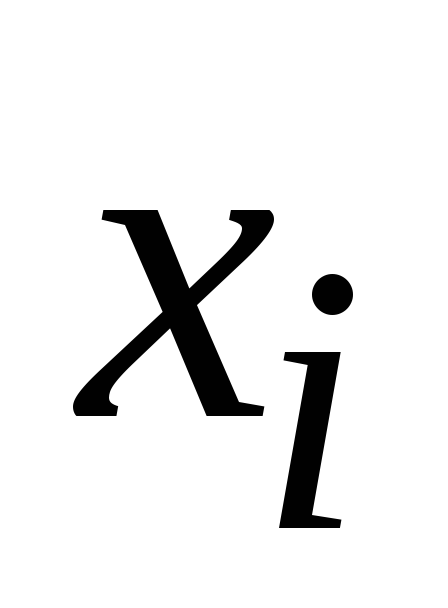
	/2 (i = 0, 10)	(i = 1, 2, ...,9)
0	0	0,0009983
0,1		0,0079468
0,2		0,0265968
0,3		0,0623069
0,4		0,1198564
0,5		0,2032712
0,6		0,3156667
0,7		0,4591078
0,8		0,6344948
0,9
1,0	0,4207355
	0,4207355	1,8302459

Оценка остаточного члена формулы Симпсона дается формулой

= , где [a; b]

или

= , (5.36)

где .

Существует простой практический прием, позволяющий прогнозировать требуемое число отрезков разбиения по заданной точности .

Пусть задана предельная допустимая погрешность интегрирования . Желая иметь , с учетом оценки (5.36), достаточно потребовать:

,

откуда получаем

, т.е. . (5.37)